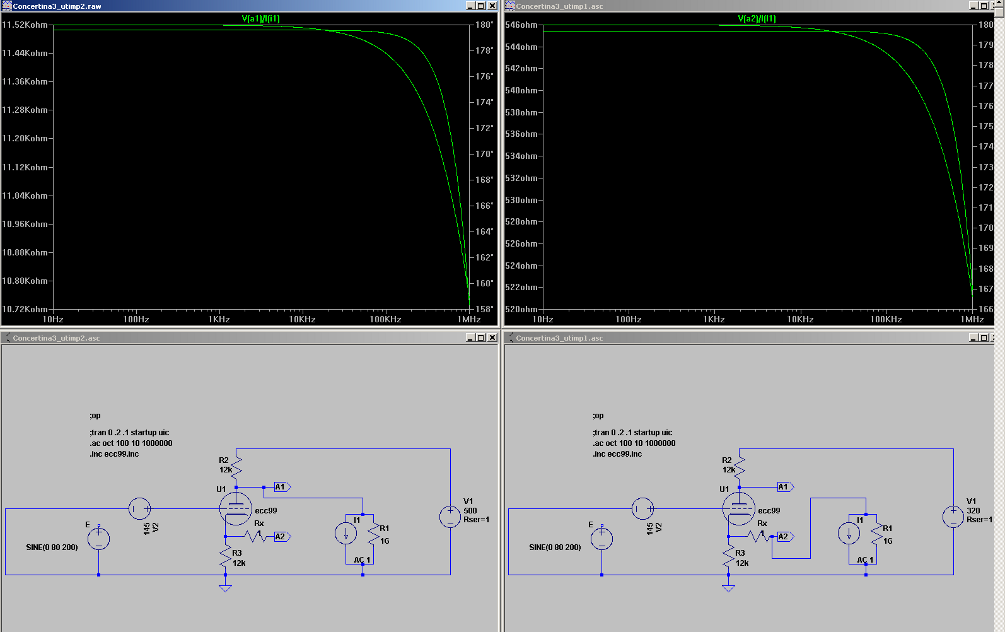
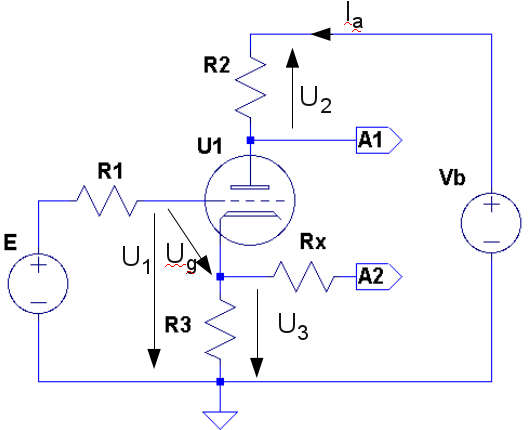
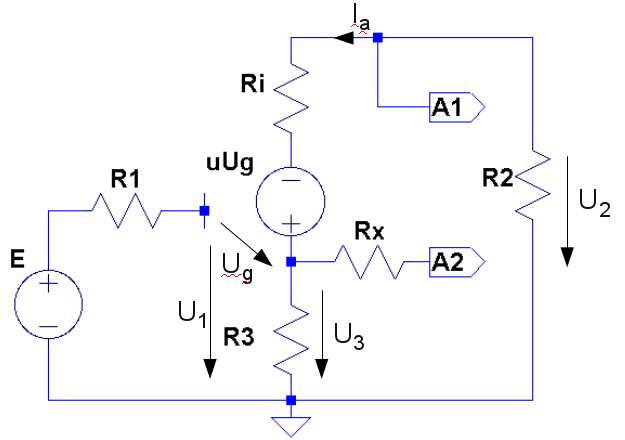
 |
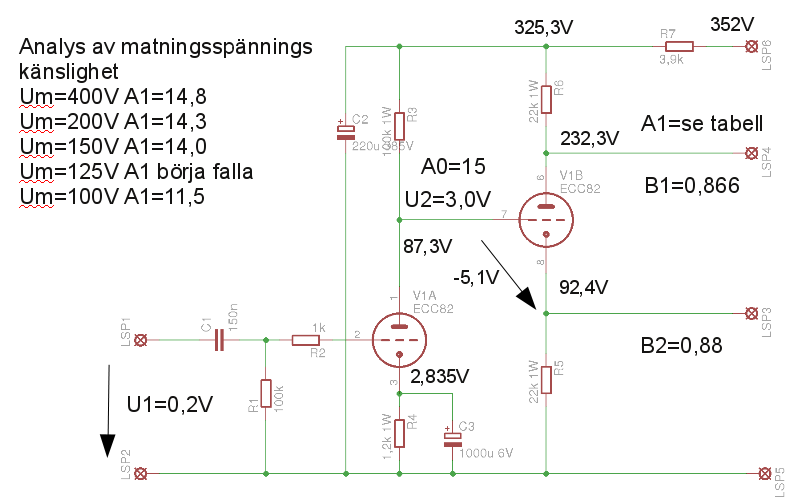
 |
Sökt:
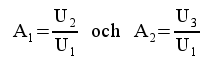 |
samt |
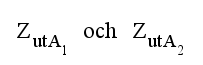 |
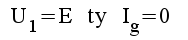 |
1.1 |
|
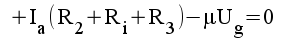 |
1.2 |
|
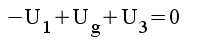 |
1.3 |
|
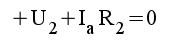 |
1.4 |
|
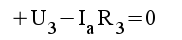 |
1.5 |
 |
 |
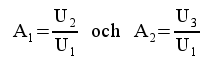 |
samt |
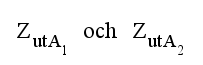 |
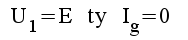 |
1.1 |
|
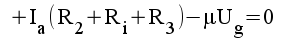 |
1.2 |
|
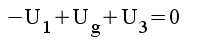 |
1.3 |
|
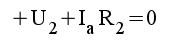 |
1.4 |
|
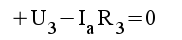 |
1.5 |
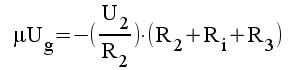 |
1.6 |
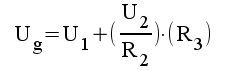 |
1.7 |
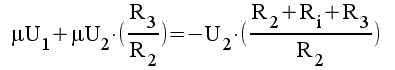 |
1.8 |
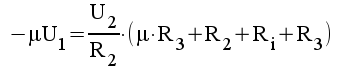 |
1.9 |
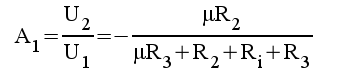 |
1.10 |
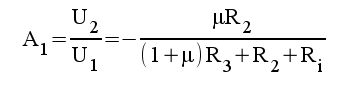 |
1.11 |
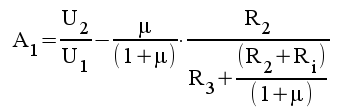 |
1.12 |
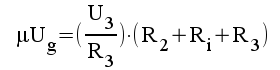 |
2.6 |
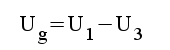 |
2.7 |
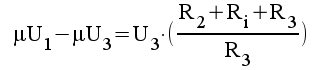 |
2.8 |
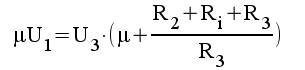 |
2.9 |
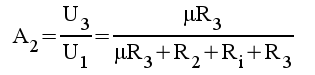 |
2.10 |
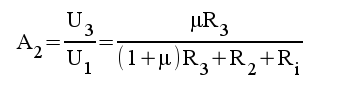 |
2.11 |
 |
2.12 |
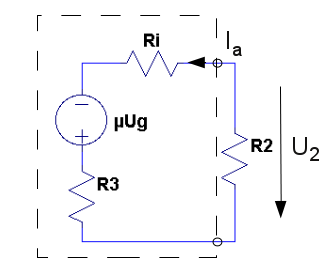
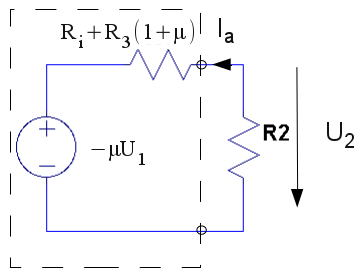
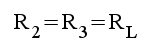 och skriver om 1.11 samt 2.11
på en vanligare förekommande form
och skriver om 1.11 samt 2.11
på en vanligare förekommande form 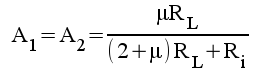
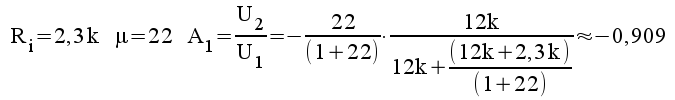
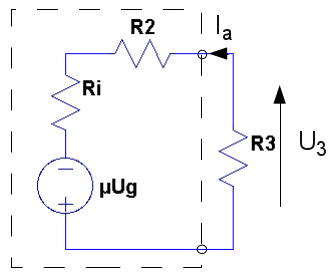
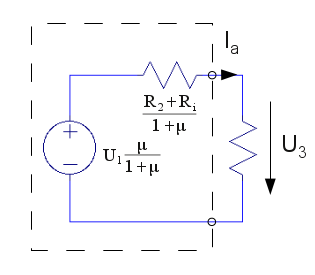
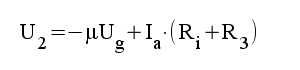 |
3.1 |
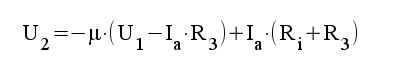 |
3.2 |
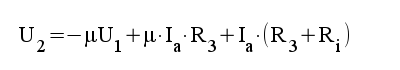 |
3.3 |
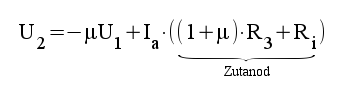 |
3.4 |
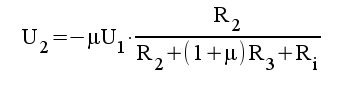 |
3.5 |
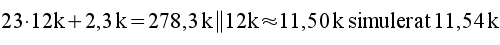 |
3.6 |
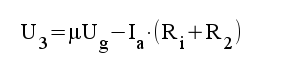 |
4.1 |
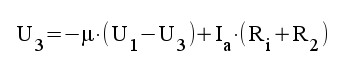 |
4.2 |
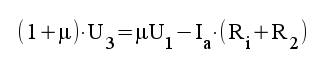 |
4.3 |
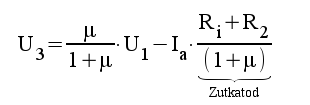 |
4.4 |
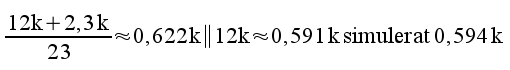 |
4.6 |
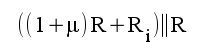 |
5.1 |
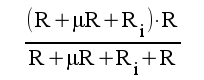 |
5.2 |
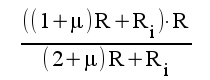 |
5.3 |
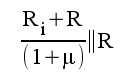 |
5.4 |
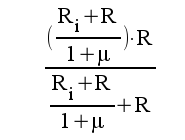 |
5.5 |
 |
5.6 |
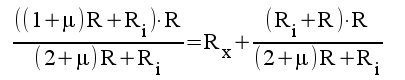 |
5.7 |
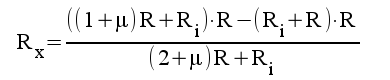 |
5.8 |
 |
5.9 |
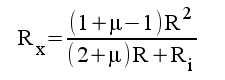 |
5.10 |
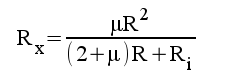 |
5.11 |
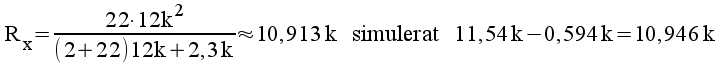 |
5.12 |