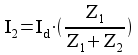Negativ resistans

Finns det något som heter negativ resistans? Jag skall i följande ge min syn på vad det i så fall skulle kunna vara. Men som vanligt är man aldrig först med något och när jag sökte på nätet, hittade jag en artikel i wiki som behandlar samma sak i samband med Colpitt-oscillatorer vilket även jag utgår ifrån.

Olinjära komponenter kan ha områden i sin karakteristik med negativ lutning ex. Tunneldiod, Tetrode och har därmed negativ resistans i detta område. Dock påstår jag att man med hjälp av aktiva element som inte har negativa områden i sin överföringsfunktion, kan skapa något som kan kallas för negativ resistans. Dessa kretslösningar utnyttjas ofta i oscillatorer vilket även jag ämnar göra med min lösning.

En oscillator kan konstrueras på flera olika sätt och en närmare analys finns i H-kompendiet under elektronrörsoscillatorer. Villkoret för stationär svängning tecknas

H1.1

som utgör villkoret för stationär svängning i systemet. H1.1 benämns ofta Barkhusens svängningsvillkor, i ord kan uttryckas på följande sätt:

för stationär svängning fordras att komplexa spänningsförstärkningen runt återkopplingsslingan (slingförstärkningen) är +1

Svängningsvillkoret kan även uttryckas med sambandet

H1.2

eller, eftersom och är komplexa storheter, med sambanden

(amplitiudbalansvillkoret) H1.3

(fasbalansvillkoret) H1.4

som utsäger, att förstärkarens inspänning via återkopplingsslingan skall återföras till färstärkaringången till såväl amplitud som fas.

I det följande kommer jag att utgå ifrån en traditionell Colpitt-oscillator (den sista är hämtad från wiki och förtydligad).

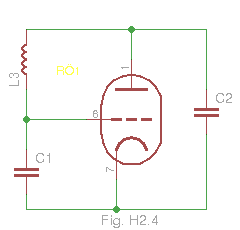
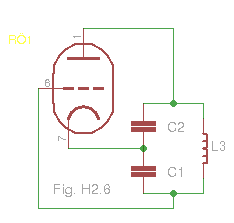
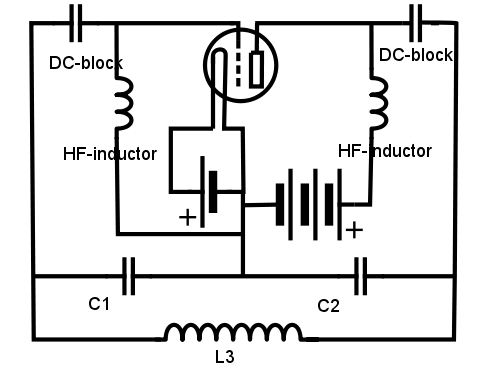
Likströmsmatning kan ske på olika sätt som jag inte kommer att gå igenom här. Det finns flera olika kompletta varianter att hitta på nätet.

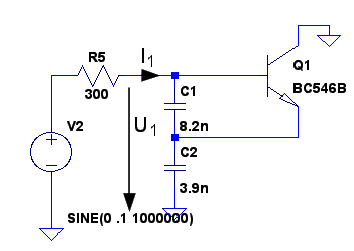
Nu utgår jag från en Colpittsoscillator där L3 tagits bort och vi betraktar inimpedansen mellan galler och jord. Vi tänker oss också att vi matar ingången med en växelspänning via ett motstånd. Min variant för LT-Spice finns här för nedladdning Negativ_resistans_modell (1 kB, updated 10 April 2009).

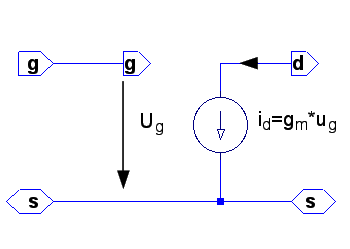
Förutsättningar: ett transistorsteg med en förenklad modell där vi bortser ifrån Rg samt Ri och betraktar endast h₂₁ som vi betecknar (transkonduktansen gånger Vbe som jag betecknar Ug istället för Vbe rör-gubbe som jag är vill ha gallerspänning eller gatespänning).

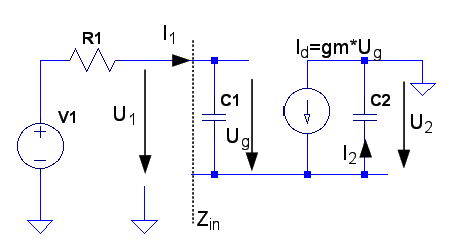
Jag får följande ekvationer:

=> Kirchoffs lag 2: summan av alla spänningar längs en sluten väg är noll

=> Kirchoffs lag 1: summa av alla strömmar till en knutpunkt är noll

=>

=>

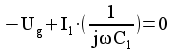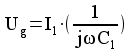
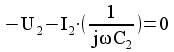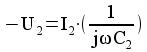
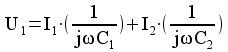
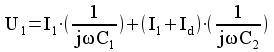
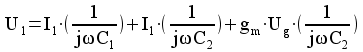
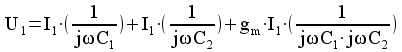
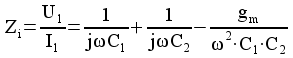
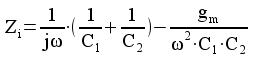
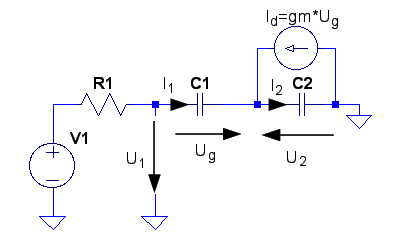
Resultatet kan alltså beskrivas med följande ekvivalenta schema:

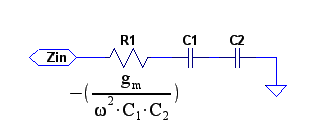
Tolkning av resultatet

Om man i serie med med ”ingången” kopplar in en induktans med samma reaktans som seriekopplingen av och kommer man att se en rent resistiv negativ reistans med värdet .
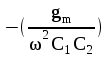Kopplar man i denna punkt in en serieresonanskrets med lägre förlustresistans, kommer man att få en oscillator.
Men vad betyder egentligen negativ resistans? Min tolkning är att spänning och ström är 180º ur fas och? att spänningen på andra sidan motståndet är större än påförd spänning.
Beräkning av növändig serieinduktans för 8,2nF i serie med 3,9nF vid 1MHz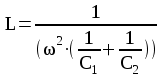
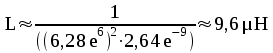
Labbkopplingar och mätningar

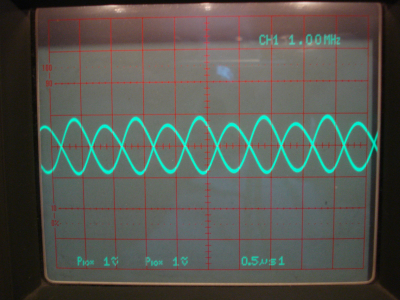
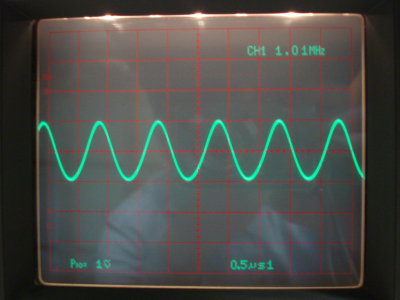
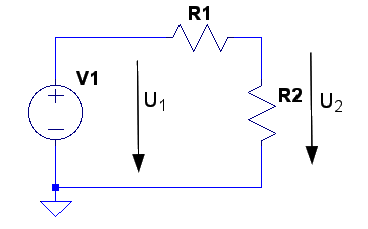
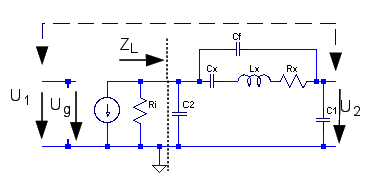
Om vi betraktar sista mätningen som en ren spänningsdelning får vi föjande schema för ingången

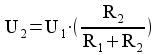
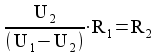
Uppmätta värden från labbkopplingen gav U1=246mV och U2=-21mV där R1=1000

Stämmer då detta med transistordata? Ja ganska bra ty det är svårt att skatta gm från diagrammet för BC546B

beräknat 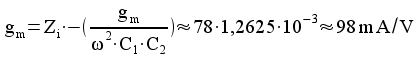från diagrammet ganska hyfsat för att vara skattade data. Man ser att både matningsspänning och var arbetspunkten ligger har stor påverkan på resultatet. Här kommer några andra uppskattningar som visar hur svårt det är att ur detta diagram ta ut gm

Hur välja C₁ och C₂? Ja det är inte resonansfrekvensen som bestämmer hur dessa skall väljas. Ju mindre de är, ju större är Zi och därmed den förlustresistans som kan kopplas in. Dock måste man också ta hänsyn till hur utstyrningen av transistorn blir. Väljer man 500pF + 500pF kan man också sänka matningsspänningen. Dock som man ser av det följande måste man också ta hänsyn till hur mycket ström man återkopplar till transistorn. I det följande visar jag hur det ser ut med en kristall (ekvivalent schema) istället för L3:

Här ser man att spänningen blir distorderad beroende på hur C₁ och C₂ väljs. Man kan naturligtvis beräkna basströmmen och här kommer ett förslag på hur detta kan göras:

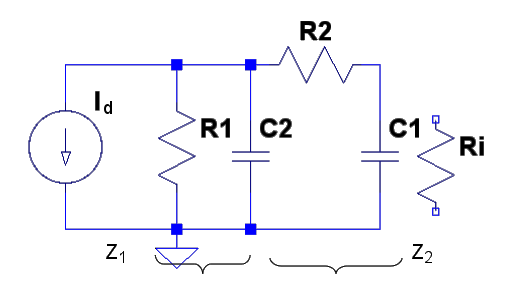
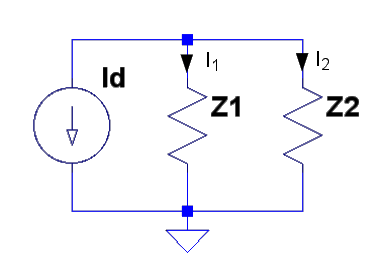
Om vi betraktar R₁//C₂ (h₂₂ och C₂) som Z₁ samt R₂ + C₁ eventuellt med basresistansen R_i kan man enkelt med strömdelning teckna strömmen I₂ genom Z₂: