< link link link >

    I en metall är atomerna fördelade på ett regelbundet sätt i ett kristalliniskt gitter. Kring atomkärnorna rör sig elektroner, varvid attraktionskraften på de inre närmast kärnan befintliga elektronerna är så stor, att de endast kan röra sig inom ett mycket litet område kring kärnan. Karakteristiskt för ledarna är, att de yttersta elektronerna på grund av det ringa atomavståndet i kristallen delvis påverkas även av kraftfältet från närbelägna kärnor. Dessa ytterelektroner är alltså så löst bundna till kärnan, att de kan sägas röra sig fritt i metallen. Dessa fria elektroner kan tänkas bilda en elektrongas, vars partiklar (elektroner) befinner sig i oordnad rörelse ungeför som partiklarna i en gas, med de kvarvarande atomresterna utgör fixa positiva laddningar t.ex. laddningen +e (om varje atom antages ha förlorat en elektron, som därmed är fri ; detta är approximativt fallet för koppar). Under inverkan av ett påtryckt elektriskt fält överlagras på denna oordnade rörelse en riktad rörelse hos elektronerna d.v.s. vi får en laddningstransport och vi säger, att en ström flyter genom ledaren.

    De fria elektronerna har vid absoluta nollpunkten alla möjliga hastigheter mellan noll och upp till ett största värde v_m. Hur antalet elektroner per volymenhet fördelar sig på de olika hastigheterna

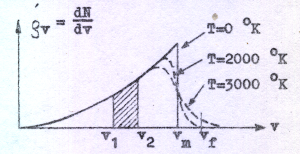		framgår av fördelningskurvan ( den s.k. Fermi-fördelningen) i fig. C1.1, där abskissan v är elektronhastigheten och ordinatan ρv är antalet elektroner per volymsenhet och hastighetsintervall. N är antalet elektroner per volymenhet i metallen.
Fig. C1.1

    Av fig. C1.1 ser vi, att


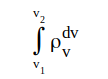anger hur många elektroner (per volymenhet), som har hastigheter mellan v₁ och v₂. Vidare är tydligen


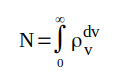    Av fig. C1.1 framgår även att fördelningskurvan defomeras, om metallens temperatur höjes. Det kommer då att finnas ett visst litet antal elektroner, som får hastigheter större än v_m (=maximalhastigheten vid absoluta nollpunkten).

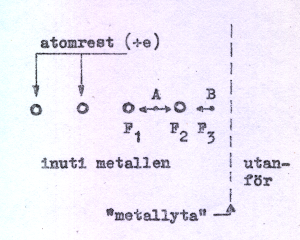
		Om nu redan vid absoluta nollpunkten vissa elektroner har avsevärd hastighet, varför rusar då dessa ej ut genom metallytan? Att så ej sker kan vi förstå med en smula eftertanke. Studera två elektroner i närheten av metallytan (se fig. C1.2, de betraktade elektronerna antages befinna sig i punkterna A och B). Om B-elektronen rör sig i riktning motmetallytan (vars läge vi av naturliga skäl har svårt att definiera)
Fig. C1.2

påverkas den hela tiden av en kvarhållande kraft F3 i motsats till A-elektronen. För att B-elektronen skomma loss fordras, att den övervinner attraktionskraften F3, d.v.s. den måste uträtta ett visst utträdesarbete. Elektronen måste alltså från början ha en viss minsta hastighet v_f (se fig. C1.1) för att kunna komma loss från metallytan (jämför: en kropp, som skall frigöras från jordens dragningskraft, måste utskjutas med en minsta hastighet av c:a 11 km/s). Hastigheten v_f är större än v_m, varav framgår, att en temperaturhöjning hos metallen (katoden) är nödvändig för elektronemission. Först då kommer, som synes av fig. C1.1, ett visst antal elektroner att få tillräcklig hastighet för övervinnande av metallytans attraktionskraft. Det bör påpekas, att hastighetskomponenten vinkelrätt mot metallytan måste vara större än v_f för att elektronemission skall äga rum. Vi ser av fig. C1.1 att högre katodtemperatur ger större antal frigjorda elektroner man observera å andra sidan vilken liten del av totalantalet fria elekroner i metallen, som verkligen emitteras.

    Betraktar vi nu det enklaste av elektronrören, tvåelektrodsröret eller dioden, som består av en evakuerad glasballong, innehållande två elektroder, den uppvärmda och elektronemitterande katoden och den elektronuppsamlande anoden, kan vi med ledning av vad ovan sagts formulera följande viktiga sats: katodtemperaturen bestämmer antalet för transport till anoden disponibla elektroner. Hur många av dessa, som verkligen nå anoden bestämmes däremot (som vi senare skall se) av spänningen mellan anod och katod. Antalet disponibla elektroner ger, om de alla går över till anoden den s.k. mättningsströmmen i_a0max, vars storlek kan teoretiskt beräknas (Dushmans emissionsformel):

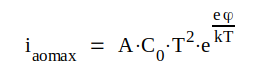C1.1

A = katodens area

C₀ = konstant innehållande universella konstanter

T = absoluta katodtemperaturen

e (i exponenten) = elektronladdningens belopp (1,60 · 10^-19 As)

k = Boltmanns konstant (1,38 ·10^-23 Ws/°K)

e·φ =utträdesarbetet, som är olika för olika katodmaterial.

φ  (volt) kan vi uppfatta som höjden av en i metallytan befintlig potentialbariär, vilken endast kan passeras av de fria elektroner som har tillräckligt hög Kinetisk energi.

     Logaritmerar vi ekvationen C1.1 erhålls


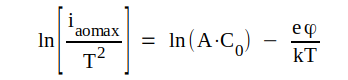     Sätter vi 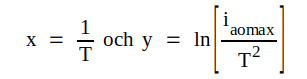 får vi


som är ekvationen för en rät linje i x-y-planet (se fig. C1.3)

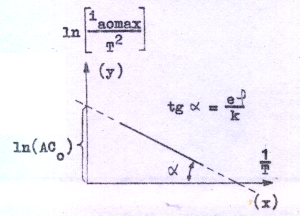		Genom att avsätta naturliga logaritmen för den uppmätta kvoten ia0max/T2 som funktion av 1/T kan vi alltså ur linjens lutning bestämma φ (utträdesarbetet). Ordinatan i origo ger med kännedom om A ett värde på konstanten C0.     Dylika mätningar ger för exempelvis volfram utträdesarbetet 4,52 eV och för barium 2,52 eV. På C0 får man för många metaller
Fig. C1.3

ett värde mindre än det teoretiska (120 A/cm²·K²). Avvikelsen har nöjaktigt kunnat förklaras.

    Stor mättningsström betyder enligt C1.1 att vi skall ha litet utträdesarbete (oxidkatod, torierad katod) och/eller hög temperatur (ren volframkatod).

link >