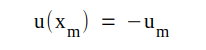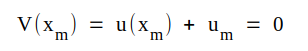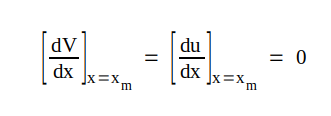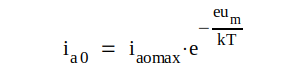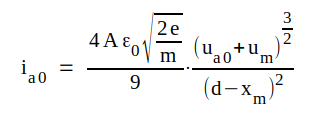Om dioden för enkelhets skull antages planparallell är, om katoden är kall, potentialfördelningen i röret linjär precis som i en plankondensator. Upphettas katoden kommer en negativ rymdladdning (=laddning per volymsenhet) att utbildas mellan katod och anod och denna rymdladdning bör vara störst i katodens närhet, eftersom de emitterade elektronerna där ej hunnit nämnvärt accelereras i anod-katodfältet. Närvaron av den negativa rymdladdningen sänker potentialen så att potentialfördelningen i röret ej längre blir linjär. Problemet att under dessa omständigheter beräkna strömmen genom röret försvåras av att olika elektroner starta från katoden med olika hastigheter (fig. C1.6).
Låt oss emellertid försöka oss på en beräkning under följande idealiserade antaganden:
- Dioden är planparallell och anod-katodavståndet är så litet jämfört med anodens och katodens diemensioner, att randeffekter kan försummas.
- Alla elektroner startar från katodytan med en och samma
utgångshastighet v0.
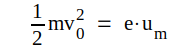 |
|
där e är elektronladdningens belopp och m elektronens massa. um (volt) benämner vi det mot hastigheten v0 svarande elektronvolttalet. Detta är alltså spänningen över det elektriska fält, som elektronen utan begynnelsehastighet måste genomlöpa för att erhålla den uppgivna hastigheten v0.
Utöver ovannämnda beteckningar v0 och um inför vi (se fig. C1.8):
- N(x) = antal elektroner/volymsenhet på avståndet x från katoden,
- v(x) = elektronhastigheten i planet x,
- u(x) = potentialen relativt katoden i planet x,
- D(x) = elektriska flödestätheten i planet x,
- K(x) = elektriska fältstyrkan i planet x,
- ia0 = anodlikströmmen
- ua0 = anodlikspänningen,
- A = katod- och anodarea samt
- d = katodavstånd.
 |
Låt oss
betrakta en ur rymdladdningen utskuren skiva med
tjockleken dx och arean A. Skivans volym är A·dx,
antalet elektroner i skivan är N(x)·A·dx och laddningen
i skivan är därför -e·N(x)·A·dx . Eftersom randeffekter
försummats blir det elektriska flöde, som netto går ut
från skivan A[D(x + dx) - D(x)] . Enligt ellärans flödessats (elektriska flödet genom en |
|
| Fig. C1.8 |
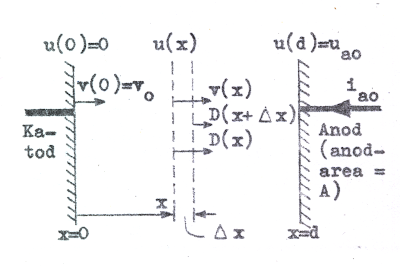
sluten uta är lika med den av ytan inneslutna laddingen) erhålles.
| |
som efter limesövergång
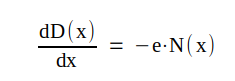 |
|
Vidare är
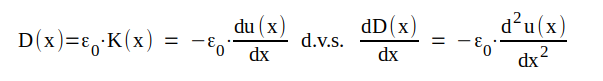 eller
eller 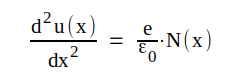 .
.Vi kan nu ställa upp följande fyra ekvationer
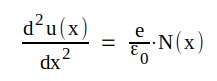 |
|
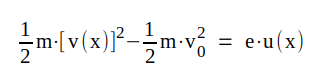 |
|
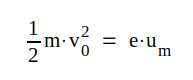 |
Elimineras v(x) och N(x) ur detta ekvationssystem får vi följande differentialekvation i u(x)
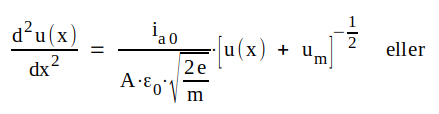 |
|
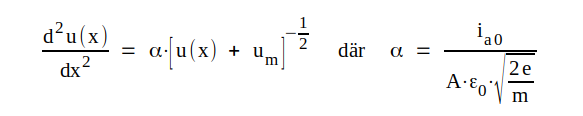 |
Differentialekvationen ovan blir något enklare om vi inför en ny funktion V(x) = u(x) + um. Vi får
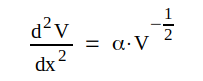 |
|
Vi multiplicerar med 2·dV/dx och får
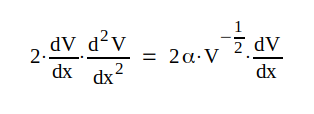 som kan
skrivas som kan
skrivas |
|
 |
Denna ekvation kan vi lätt integrera och därmed få reda på hur potentialen i röret varierar med x. Vid integrationen observerar vi problemets randvillkor. För något visst x-värde (som vi betecknar xm) måste potentialen i dioden sjunka till ett minimum -um d.v.s. u(xm) = - um.
Tänkt igenom varför. (Ledning: hur går det med strömmen ia0 genom dioden, om potentialminimumet är > respektive < -um ?). Potentialen i röret
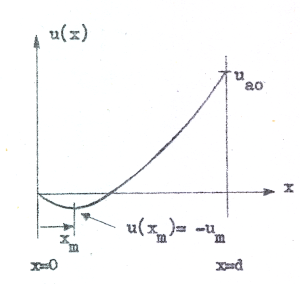 |
måste alltså variera ungefär
som i vidstående fig. C1.9. Vi integrerar därför lämpligen vår differentialekvation från x = xm till den godtyckliga koordinaten x. För x = xm gäller:
|
|||||||
| Fig. C1.9 |
Vi får alltså
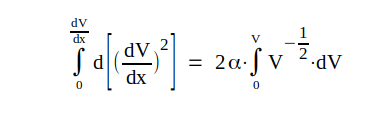 |
|
som ger
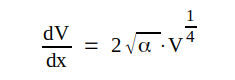 |
|
Ny integration mellan samma gränser ger
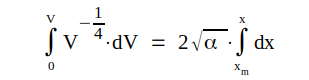 d.v.s.
d.v.s. |
|
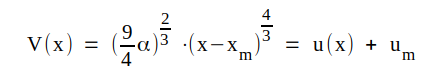 eller eller |
|
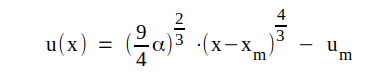 |
Vi har sålunda fätt ett uttryck på potentialfördelningen i röret. Tydligen måste nu det hittills obekanta xm ha ett sådant värde, att u(0) = 0, vilket leder till sambandet C1.6 nedan. Om vi slutligen i uttrycket på u(x) ovan sätter x = d så blir u(d) = ua0 och om vi inför uttrycket på α och löser ut ia0, så får vi sambandet C1.5 nedan d.v.s. ekvationen för diodens ia0-ua0-karaktäristik.
Med hjälp av den ovan skisserade beräkningsgången bör nu den mattematiskt intresserade läsaren lätt kunna verifiera riktigheten hos följande sammanfattande resultat.
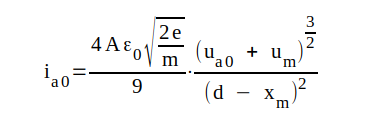 där där |
C1.5 |
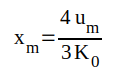 där där |
C1.6 |
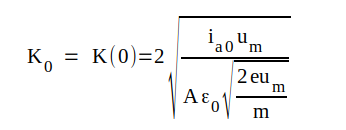 .
Vidare är .
Vidare är |
C1.7 |
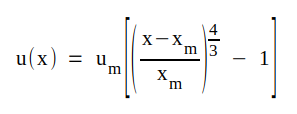 |
C1.8 |
 |
C1.9 |
 |
C1.10 |
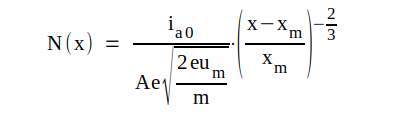 |
C1.11 |
Om elektronernas begynnelsehstighet försummas ( v0=0 d.v.s. um=0) blir xm = 0 och K0 = 0 och sambanden ovan får den enklare formen:
 |
C1.12 |
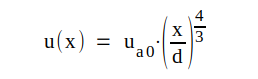 |
C1.13 |
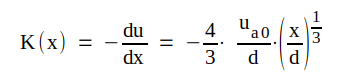 |
C1.14 |
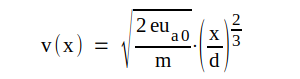 , ,
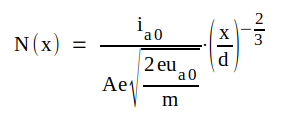 |
C1.15, C1.16 |
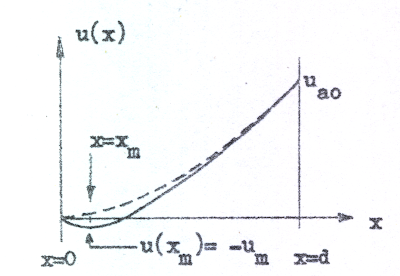
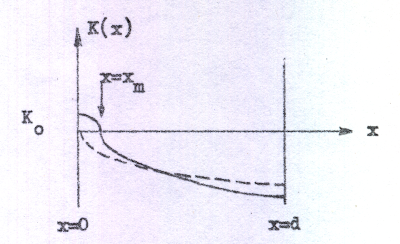
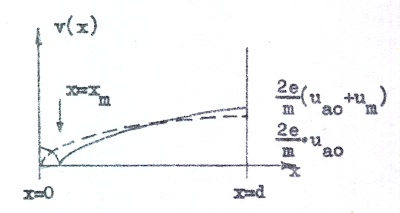
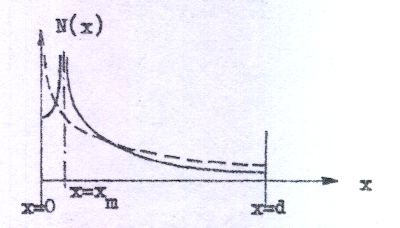
I kurvform får sambanden C1.8 - C1.11 följande allmänna utseende (heldragna kurvor). Som jämförelse (streckade kurvor) har i diagrammen inritats motsvarande kurvor, om elektronernas begynnelsehastighet vid katoden är noll (sambanden C1.13 - C1.16).
 |
 |
|
| Potentialfördelningen Fig. C1.10 |
Fältstyrkefördelningen Fig. C1.11 |
|
 |
 |
|
| Elektronhastigheten Fig. C1.12 |
Elektrontätheten (rymdladdningen) Fig. C1.13 |
Vi observerar alltså (fig. C1.10), att ett potentialminimum eller katodtröskel utbildas framför katoden och att vi där har en utpräglad rymdladdning (fig. C1.13). Av sambanden C1.6 och C1.7 framgår, att ju större anodströmmen är desto närmare katoden utbildas katodtröskeln.
Dock får vi ej glömma, att vi behandlat ett idealt fall, där samtliga elektroner antogs starta från katoden med en och samma begynnelsehastighet v0. Hur ställer det sig nu i praktiken, när elektronerna har olika begynnelsehastighet (fig. C1.6) ? Att ett potentialminimum utbildas även i detta fall bör väl vara klart och det är väl även rimligt antaga att potentialminimumet um får ett sådant värde, att de snabbaste elektronerna kan passera minimet medan de långsamaste återvänder till katoden. Betraktar vi fig. C1.10 bör vi kunna tänka oss vår praktiska diod som bestående av två seriekopplade dioder, en arbetande i begynnelseområdet och en arbetande i rymdlaggningsområdet (fig. C1.14). Strömmen i diod 1 bör därför bestämmas av sambandet C1.2, d.v.s. vi bör ha
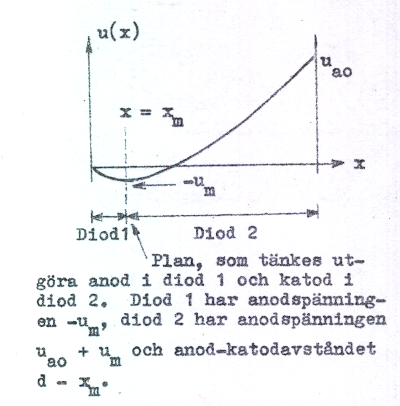 |
och eftersom potentialkurvan i diod 2 närmast övernsstämmer med den streckade kurvan i fig. C1.10 bör strömmen i diod 2 följa ekvation C1.12 med ua0 utbytt mot ua0 + um och d utbytt mot d - xm , d.v.s.
Även i praktiken bör vi sålunda få den redan härledda ekvationen C1.5 med den skillnaden, att um nu blir en funktion av anodströmmen. |
|||||
| Fig. C1.14 |
Löser vi nämligen ut um ur C1.17 ovan får vi
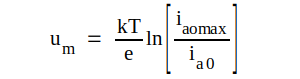 |
C1.18 |
varav framgår, att katodtröskelns höjd påverkas av anodströmmen. En temperaturhöjning hos katoden bör ha liten inverkan på anodströmmen, ty ökningen i katodens emissionsförmåga motverkas av tröskelns tillväxt. Går vi tillbaka till sambanden C1.6 och C1.7 ser vi att även katodtröskelns läge påverkas av anodströmmen, varför vi sammanfattar våra resultat i följande viktiga sats: Det är genom påverkan av katodtröskelns höjd och läge, som anoden genom sin spänning har förmåga att kontrollera anodströmmen.
Ökas anodspänningen kraftigt elimineras katodtröskeln och rymdladdningsområdet går kontinuerligt över i mättningsområdet. Detta antydes för övrigt av sambandet C1.18, som ger um = 0 när ia0 = ia0max.
Vad vi ovan sagt om den planparallella dioden gäller i princip även för dioder med godtycklig geometri.
Jämför vi slutligen vårt experimentella samband C1.3, som lyder
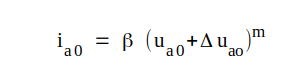 |
|
med vårt teoretiska uttryck C1.5, som lyder
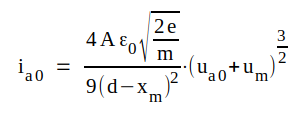 |
|
så finner vi, att
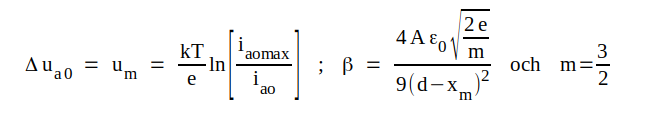 |
|
Sålunda är, som tidigare påpekats, för m = 3/2 varken Δua0 eller β verkliga konstanter, ty båda beror i någon mån av anodströmmen ia0.
link >