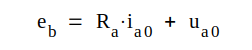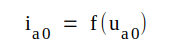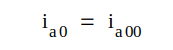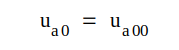< link link link >

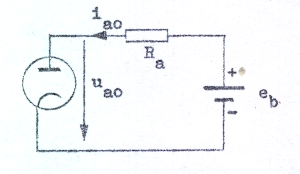
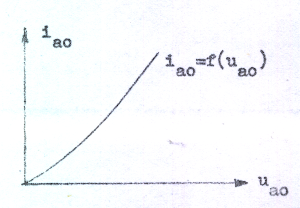
		Låt oss antaga, att en diod är uppkopplad enligt fig. C1.18. e_b och R_a förutsättes kända liksom diodens ia0-ua0-karakteristik, i_a0 = f(u_a0), given i form av en grafisk kurva enligt fig. C1.19. Problemet är att bestämma diodens anodlikström och anodlikspänning.
Fig. C1.18

Vi får två ekvationer, en ur Kirschoffs lag II och en är diodkurvans ekvation.

	C1.24
	C1.25

Vi har alltså en system av två ekvationer och vi har två obekanta

Fig. C1.19

i_a0 och u_a0. Ekvationssystemet kan alltså i princip lösas. Skillnaden gentemot ett normalt matematiskt ekvationssystem är, att en av ekvationerna är ett grafiskt samband.

Vi observerar, att C1.24 är ekvationen för en rät linje i i_a0-u_a0-planet. Denna linje, som benämner resistanslinjen för likström, är

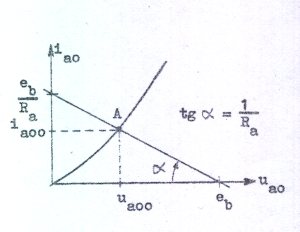inritad i fig. C1.20 (sätt i_a0 repektive u_a0 lika med noll, så erhålles lätt linjens skärning med koordinataxlarna). Eftersom lösningen till ekvationssystemet skall satisfiera såväl C1.24 com C1.25 måste de sökta ström- och spänningsvärdena återfinnas i skärningspunkten A i diagrammet.

Lösningen är alltså

	C1.26

Fig. C1.20

Punkten A benämer vi diodens vilopunkt och tillhörande ström- och spänningsvärden (i_a00 och u_a00) anodströmmens respektive anodspänningens vilovärde.

Anmärkning: I fig. C1.20 är resistanslinjens vinkelkoefficient -1/R_a och vi har därför något oegentligt satt tg α = 1/R_a , som har sorten ohm^-1 och som i detta sammanhang endast uttrycker, att förhållandet mellan "ordinatsidan" och "abskissidan" i den triangel, som bildas av resistanslinjen och koordinataxlarna, är 1/R_a. Detta är ett i många tillämpningar praktiskt skrivsätt. Observera dock, att alfa ej kan uppmätas med gradskiva. Olika skalor på axlarna ger ju olika vinkelvärden, medan hela tiden tg α = 1/R_a.

link >