< link link link >

    Vi studerar åter problemet i avsnitt 1.07. Vi drager en tangent till i_a0 - u_a0 - kurvan i vilopunkten A. Tydligen har vi då (se fig. C1.21)


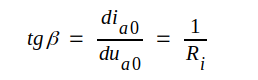    där vi infört beteckningen

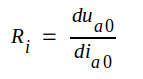C1.27

    R_i benämner vi diodens inre resistans mot anodspänningsändringar i vilopunkten A (eller blott inre resistansen [ibland förekommer benämningen växelströmsresistans eller dynamisk resistans] då risk för missförstånd ej föreligger). Diodens likströmsresistans i en godtycklig punkt (i_a0, u_a0) på karakteristiken är däremot

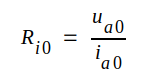C1.28

	Fig. C1.21

    Låt oss nu öka anodbatterispänningen e_b med Δ e_b. Anodströmmen och anodspänningen ökar då med Δ i_a0 och Δ u_a0 respektive d.v.s. vi hamnar i den nya punkten A' på karakteristiken. Efter ändringen gäller

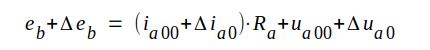C1.29

    Eftersom  erhålles ur C1.29
eller

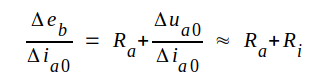under förutsättning, att ändringarna Δ i_a0 och Δ u_a0 är små.

    Alltså

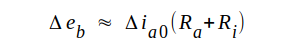	C1.30
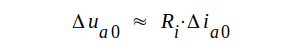	C1.31

    Detta system (C1.30 och C1.31) kan vi tolka som ekvationerna för kretsen i fig. C1.22 nedan.

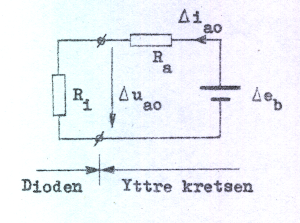		För små ström- och spänningsändringar kring vilopunkten verkar alltså dioden som en resistans med värdet Ri (beräknat i vilopunkten). Ändringar i ström och spänning kan alltså beräknas ur det enkla schemat i fig. C1.22. En dylik beräkning blir alltid approximativ, ty schemat innebär, att den krökta ia0-ua0-karakteristiken ersatts med en rät linje. För små ändringar får
Fig. C1.22

vi dock för praktiskt bruk tillfredställande noggranhet (något som från fall till fall får avgöras).

    Vi önskar nu utsträcka våra räkningar till att gälla små periodiska sinusformade ändringar, vilket är det viktiga praktiska fallet. Vi multiplicerar C1.30 ocnh C1.31 med cosomgat respektive j . sinomgat och adderar. Vi får (vi utbryter i fortsättningen ungefär mot = och ihågkommer att våra samband gäller små pendlingar kring vilovärdet.


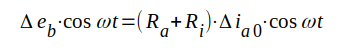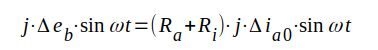Addition ger


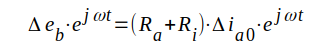    På analogt sätt erhålles


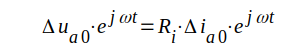    Tydligen betyder delta e_b, delta i_a0 och delta u_a0 vår växelkvantiteters amplitudvärden, varför vi infpr gängse beteckningar:


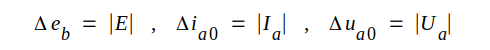    Slutligen inför vi komplexa strömmar och spänningar enligt nedan.


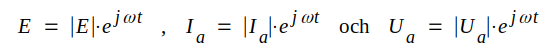    Vårt system C1.30-C1.31 övergår då till

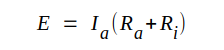	C1.32
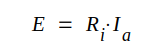	C1.33

    Vår räkning ovan innebär alltså, att vi gjort våra ändringar sinusformade i tiden samt att vi övergått till vår vanliga komplexa metod för behandling av växelströmsproblem. För de på vilovärdena överlagrade (små) växelkomponenterna gäller alltså C1.32 och C1.33, som vi kan tolka som ett ekvivalent växelströmsschema (småsignalschema) enligt fig. C1.23 nedan.

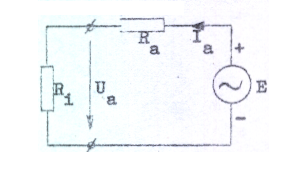		Småsignalschemat spelar kanke inte vid dioden så stor roll. eftersom dioden oftast arbetar med stora påtrycka växelamplituder. Vi har dock här ganska utförligt behandlat metodiken, ty vi skall senare finna, att dylika ekvivalenta schemor på analogt sätt kan härledas för övriga elektronrör och även för transistorer.
Fig. C1.23

    Vid radiofrekvens kan man ofta ej försumma inverkan av kapacitansen mellan anod och katod, varför i detta fall ekvivalenta schemat

		bör kompletteras med anod-katod-kapacitansen Cak, vilken i viss mån beror av rymdladdningen, något som lätt kan visas med utgångspunkt från räkningarna i avsnitt 1.03. Går vi slutligen till extremt höga frekvenser, kan schemat i fig. C1.24 ej sägas representera dioden på ett tillfredställande sätt. Här inverkar bland annat elektronernas ändliga gångtid mellan katod och anod. Detta är emellertid en fråga, som närmast hör mikrovågstekniken till.
Fig. C1.24

link >