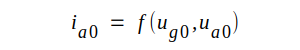< link link link >

    Om ett metalliskt galler (G) placeras mellan anod (A) och katod (K)

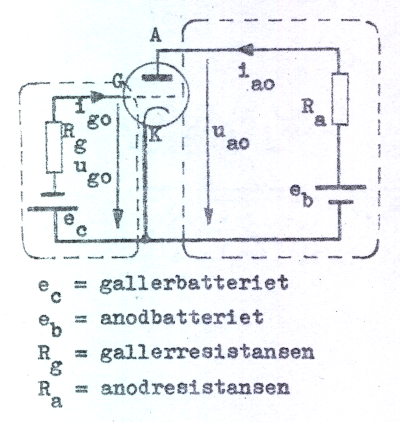		i en diod förvandlas denna till ett treelektrodrör eller triod. Vid elektronrören inför vi följande ström- och spänningskonventioner: en ström till en viss elektrod räknas positiv, då den går till elektroden, de olika elektrodernas potentialer anges i förhållande till katoden. Gallerkretsen respektive anodkretsen refererar till de båda streckade kretsloppen enligt fig. C2.1.     Vi förutsätter t.v. att gallerlikspänningen ug0 är negativ, vilket innebär, att gallerlikströmmen ig0 = 0 (med undantag av eventuell begynnelseström till gallret, då ug0 > c:a -1 Volt).
Fig. C2.1

		Eftersom gallerlikspänningen ug0 i likhet med anodlikspänningen ua0 måste påverka elektriska fältet i katodens närhet och därmed katodtröskeln, är det utan vidare klart, att anodlikströmmen ia0 måste vara en funktion av ug0 och ua0 d.v.s. C2.1
Fig. C2.2

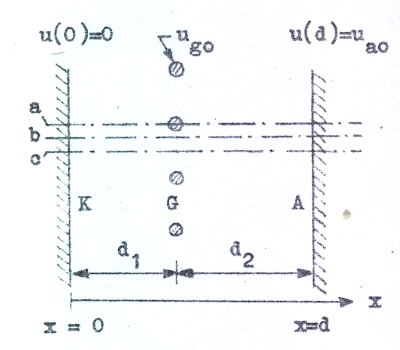
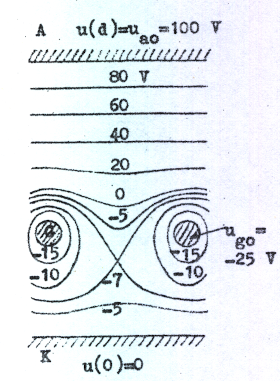
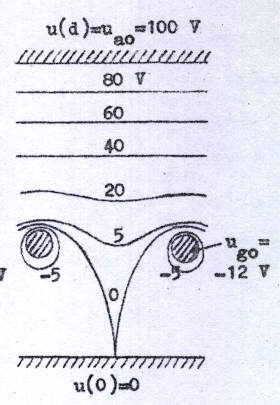
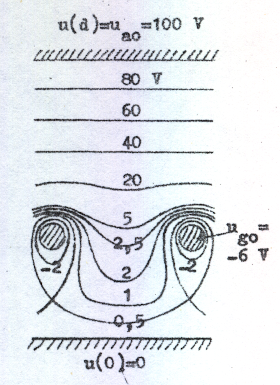
    Svårare att besvara är emellertid frågan, hur denna funktion ser ut. Det kan därvid vara instruktivt att som ledning studera potentialfördelningen i trioden. För enkelhets skull betraktar vi ett planparallellt system enligt fig. C2.2, där gallret antages bestå av ett antal inbördes förbundna ekvidistanta trådar, som alla ligger i ett plan parallellt med anod och katod. Till en början antager vi kall katod d.v.s. vi har ingen elektronemission, varför potentialfördelningen i röret är rent elektrostatiskt bestämd och kan beräknas. Resultatet av en dylik beräkning (eller uppmätning: kan Ni tänka Er någon metod för dylik uppmätning?) visas i fig. C2.3a, b och c, där ekvipotentiallinjer (ytor) uppritas för tre olika spänningskombinationer (Rita själv i diagrammen in de elektriska fältlinjerna).

Fig. C2.3a	Fig. C2.3b	Fig. C2.3c

    I fig. C2.3 observerar vi speciellt, att gallertrådarna ej åstadkommer en ekvipotentialyta i gallerplanet. Om de det gjorde skulle ju en elektron, som lämnade katoden, alltid stötas tillbaka för negativa gallerspänningar och vi skulle aldrig fån någon ström i ett sådant fall.

		Som av fig. C2.3b och c framgår är det på grund av den positiva anodens inverkan möjligt för en elektron att finna en väg från katod till anod utan att stöat på en potentialbarriär ("gallertröskel"). I fig. C2.3a däremot är gallertrådarnas potential så starkt negativ (-25 volt), att en potentialbarriär utbildas, röret är strypt.
Fig. C2.4

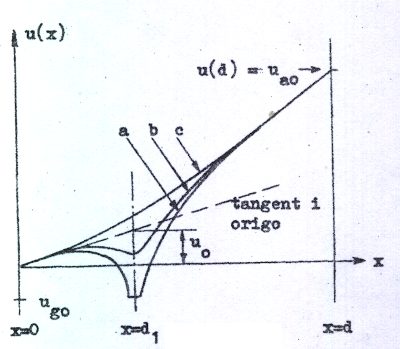
		Om vi nu i fig. C2.2 tänker oss att gallret är något negativt, skulle vi i de tre snitten a (=snitt genom och parallellt med gallertråden), b och c (snitt mellan gallertrådarna) få potentialfördelningen enligt fig. C2.4.     Observera, att samtliga tre potentialkurvor  har samma lutning vid katoden, vilket innebär, att elektriska fältstyrkan i katodens omedelbara närhet övarallt är densamma.
Fig. C2.5

Drager vi så till potentialkurvorna en tangent, som tangerar i origo, så skär denna tangent gallerplanet i en punkt, som har x = d₁ och u = u₀ (fig. C2.4). Om vi nu tänker oss, att gallret tages bort och ersätts med en plan elektrod på gallrets plats och med potentialen u₀ relativt katoden (fig. C2.5), så ändras ej elektriska fältstyrkan vid katoden. Vi har med andra ord fått en diod med anod-katod-avståndet d₁ och anodlikspänningen u₀. Följaktligen måste nu, om katoden upphettas (vi har ju hittills antagit kall katod), strömmen i_a0 i denna diod följa vår i avsnitt C1.03 härledda ekvationen C1.5 (sid. C1.10), d.v.s. vi får

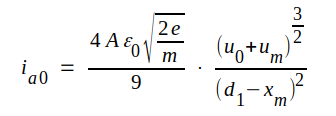C2.2

där	A	=	anod- och katoderna
	um	=	katodtröskelspänningen och
	xm	=	katodtröskelläget i enlighet med våra tidigare beteckningar.

     Eftersom gallret antagits negativt går ingen ström till detta (med undantag av eventuell begynnelseström, om u_g0 > -1 volt), varför sambandet C2.2 även uttrycker anodlikströmmen i vår triod. Vär ovan erhållna diod brukar därför benämnas triodens ekvivalenta diod.

    Kvar står emellertid att besvara frågan: hur beror den ekvivalenta diodanodspänningen u₀ av anodlikspänningen u_a0 och gallerlikspänningen u_g0? u₀ är direkt proportionell mot elektriska fältstyrkan vid katoden K₀=-u₀/d₁ och eftersom i ett elektrostatiskt fält fältstyrkan är en linjär funktion av elektrodpotentialen måste spänningen u₀ kunna skrivas exempelvis under formen

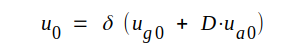C2.3

    där δ och D är "konstanter" ("-tecknen motiveras av att δ och D i någon mån beror av elektrodpotentialerna). δ brukar benämnas styrskärpan (0,5 - 1,0 för praktiska rör) och D, som är ett mått på anodens relativa effektivitet i gallerplanet, brukar benämnas anodens genomgrepp.

    Med C2.3 insatt i C2.2 får i_a0 formen

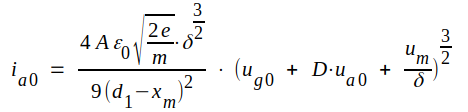C2.4

eller sammanfattat i likhet med diodens ekvation C1.3 (sif. C1.5):

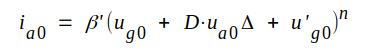C2.5

där vi infört beteckningarna


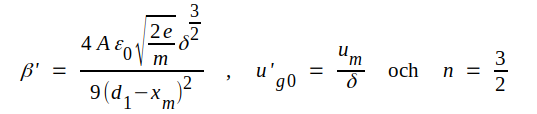    Därmed är tydligen det sökta funktionssambandet C2.1 bestämt (bortsett från det faktum att vi ej försökt oss på att beräkna värdet på det båda av för geometrin beroende "konstanterna" δ och D).

    Man brukar sätt u_g0 + D · u_a0 = u_sto, där u_sto benämnes triodens styrspänning. Korrektionen Δu'_g0 är normalt liten, varför vi med ledning av C2.5 ovan vågar påstå, att någon nämnvärd anodström ej flyter i trioden, såvida inte styrspänningen är positiv. Negativt u_sto skulle ju betyda negativ anodspänning på den ekvivalenta dioden d.v.s. ingen ström.

    Med n = 3 / 2 brukar C2.5 även vid trioden benämnas Childs lag eller "3/2-lagen".

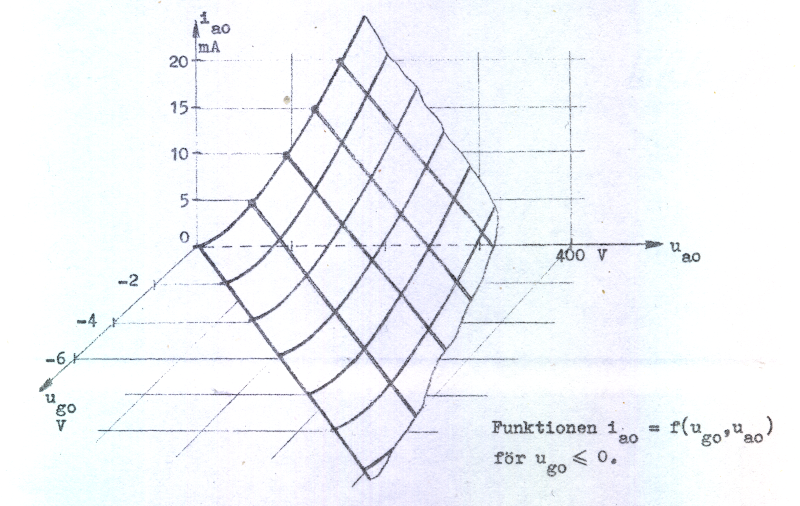
    C2.5 (en funktion av två variabler) kan tolkas som en yta, vars utseende, under förutsättning av konstanta värden på β', D, Δu_go och n, framgår av fig. C2.6 nedan.

	Fig. C2.6

    Fig. C2.6 är inget praktiskt sätt att ange en triods egenskaper. Vi har sett, att trioden (liksom övriga elektronrör) är ett icke-linjärt element. Det är därför svårt att beskriva i en enkel matematisk form. Childs lag kan sägas vara ett försök i den riktningen.

    Triodens och övriga rörs egenskaper framställes därför i diagramform i rörfabrikanternas datablad. Ekvationen C2.5 anger, som vi sett, en yta i i_a0-u_g0-u_a0-rummet men framställes normalt i nivådiagram. Beroende på valet av koordinataxlar benämner vi dessa diagram

                i_a0-u_a0-diagram (anoddiagram)
                i_a0-u_g0-diagram (överföringsdiagram) och
                u_g0-u_a0-diagram (konstant-ström-diagram).

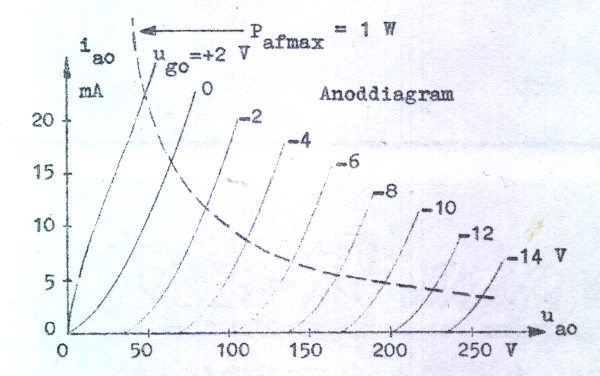
    Exempelvis erhåller vi en av i_a0-u_a0-diagramets kurvor ur fig. C2.6 som skärningslinjen (nivålinjen) mellan ytan och planet u_g0=konstant. I fig. C2.7 har vi i tur och ordning valt u_g0 = +2, 0, -2, -4, -6 .... volt och uppritat mostsvarande nivåkurvor, som tydligen, under förutsättning av konstanta β', D, Δu_go och n, är ett antal likadana utefter u_a0-axeln parallellförflyttade diodkurvor. De två övriga diagramtyperna erhålles på analogt sätt som skärningslinjerna mellan ytan och planet u_a0= konstant respektive planet i_a0=konstant. Känner man en av diagramtyperna kan alltid de övriga konstureras.

  I fig. C2.7 har, som nämnts, en kurva inritats för positiv gallerlikspänning (u_g0=+2 volt). Denna kurva har som synes annan form än de övriga. Vår teori ovan gäller även för positiva gallerspänningar, om vi låter i_a0 betyda katodströmmen. Då gallret är positivt kommer emellertid en del av katodströmmen att gå till gallret och en del till anoden, vilket är anledningen till kurvans avvikande form. Att beräkna strömfördelningen mellan galler och anod är ett besvärligt problem. Vi får anledning något beröra denna fråga i samband med flerelektrodrör.

		För trioder anges normalt anod- och överföringsdiagrammen. För sändartrioder anges ofta konstant-ström-diagrammet. I anoddiagrammet brukar kurvan för maximalt tillåten anodförlust (se avsnitt C1.06, sid. C1.18) inritas. Ekvationen för denna kurva är
Fig. C2.7

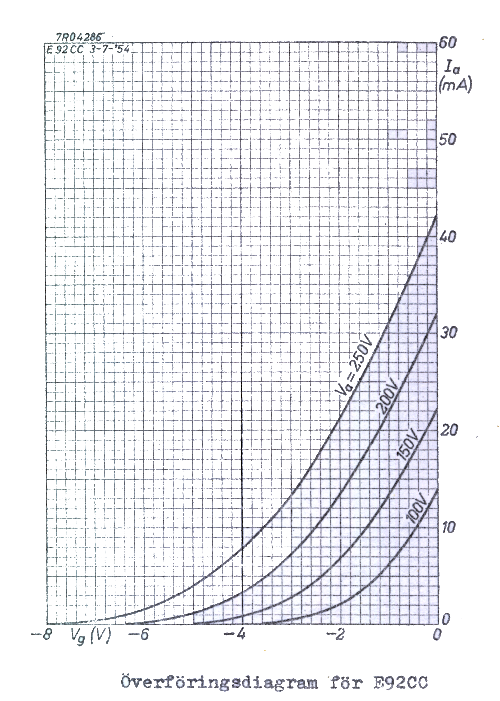
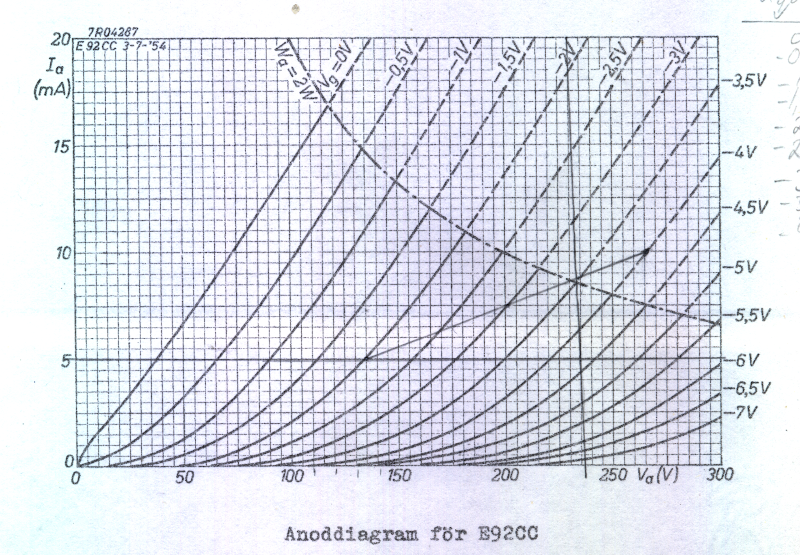
		Pafmax = ua0 · ia0 som tydligen är en hyperbel i anoddiagrammet (se fig. C2.7).     Principdiagrammet fig. C2.7 är idealt; kurvorna är parallella och ekvidistanta. För ett praktiskt rör beror våra konstanter β', D, Δugo och n i någon mån av elektrodpotentialerna, varför de praktiska rörkurvorna något avviker från de ideala. I fig. C2.8 och fig. C2.9 visas fabrikantens överförings- respektive anoddiagram för trioden (dubbeltrioden) E92CC (på axlarna användes fabrikantens beteckningar). Övning: Rita ug0-ua0-diagrammet för E92CC för ia0 = 5 resp. 10 mA.
Fig. C2.8

	Fig. C2.9

link >