< link link link >

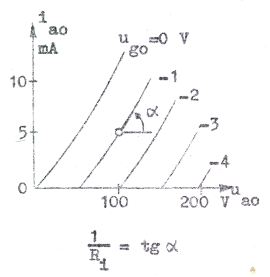
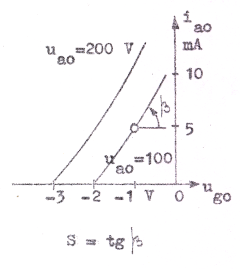
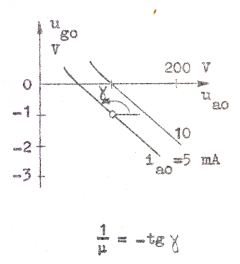
Den metodik, vi kommer att använda i fortsättningen vid räknemässig behandling av många kretsar, i vilka trioder ingår, kräver kännedom om lutningen på triodens karakteristiska kurvor (se fig. C2.15). Man har därför infört speciella symboler och namn, som hänger samman med kurvornas lutningsvinklar. Beträffande beteckningssättet nedan se anmärkningen på sid. C1.20 (kapitel 1.08).


Fig. C2.15a	Fig. C2.15b	Fig. C2.15c

Vi definierar triodens inre resistans mot anodspänningsändringar R_i (ibland benämnd växelströmsresistans eller dynamisk resistans) i en viss vilopunkt:

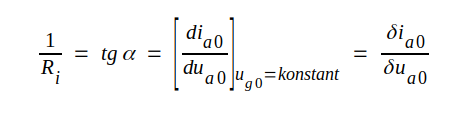Vi definierar triodens branthet S (även kallad transkonduktans eller ömsesidig konduktans ofta betecknad gm) i en viss vilopunkt:

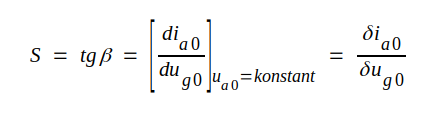Slutligen definierar vi triodens förstärkningsfaktor μ i en viss vilopunkt:

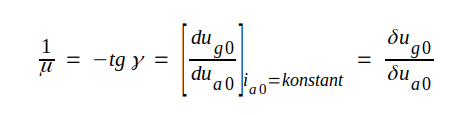Vi sammanfattar

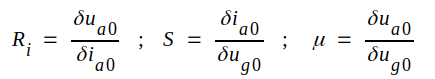C2.16

Triodens likströmsresistans i en godtycklig punkt (i_a0, u_a0) på karaktäristiken definieras liksom vid dioden av sambandet

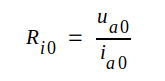C2.17

Betraktar vi ekvationen C2.5 (sid. C2.4) ser vi, att i_a0 = konstant betyder, att styrspänningen u_g0 + D · u_a0 = konstant. Deriverar vi detta samband med avseende på u_a0 erhålles

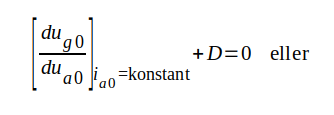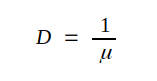C2.18

    För trioden är alltså genomgreppet inverterade värdet av förstärkningsfaktorn.

    Av skäl, som vi senare skall finna, benämnes R_i, S och μ lämpligen triodens småsignalparametrar. Andra benämningar är rörparametrar eller rörkonstanter, men småsignalparametrarna är inga verkliga konstanter, vilket en inspektion av en praktisk rörkurva genast visar. Vore samtliga rörkurvor räta linjer, skulle R_i, S och μ vara verkliga konstanter. μ håller sig tämligen konstant i praktiken, medan R_i och S varierar starkt inom vissa delar av diagramområdet. Det är därför viktigt vid angivande av småsignalparametrarna för ett rör att samtidigt omtala, vilken vilopunkt i rördiagrammet den karaktäristiska värdetrion R_i, S och μ avser.

    Småsignalparametrarna är ej oberoende av varandra utan två kända parametrar ger alltid den tredje, vilket vi lätt kan inse med utgångspunkt från vår enkla ursprungsekvation C2.1, som löd

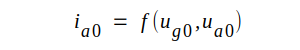Hålles i denna ekvation u_a0 = konstant medan u_g0 ändras med Δu_g0 fås anodströmsändringen genom enkel differentialräkning:

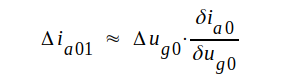Hålles i stället u_g0 = konstant medan u_a0 ändras med Δu_a0 blir anodstömsändringen på analogt sätt:

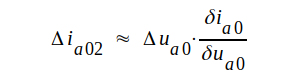Tänker vi oss sedan, att vi gjort båda ändringarna bör den totala ändringen i anodströmmen bli

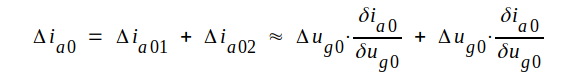Om slutligen ändringarna i Δu_go och Δu_a0 tänkes gjorda så, att Δi_a0 = 0, d.v.s. vi har hållit i_a0 = konstant får vi

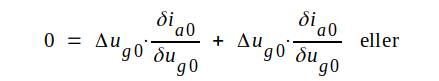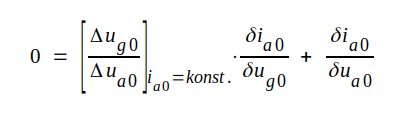som efter limesövergång ger

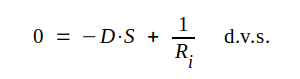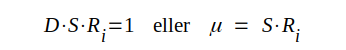C2.19, C2.20

    Låt oss så i tur och ordning något närmare beröra de olika småsignalparametrarnas beroende av vilopunkten.

    a) Brantheten S.

    Om 3/2-lagen antages gälla har vi enligt ekvation C2.5 (sid. C24):

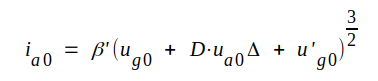Brantheten S blir alltså:

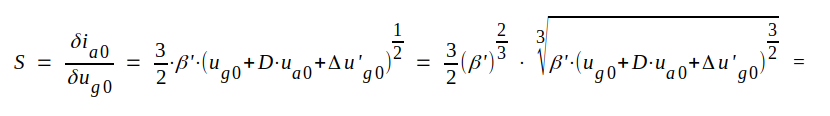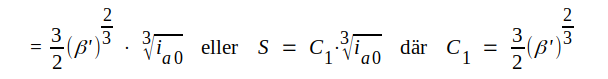C2.21

    För en triod kan vi alltså vänta oss, att brantheten är ungefärligen proportionell mot tredje roten ur anodlikströmmen.

    b) Inre resistansen R_i.

    På analogt sätt som under a ovankan man visa, att

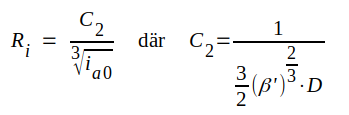C2.22

    För en triod kan vi alltså vänta oss, att inre reistansen är ungefärligen omvänt proportionell mot tredje roten ur anodlikströmmen.

    c) Förstärkningsfaktorn μ

    Eftersom μ = S · R_i får vi ur C2.21 och C2.22:

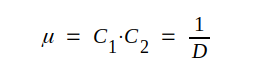C2.23

ett tidigare känt resultat (C2.18).

Om D är en konstant bör alltså μ göra skäl för namnet rörkonstant.

Låt oss något närmare söka utreda, varför μ som praktiken visar, är "den mest konstanta" rörparametern.

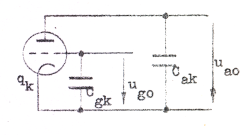
Hos ett kallt rör antager vi, att delkapacitanserna mellan galler och katod samt mellan anod och katod är C_gk respektive C_ak, d.v.s. vi har vidstående elektrostatiska schema för det kalla röret.
		Fig. C2.16

På katoden finnes en viss influensladdning q_k, bestämd av

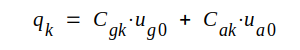Antag nu, att vi ändrar u_g0 med Δu_g0 och u_a0 med Δu_a0. Då kommer q_k att ändras med Δq_k och vi får

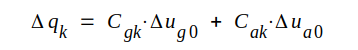Influensladdningen på katoden (q_k) och alltså även elektriska fältstyrkan framför katoden förblir trots spänningsändringarna konstant, om delta q_k = 0, d.v.s. om spänningsändringarna göres så, att

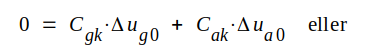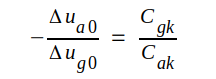Eftersom vi vet, att elektriska fältstyrkan vi katoden i ett varmt rör bestämmer katodströmmen (=anodströmmen i en triod med negativt galler) skulle tydligen anodströmmen bli oförändrad, om elektrodspänningarna ändrades på ovan beskrivet sätt. Vi skulle då kunna sätta

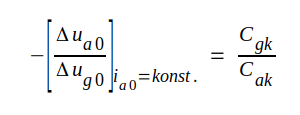Efter limesövergång är emellertid vänstra ledet ingenting annat än definitionen på förstärkningsfaktorn μ varför

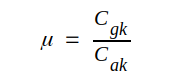C2.24

Enligt denna härledning är alltså μ en konstant, om C_gk och C_ak är konstanter. I ett varmt rör beror emellertid delkapacitanserna (i synnerhet C_gk) mer eller mindre av den rymdladdning, som finnes mellan elektroderna och vi får därför ej betrakta C2.24 som ett bevis för μ:s konstants. Sambandet bör dock ge en antydan om, varför μ, som praktiken visar, håller sig relativt konstant vid olika elektrodpotentialer.

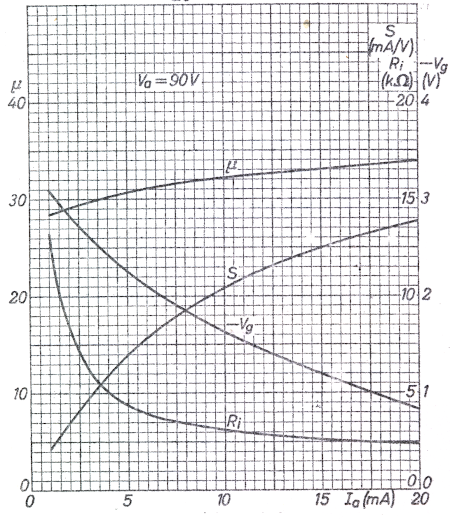
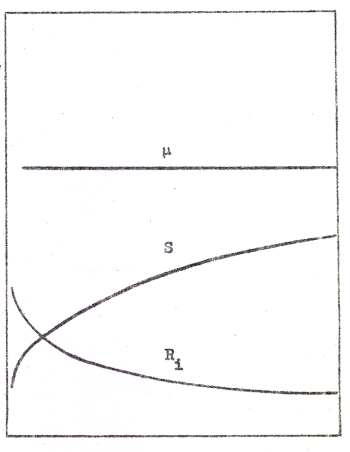
Under antagande av konstanta värden på 3/2-lagens β', D, Δu'_g0 och n, skulle våra teoretiska samband C2.21, C2.22 och C2.23 få utseendet enligt fig. C2.17. Som jämförelse visas i fig. C2.18 mostsvarande kurvor för ett praktiskt rör (E88CC; fabrikantens axelbeteckningar har bibehållits). Skalorna i de båda diagrammen är desamma och konstanterna C₁ och C₂ ovan har valts så, att det teoretiska röret har samma data för i_a0 = 8 mA.


Fig. C2.18		Fig. C2.17

link >