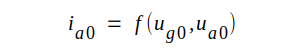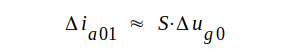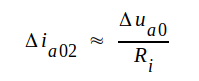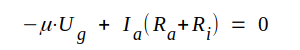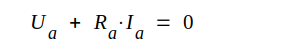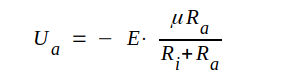< link link link >

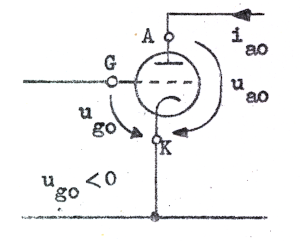
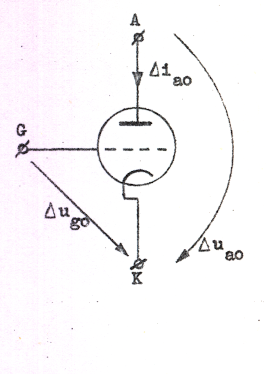
		För en triod enligt fig. C2.28 gäller, som vi tidigare sett, helt allmänt funktionssambanet C2.34     Låt os ge ug0 det lilla tillskottet Δug0 och ua0 det lilla tillskottet Δua0. Anodströmmen ia0 får då ett litet tillskott Δia0 och vi erhåller (jämför med räkningen på sid. C2.12 och C2.13):
Fig. C2.28

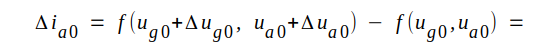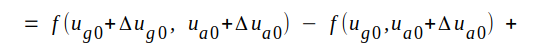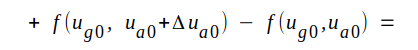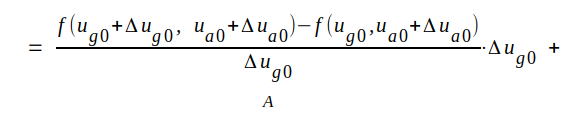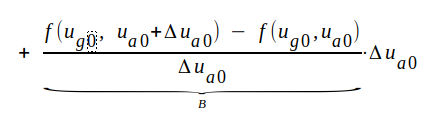    Om våra tillskott Δu_g0 och Δu_a0 är små, har vi

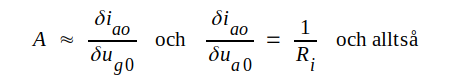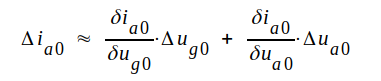C2.35

    Observera att vi ej åberopat någon speciell egenskap hos trioden. Sambandet C2.35 är därför en helt allmän egenskap hos en (kontinuerlig) funktion av två variabler och kan lätt utsträckas att gälla funktioner av flera variabler.

    Enligt våra definitioner i avsnitt C2.05 (sambanden C2.16, sid. C2.12) är


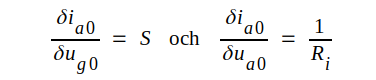varför vi ur C2.35 får:

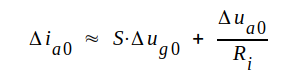C2.36

    Eftersom S · R_i = μ, kan C2.36 även skrivas på följande sätt

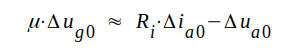C2.37

    Sambanden C2.36 och C2.37 ovan kan vi härleda på ett enklare sätt. Låt oss antaga, att vi i anoddiagrammet befinner oss i en vilopunkt (u_g00, u_a00, i_a00) enligt fig. C2.29 nedan.

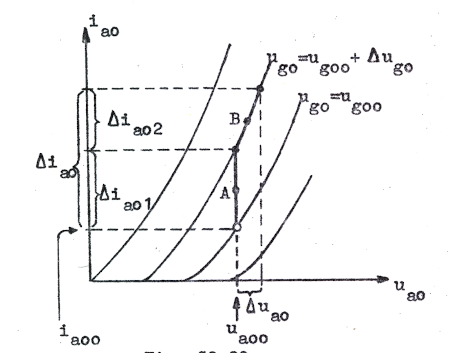		Ger vi först gallerspänningen tillskottet delta ug0 blir enligt definitionen på brantheten anodströmstillskottet där brantheten lämpligen bör beräknas i punkten A i diagrammet.     Ger vi sedan anodspänningen tillskottet delta ua0 blir enligt definitionen på inre resistans anodströmstillskottet
Fig. C2.29

där inre resistansen lämpligen bör beräknas i punkten B i diagrammet.

    Totala tillskottet i anodström blir alltså


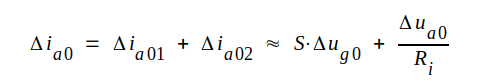    Skall detta uttryck, som överensstämmer med sambandet C2.36 ovan, gälla vid ändringar i godtyckliga riktningar kring vilopunkten inses, att vi med S och R_i nu lämpligen bör mena värdena i vilopunkten.

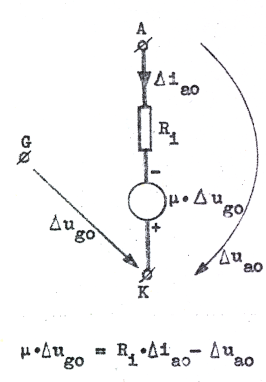
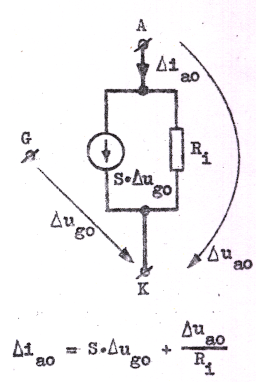
    För beräkning av små ström- och spänningsändringar från en viss vilopunkt räknat kan vi alltså använda de enkla sambanden C2.36 och C2.37, där μ, S och R_i är småsignalparametrarna, evaluerade i vilopunkten. Det för ingenjören speciellt viktiga i detta sammanhang är emellertid, att C2.36 och C2.37 kan tolkas som ekvationerna för det båda ekvivalenta småsignalschema, som visas i fig. C2.30 och C2.31 nedan.

Fig. C2.30	Fig. C2.31	Fig. C2.32

    I fig. C2.30 är röret beskrivet som en spänningskälla och i fig. C2.31 som en strömkälla. Det sistnämnda schemat kan givetvis erhållas ur det förstnämnda med hjälp av reduktionsreglerna i avsnitt A4 (sid. A4.1).

    Man kan inte nog understryka vikten av, att riktningarna på strömmar och spänningar måste definieras enligt figurerna ovan, om grundekvationerna C2.36 och C2.37 skall gälla.

T.ex. skulle en omkastning av riktningen på spänningspilen Δu_g0 (utan samtidigt teckenbyte på generatorn) i fig. C2.30 innebära, att schemat beskreve ett rör med följande egenskap (eller snarare egenhet): anodströmmen ökar, då gallret göres mera negativt!

    Eftersom vi räknar med konstanta värden (vilopunktens värden) på μ, S och R_i i våra ekvivalenta schemor, har vi i själva verket ersatt samtliga rörkurvor med räta linjer. Detta kan i fråga om procentuellt stora ström- och spänningsändringar var en grov approximation.

    I fortsättningen kommer vi vid användandet av sambanden C2.36 och C2.37 att utbyta (≈) mot (=) och ihågkommer i stället, att dessa grundekvationer gäller vid procentuellt små ändringar kring vilovärdena.

    Vi önskar så utsträcka våra räkningar till att gälla små sinusformade ändringar, vilket är det viktiga praktiska fallet. Vi kan därvid genomföra en diskussion liknande den, vi redan fört i samband med dioden (se sid. C1.22). Det torde därför utan vidare vara klart, att sambanden C2.36 och C2.37 övergår i C2.38 och C2.39 nedan efter införandet av komplexa storhetsbeteckningar.

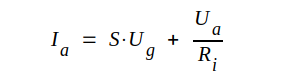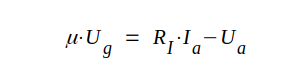C2.38 , C2.39

    I_a, U_a och U_g är alltså i komplex form de på vilovärdena överlagrade växelstorheterna. För fullständighetens skull ritar vi det mot C2.38 respektive C2.39 svarande ekvivalenta småsignalschemat (växelströmsschemat).

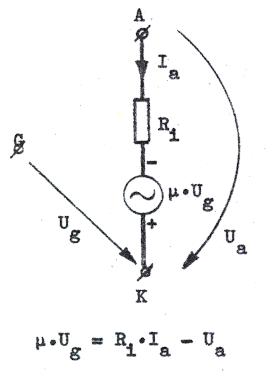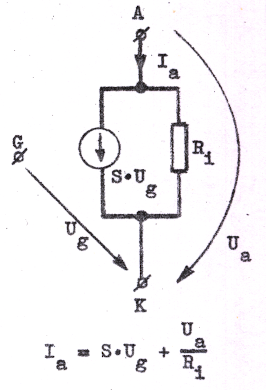Fig. C2.33	Fig. C2.34	Fig. C2.35

    Vid ett okritiskt betraktande av våra ekvivalenta scheman ovan kan dessa synas oberoende av vilopunktens data. Observera dock, att värdet på μ, S och R_i bestämmes av vilopunkten.

    Låt oss som ett enkelt exempel på småsignalschemats anvädning beräkna förstärkningen för den elementära spänningsförstärkaren enligt fig. C2.20 (sid. C2.17). Eftersom e_c- och e_b-batterierna ur växelströmssynpunkt är kortslutningar blir förstärkarens fullständiga ekvivalenta småsignalschema fig. C2.36 nedan.

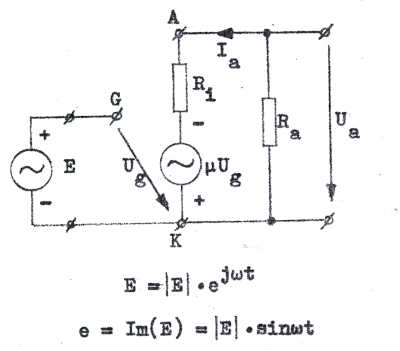		Kirchoffs lag II ger för galler och anodkrets följande ekvationer:     Eliminering av Ia och Ug ger
Fig. C2.36

    Videfinierar komplexa förstärkningen F som kvoten mellan komplexa utsignalspänningen och komplexa insignalspänningen.


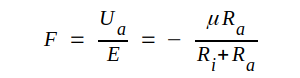    Förstärkningen (antalet gånger) blir


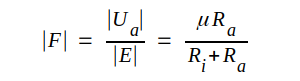ett resultat, som vi redan tidigare omnämnt (se C2.31, sid. C2.19).

    Av uttrycket på F ovan följer, att


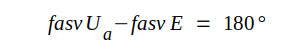    Vi kan även lätt beräkna utsignalspänningens momentanvärde, ty


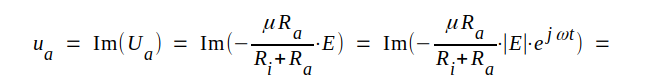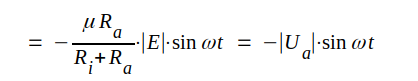    Med kännedom om anodvilospänningen u_a00 kan nu också få uttrycket på totala anodspänningen va:


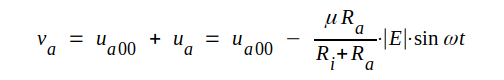    Samtliga resultat ovan står som synes helt i överensstämmelse med våra tidigare konstateranden i avsnitt C2.07 ovan.

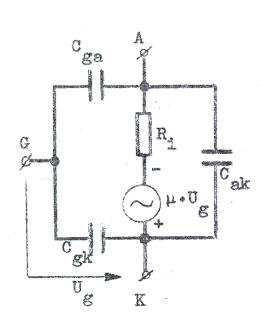
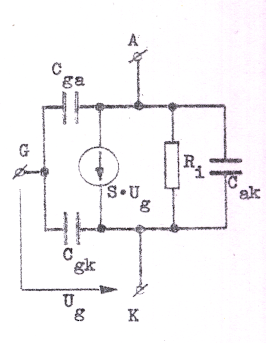
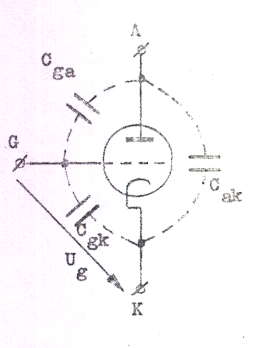
    Vid högre frekvenser kan schemorna fig. C2.33 och C2.34 ur signalsynpunkt ej sägas representera trioden på ett tillfredställande sätt, beroende i första hand på att kapacitanserna mellan rörets elektroder börjar spela en alltmer framträdande roll. Vi kan emellertid lätt komplettera ekvivalenta schemat genom att i detta införa rörets olika dlekapacitanser C_gk, C_ga och C_ak i enlighet med figurerna nedan. Vi får då ett växelströmsschema, som för små signaler tillfredställande representerar röret upp till relativt höga frekvenser. För en triod är C_gk och C_ga av storleksordningen någon eller några pF och C_ak är som regel något mindre. Speciellt C_gk är dock rymdladdningsberoende. I vissa fall kan även hänsyn behöva tagas till induktansen i elektrodtilledningarna. Vid extremt höga frekvernser, då bl.a. elektronernas ändliga löptid inverkar, år inget av våra schemor en tillfredställande beskrivning av rörets växelströmsegenskaper.

Fig. C2.37	Fig. C2.38	Fig. C2.39

link >