< link link link >

    Grafisk behandling av triodkretsar är relativt arbetsam och tidskrävande. I många fall, speciellt då kravet på noggrannhet ej är alltför stort eller då det gäller att principiellt bedöma en viss kopplings funktion, kan problembehandlingen avsevärt underlättas av lämpliga modeller, som eliminerar behovet av grafisk konstruktion. Det i avsnitt C2.09 behandlade ekvivalenta småsignalschemat är ett exempel på dylik metodik. I detta avsnitt skall vi emellertid närmast intressera oss för en approximativ modell giltig även för stora signaler.

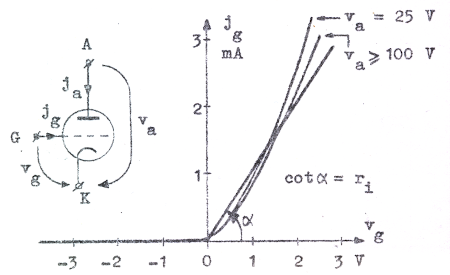		Är gallret hos en triod positivt drar gallret viss ström och galler-katod-sträckan fungerar i princip som en diod, vars data i någon mån beror av anodspänningen. Sambandet mellan gallerströmmen jg och gallerspänningen vg utgör triodens s.k. ingångsdiagram, var allmänna utseende för en typsik diod
Fig. C2.40

framgår av fig. C2.40. Låt oss approximera ingångsdiagrammet med en rät linje i första kvadranten jämte negativa v_g-axeln. Detta approximativa ingångsdiagram, som alltså utgöres av en av räta linjestycken sammansatt knäkurva, har samma form som diodkurvan fig. C1.26 (sid. C1.24). Galler-katod-sträckan kan därför approximativt beskrivas med en ideal diod i serie

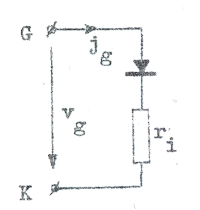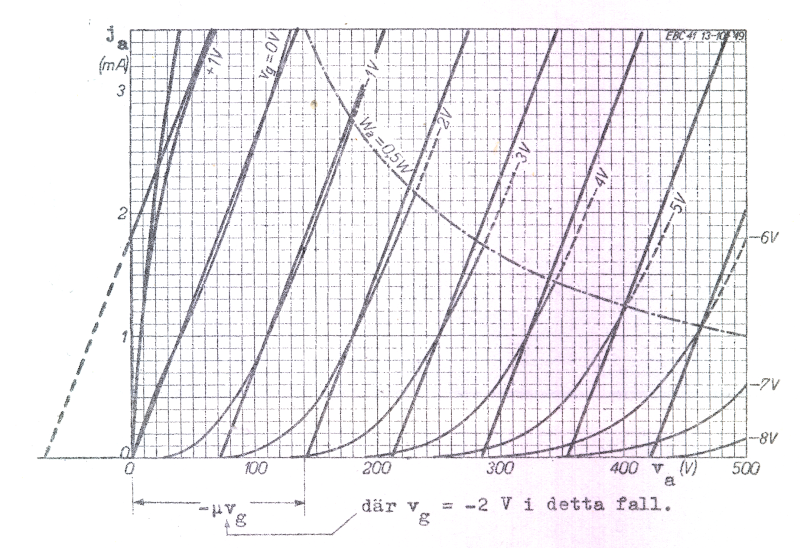
		med en viss resistans ri, vars värde hänger samman med linjelutningen i fig. C2.40. Se härtill fig. C2.41. Om vg < 0 spärrar dioden och jg = 0 som sig bör för negativa gallerspänningar.     Fig. C2.42 visar triodens anoddiagram. I detta ritar vi ett antal parallella och ekvidistanta linjer, som så nära som möjligt approximerar anoddiagrammets
Fig. C2.41

verkliga kurvor. För små anodspänningar och små anodströmmar blir som synes approximationen mindre god. Linjerna har sålunda alla samma lutning, vilket vi uttrycker med storheten R_i (R_i definieras alltså här som δv_a / δj_a för linjerna). I förhållande till linjen genom origo är övriga linjer förskjutna sträckan -μv_g, där μ är en konstant, vars värde av fig. C2.42 att döma nära överensstämmer med den förhållandevis konstanta rörparametern μ. Det ingen svårighet att inse, att skaran av räta linjer i anoddiagrammet berskrives av modellen i fig. C2.43, där dioden är ideal. Om v_a < -μv_g spärrar dioden, vilket överensstämmer med diagrammets krav. Om däremot v_a>-μv_g är den ideala dioden en kortslutning, d.v.s. vi har


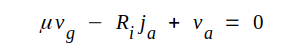som tydligen är ekvationen för diagrammets linjer.

	Fig. C2.42

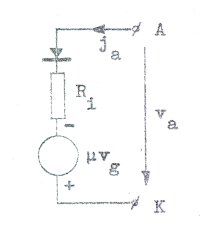		Av vårt resonemang följer, att trioden approximativt kan beskrivas med hjälp av en modell med schema enligt fig. C2.44. Vi har i vår diskussion använt beteckningarna v och j (jämför sid. C2.17) för spänning och ström för att betona schemats giltighet för såväl likstorheter som totala tidsvariabla storheter. Schemat har en inskränkning: schemat gäller ej för va < 0, om samtidigt vg > 0. Om t.ex. vg = +1 V innebär
Fig. C2.43

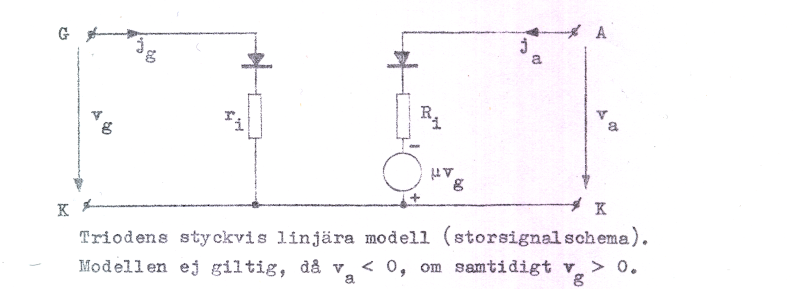
ett dylikt fall, att vi i fig. C2.42 hamnar på den streckade delen av kurvan för v_g = +1 V, vilket ej överensstämmer med triodens egenskaper.

	Fig. C2.44

   Efter inritning av diagrammets linjer bestämmer man lätt schemaparametrarna r_i, R_i och μ. Läsaren undersöker själv hur följande värdetrio erhållits ur fig. C2.40 och C2.42.


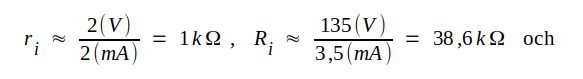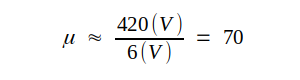    I detta sammanhang bör påpekas, att karaktäristikorna för ett visst rör kan avvika 10% eller eventuellt mera från de genomsnittskaraktäristikor, som rörfabrikanten publicerar för rörtypen i fråga. Med hänsyn härtill kan modellensanvändande i ett praktiskt beräkningsfall ofta ge fullt tillfredställande noggrannhet. De i diagrammen ritade linjekarakteristikorna har ett knä vid v_a-axeln respektive v_g-axeln. Dessa knän är de enda icke-linjäriteter, som modellen introducerar. I övrigt är modellen "linjäriserad" och den signalförvrängning (distorsion), som förorsakas av de praktiska rörkurvornas krökning, tar modellen ej hänsyn till.

link >