< link link link >

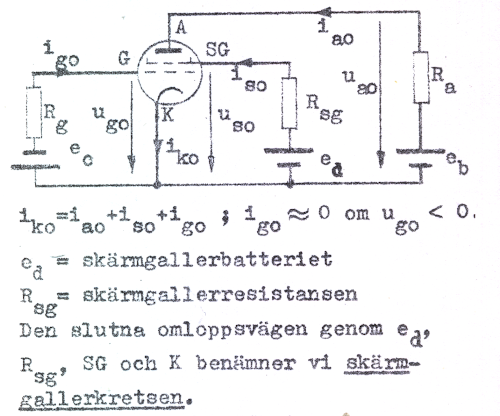
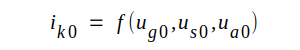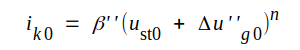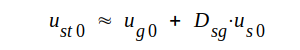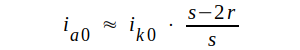      Om ett metalliskt galler (SG) insättes mellan galler (G) och anod (A) i en triod, erhålles ett fyrelektrodrör, en tetrod. Detta nya galler benämnes skrämgaller till skillnad från det ursprungliga triodgallret, som vi i fortsättningen benämner styrgaller (G i fig. C3.1 och C3.2). I motsats till styrgallret har skärmgallret i de flesta tillämpningar positiv förspänning (skärmgallerlikspänningen u_s0). I nedanstående fig. C3.2 över elektrodanordningen i tetroden har för enkelhets skull gallerstigningen s antagits lika för G och SG. a, b och c anger läget av tre plan, vars potentialsektioner framgår av fig. C3.3 (kall katod).

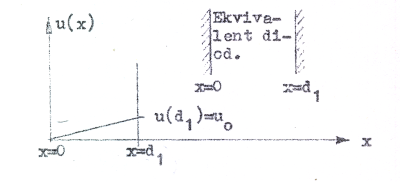
		Eftersom ug0, us0 och ua0 samtliga måste påverka elektriska fältet vid katoden och därmed katodtröskeln måste katodlikströmmen ik0 var en funktion av dessa tre spänningar d.v.s. C3.1     Då det gäller att beräkna ik0 kan vi, i likhet med behandlingen av trioden, tänka oss styrgallret ersatt med en massiv elektrod, som ges en sådan spänning,
Fig. C3.1

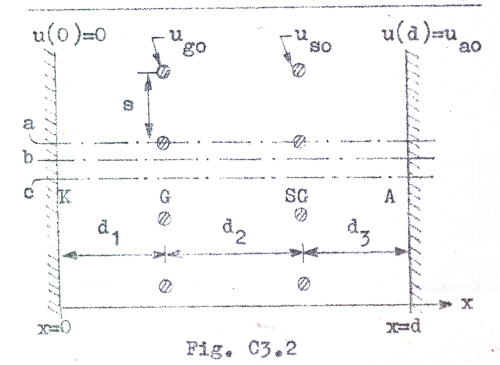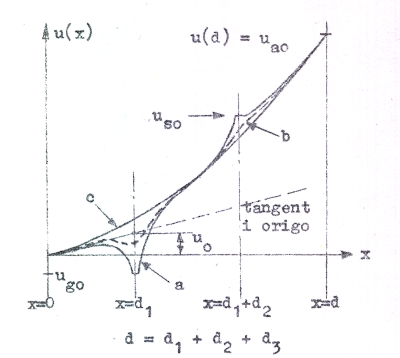
		att strömmen i den så erhållna dioden blir lika med tetrodens katodlikström ik0. Vi har då fått tetrodens ekvivalenta diod (se fig. C3.3 och C3.4). Den ekvivalenta diodanodspänningen u0 bör nu i analogi med triodfallet vara en linjär funktion av elektrodspänningarna och bör därför kunna skrivas
Fig. C3.2

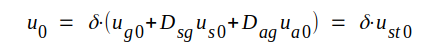C3.02

där δ , D_sg och D_ag är konstanter och där u_sto = u_g0 + D_sgu_a0 + D_agu_a0. Som tidigare i triodfallet benämner vi δ styrskärpan. D_sg och D_ag benämer vi skärmgallrets respektive anodens genomgrepp. u_sto kallar vi styrspänningen i styrgallerplanet.

		Man bör alltså i analogi med triodens ekvation C2.5 (sid. C2.4) kunna sätta C3.3 där β'' , Δu''g0 och n är "konstanter" i samma bemärkelse som motsvarande storheter i diod- och triodfallet.     Eftersom anoden är belägen så långt från katoden och dessutom effektivt avskärmad från denna genom två galler bör anodens inverkan på katodtröskeln vara ringa,
Fig. C3.3

		speciellt om skärmgallret är tätlindat. Med andra ord anodens genomgrepp Dag är mycket litet, vilket i sin tur innebär, att d.v.s. i huvudsak oberoende av ua0.
Fig. C3.4

    Detta betyder enligt ekvationen C3.3 att katodlikströmmen i_k0 vid konstant värde på u_s0 måste bli i det närmaste oberoende av anodlikspänningen u_a0. Däremot bör rimligtvis strömfördelningen (i_k0:s fördelning på SG och A) vid konstant u_s0 bestämmas u_a0.

    Låt oss något beröra strömfördelningsfrågan. Om u_a0 < u_s0 kommer skärmgallret att för elektronerna verka ungefär som en spridningslins verkar på infallande parallella ljusstrålar (beräkning av elektronbanor i dylika fall tillhör den s.k. elektronoptiken).

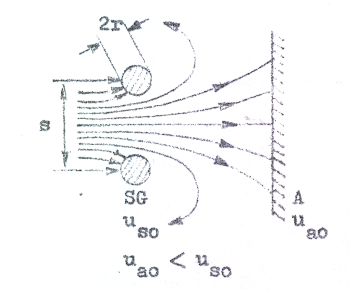		Vi nöjer oss här med att omtala, att man får elektronbanor ungefär som i fig. C3.5, d.v.s. en del elektroner kommer att återvända mot skärmgallret och upptagas av detta (eventuellt efter pendlingar kring skärgallerplanet). Med andra ord kommer ia0 att vara mindre än ik0. Ju lägre anodspänningen är desto större spridningsverkan får "skärmgallerlinsen" d.v.s. desto mindre blir ia0 jämfört med ik0.
Fig. C3.5

  Om u_a0 är avsevärt lägre än u_s0 kan man teoretiskt visa, att följande samband (Belows strömfördelningslag) gäller

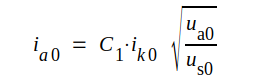C3.4

där C₁ är en huvudsakligen av rörgeometrin bestämd konstant.

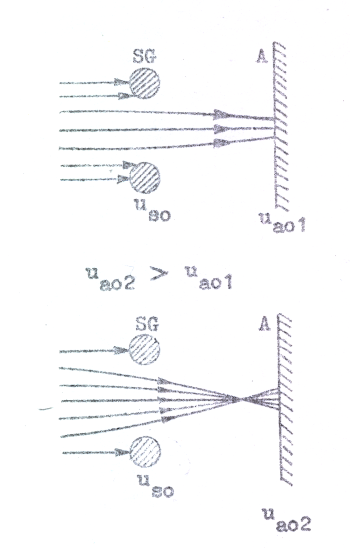		Om nu ua0 > us0 vänder inga elektroner mellan SG och A och till skärmgallret går nu i huvudsak så stor del av ik0, som bestämmes av den metalliska fyllfaktorn i skärmgallerplanet. Med beteckningar enligt fig. C3.5 bör alltså     En ändring av ua0 när ua0 > us0 inverkar med andra ord föga på ia0. Vi får dock ej glömma, att ua0 på grund av anodens genomgrepp i någon mån påverkar ik0. När ua0 > us0 verkar skärmgallret närmast som en samlingslins, vars brytkraft ökar med ökande ua0, varför vi enligt fig. C3.6 även av detta skäl kan vänta oss en ökning av ia0 med ökande ua0.
Fig. C3.6

Även för fallet ua0 > us0 kan man härleda ett teoretiskt uttryck på i_a0 (Tanks strömfördelningslag), som vi dock här förbigår.

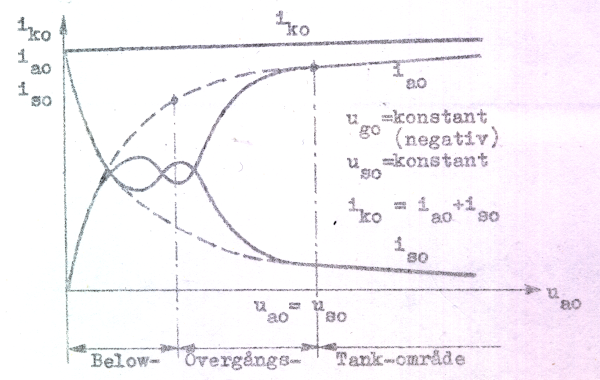
    Med ledning av vad ovan sagts bör i_k0 , i_a0 och i_a0 vid u_s0 = konstant bero av u_a0 på sätt, som framgår av fig. C3.7 nedan (streckade kurvor för i_a0 och i_s0).

		I praktiken visar sig karaktäristikorna följa de heldragna kurvorna i fig. C3.7. Vi har nämligen hittills bortsett från ett fenomen, som vid tetroden spelar en stor roll, sekundäremission. När primärelektroner från katoden med energier
Fig. C3.7

större än c:a 20 eV bombarderar anodplåten kan de ur denna slå ut sekundärelektroner. Om nu u_a0 < u_s0 attraheras dessa sekundärelektroner av skärmgallret, vilket innebär, att i_s0 ökar medan i_a0 minskar, ty summan av i_s0 och i_a0 är ju hela tiden ungefärligen konstant och lika med i_k0. När däremot u_a0 > u_s0 återvänder eventuellt utslagna sekundärelektroner till anoden och de streckade  och heldragna kurvorna i fig. C3.7 sammanfaller åter.

    Som redan nämts måste de infallande primärelektronerna ha en energi av minst c:a 20 eV för att man skall få någon nämnvärd sekundäremission. Detta är orsaken till att vi ej får någon svacka i kurvorna vid låga anodspänningsvärden. Huvuddelan av de frigjorda sekundärelektronerna har ganska låg energi, 2 - 10 eV. Sekundärelektronerna lämnar metallytan i godtyckliga riktingar. Antalet utslagna sekundärelektroner per infallande primärelektron, det s.k. utbytet, beror av flera faktorer. Sålunda ger snett infallande primärelektroner större utbyte än vinkelrätt mot ytan infallande. Utbytet är mindre för en ojämn yta än för en slät yta. Utbytet är lågt för de flesta rena metaller (<2 och ofta <1). För vissa specialbehandlade metallytor /t.ex. alkalioxidbeläggning) kan utbytet vara väsentligt större (5 - 10). Sekundäremissionen utnyttjas praktiskt i vissa specialrör (t.ex. elektronmulitplikatorer). Ett utbyte större än ett skulle för tetroden innebära, att anodströmmen skulle kasta om i_a0 - u_a0 - kurvan i fig. C3.7 skulle sålunda få svackans botten under u_a0 - axeln.

    Slutligen kan påpekas att sekundäremissionen kan uppträda även hos isolatorer. I vakuumrör för hög spänning kan det inträffa, att en liten fläck av glasbalongen på grund av primära ströelektroner uppladdas positivt, varigenom ytterligare elektroner attraheras. Om utbytet är större än ett blir alltså fläcken mer och mer positiv d.v.s. förloppet kan växa lavinartat, glaset mjuknar och en vakuumläcka uppstår. Botemedlet är ett tunt grafitlager (aquadag).

    När u_a0 > u_s0 kan sekundäremissionen i tetroden förorsaka en annan effekt än den ovan beskrivna, som ju inträffar, då u_a0 < u_s0. Om sekundärelektroner nämligen slås ut ur skärmgallret kommer ju dessa i detta fall att gå till anoden. Om utbytet är något större än ett kommer därvid skärmgallerströmmen att bli negativ och eftersom i_k0 = i_a0 + i_s0, kommer anodlikströmmen att bli större än katodlikströmmen.

    Svackan i tetrodens karaktäristik är av flera skäl icke önskvärd. Tetroden saknar därför numera i stort sett betydlese och tetroden är närmast att betrakta som en övergångstyp till pentoden, hos vilken svackan i karaktäristiken elimineras.

link >