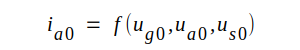< link link link >

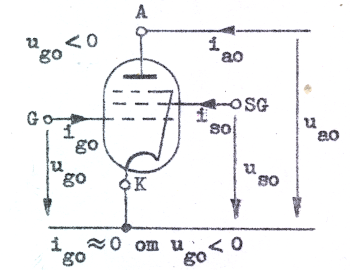
		För en pentod enligt fig. C3.21 gäller helt allmänt funktionssambandet C3.7     Om ug0, ua0 och us0 ges de små tillskotten Δug0, Δua0 och Δus0 får ia0 ett litet tillskott Δia0. Δia0 kan vi beräkna på samma sätt som i triodfallet (se sid. C2.22). Vi finner därvid att
Fig. C3.21

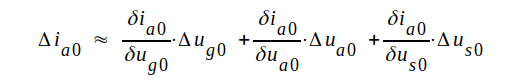C3.8

    Om vi nu gör det kompletterande antagandet, att skärmgallerspänningen u_s0 alltid hålles konstant, måste Δu_s0 = 0, d.v.s. sista termen i C3.8 försvinner. Efter införande av småsignalparametrarna S och R_i övergår därför sambandet C3.8 i sambandet

C3.9

vilket är exakt samma samband, som vi tidigare erhållit i triodfallet (se sambandet C2.26, sid. C2.23). Av vårt resultat ovan kan vi direkt draga följande viktiga slutsats: Om skärmgallerspänningen hålles konstant, gäller triodens ekvivalenta småsignalschemor även för pentoden (tetroden). Skillnaden mellan triodens och pentodens småsignalschemor består endast i att rörparametrarna har väsentligt olika värden för de båda fallen.

    Låt oss emellertid undersöka hur småsignalschemat modifieras, om skärmgallerspänningen tillåtes variera. Vi utgår åter från schemat fig. C3.21 och förutsätter som förut att u_g0 < 0 d.v.s. i_g0 = 0. vi förutsätter vidare följande allmänna funktionssamband:

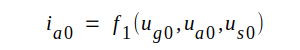C3.10

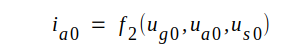C3.11

    Differentialräkning ger

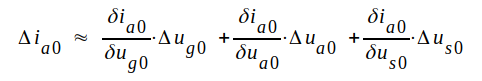C3.12

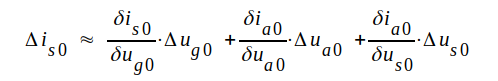C3.13

    Utöver parametrarn S och R_i måste vi nu tydligen definiera ytterligare fyra parametrar. Samtliga har diemension konduktans och vi inför därför beteckningarna


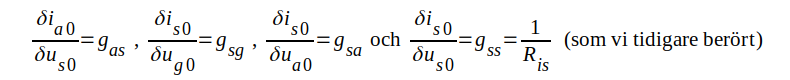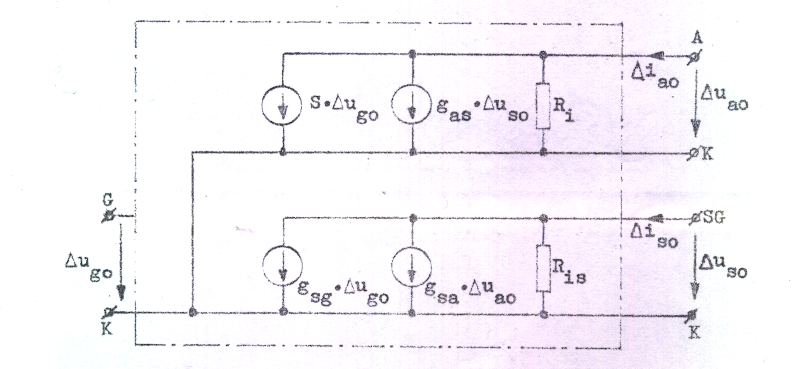
    Schemamässigt kan vi nu beskriva C3.12 och C3.13 med följande ekvivalenta småsignalschema

	Fig. C3.22

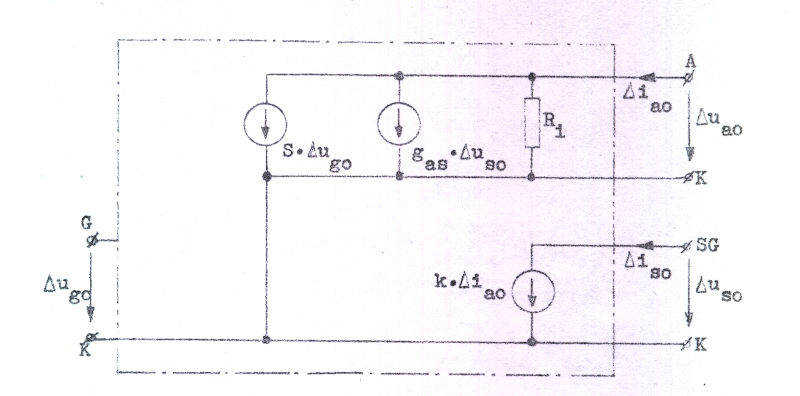
    Schemat fig. C3.22 kan något förenklas. I praktiken ligger pentodens vilopunkt normalt till höger om knäet i anoddiagrammet och här är i_s0 en tämligen konstant bråkdel av i_a0, varför vi kan sätta i_s0 = k · i_a0, där k är en konstant(Vilket approximativt värde på k erhålles exempelvis för EL84 ur diagrammet fig. C3.16, sid. C3.9). Av sambandet ovan följer att vi kan sätta Δi_s0 = k · Δi_a0 och schemat fig. C3.22 förenklas då till följande.

	Fig. C3.23

    Genom att införa "konstanten" k behöver vi nu endast en ny rörparameter, gas, som kan bestämmas exempelvis ur ett i_a0-u_a0-diagram. Givetvis kan parametern i fråga även bestämmas experimentellt.

    Observera slutligen att schemat fig. C3.23 övergår i triodens ekvivalentschema om Δu_s0 = 0, vilket vi ju förutsatte i vår första diskussion ovan.

    Schemorna ovan kan liksom i triodfallet kompletteras med rörkapacitanser och vidare kan vi givetvis övergå till komplexräkning.

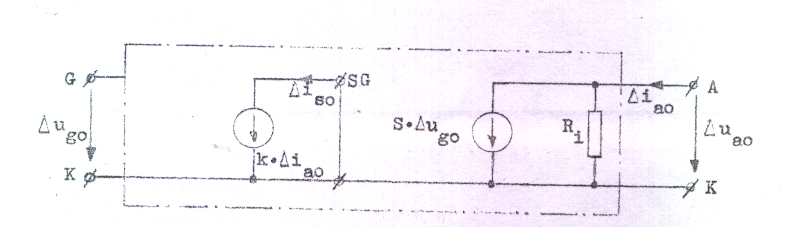
	Fig. C3.24

Pentodens ekvivalenta småsignalschema under förutsättning av konstant skärmgallerspänning (Δu_s0 = 0).

link >