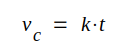< link link link >

    Skall elektronstrålen i ett katodstrålerör svepa över skärmen med konstant hastighet och därefter snabbt återgå till utgångsläget så fordras, att man mellan två samhörande avlänkningsplattor (vanligen x-plattorna) inkopplar en sågtandspänning (styckvis linjär svepspänning) enligt

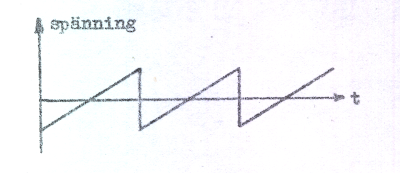		fig. C7.6. En tyratron kan med fördel användas i sågtandsgeneratorn (tidsaxelgenerator, svepgeneratorer).     Principen för alstring av en dylik spänning påminner om den enkla glimröroscillatorns (se sid. C5.11), men med en tyratron kan man på ett enkelt sätt
Fig. C7.6

få svepspänningen att exakt gå i takt med (synkront med) den signalspänning, som påföres katodstrålerörets andra plattpar (y-plattorna). Denna synkronisering är en förutsättning för att man på lysskärmen skall få en stillastående bild.

 Fig. C7.7 visar en principkoppling för åtstadkommande av såväl linjärt stigande svepspänning som synkronisering. Låt oss anta, att kapacitansen

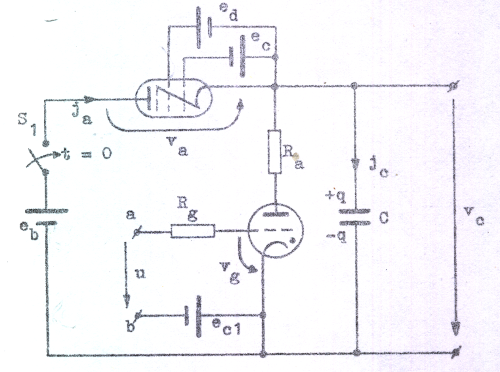		C från början är oladdad (q = 0), att (y-platt-) spänningen u = 0 (a och b förbundna) och att brytaren S1 slås till vid tiden t = 0. C börjar då laddas upp genom pentoden och vi önskar därvid, att kondensatorspänningen vc skall stiga linjärt, d.v.s. att där k = konstant.     Detta fordrar att kondensatorströmmen
Fig. C7.7

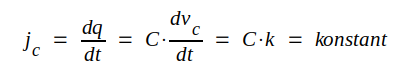C7.1

    En linjärt stigande spänning kräver alltså, att uppladdningen sker med konstant ström, något som vi just uppnår med hjälp av pentoden (eller något annat konstantströmselement). Hade uppladdningen skett via en resistans i stället för via en pentod skulle kondensatorspänningen stigit utefter en exponentialkurva (jämför fig. C5.15, sid. C5.11).

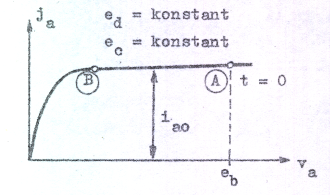		Vid t = 0 är vc = 0 och spänningen över pentoden är va = vs, d.v.s. vi befinner oss i punkten A på pentodkaraktäristiken (fig. C7.8). Allteftersom vc ökar under uppladdningen minskar spänningen över pentoden (va+vc=eb) och arbetspunkten för sig (med i huvudsak konstant ström ia0, fig. C7.8) från A mot B, vilket även gäller vc-tids-diagrammet
Fig. C7.8

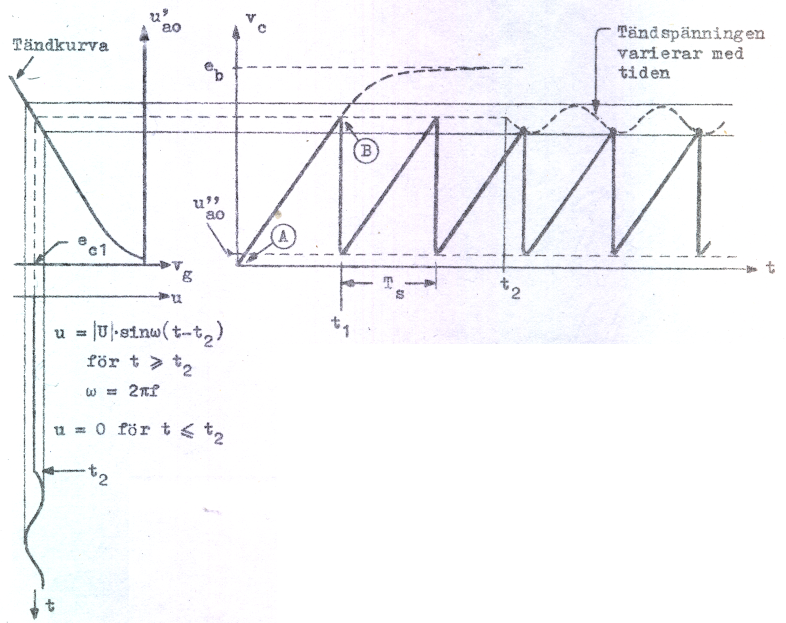
i fig. C7.9. Vid en viss tidpunkt t₁ är v_c = u'_ao = tyratronens tändspänning. C urladdas då snabbt (liten tidskonstant, skyddsresistansen R_s väljes så liten som möjligt) genom tyratronen, som slocknar vid släckspänningen u''_a0. Det linjära uppladdningsförloppet påbörjas nu åter, d.v.s. systemet självsvänger med en viss frekvens f_s = 1/T_s.

	Fig. C7.9

Låt oss nu vid tidpunkten t2 inkoppla den periodiska spänningen u, vars frekvens antages ungefärligen överensstämma med självsvängningsfrekvensen f_s, i serie med tyratronens vilogallerspänning (se fig. C7.7). Tyratronens tändspänning blir då en funktion av tiden på så sätt, som framgår av konstruktionen i fig. C7.9. Det är nu lätt att inse, att det i fig. C7.9 inritade fallet kan inträffa, nämligen att sågtandfrekvensen ställer in sig så, att den exakt övernsstämmer med signalfrekvensen f. Detta beror på att signalspänningen u nu bestämmer tändtidpunkten. Det inses även att ett flertal fall av dylik "låsning" mellan signal och sågtand kan förekomma, t.ex. så att sågtandfrekvensen blir exakt hälften av signalfrekvensen.

    I en praktisk svepgenerator av beskriven typ bör självsvängningsfrekvensen kunna varieras kontinuerligt, vilket kan ske genom reglering av laddningsströmmen (i_a0 i fig. C7.8). Detta åstadkommes enklast genom att reglera pentodens styrgallerförspänning. Stegvis frekvensändring kan ordnas genom inkoppling av olika stora kapacitanser C. För att få en smidig synkroniseringskontroll bör vidare tyratronens gallerlikspänning och signalspänningens amplitud kunna regleras.

    Om laddningsströmmen göres för stor kan anordningen sluta att självsvänga och man når ett stabilt tillstånd, där tyratronen brinner hela tiden d.v.s. pentodströmmen går genom tyratronen. För att undvika detta fall bör man göra laddningsströmmen mindre än den tyratronström, som erfordras för att bibehålla urladdningen i tyratronen.

    Slutligen bör påpekas att man med den beskrivna anordningen ej kan erhålla godtyckligt hög svepfrekvens, eftersom tyratronens tröghet kommer att göra sig märkbar vid hög frekvens. Metoden har emellertid stor principiell betydelse men har i ovan skisserad utförandeform närmast tillämpning i enkla oscillioskop med svepfrekvenser av storleksordningen tonfrekvens.

Övning: Undersök hur sågtandspänningen i fig. C7.9 förändras då, |U| göres allt större (översynkronisering).

link >