< link link link >

        Ett elektronrör, använt som förstärkare, kan i princip kopplas på tre olika sätt, nämligen med gemensam katod (GK-koppling), gemensamt galler (GG-koppling) och gemensam anod (GA-koppling) enligt fig.  F1.3, där vi för enkelhets skull antagit, att röret är en triod. Behandlingen nedan är dock tillämplig även för pentoder, om skärmgallret är katodförbundet ur signalsynpunkt.

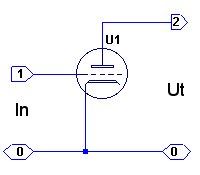GK-koppling.	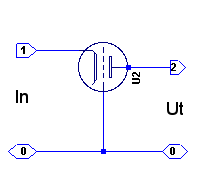GG-koppling.	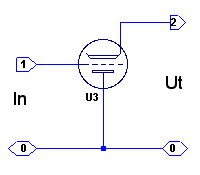GA-koppling.
Fig. F1.3. Elektronrörets tre grundkopplingar.

    Som introduktion till vårt förstärkarstudium kan det vara lämpligt, att vi bildar oss en allmän uppfattning om egenskaperna hos dessa olika kopplingssätt. Om vi förutsätter klass A drift och små signaler utgör elektronrörets ekvivalenta småsignalschema (se avsnitt C2.09 och avsnitt C3.05) ett lämpligt hjälpmedel vid den teoretiska behandlingen av de olika fallen. Vi bortser vid denna första principbehandling från inverkan av rör- och strökapacitanser.

    a) GK-koppling

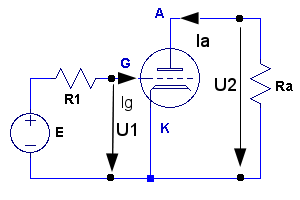
    Förstärkarstegets schema ur signalsynpunkt framgår av fig. F1.4 och motsvarande ekvivalenta småsignalschema av fig F1.5. Steget matas av en generator med komplexa emk:n E och inre resistansen R₁. Anodbelastningen utgöres av resistansen R_a.

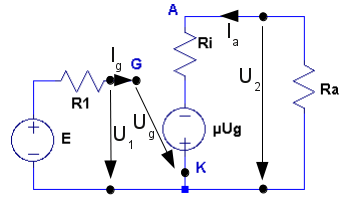Fig. F1.4.	Fig. F1.5.

    Låt oss beräkna stegets spännings-, ström- och effektförstärkning samt stegets in- och utimpedans.
    För schemat fig. F1.5 gäller:

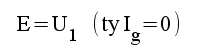	F1.7
	F1.8
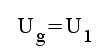	F1.9
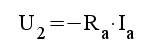	F1.10

    Komplexa spänningsförstärkningen F erhålles ur de tre sista ekvationerna efter eliminering av U_g och I_a.

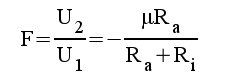   Min kommentar är: att om

    Jämför med sid. C2.26, där vi som exempel på ekvivalenta schemats användning redan beräknat storheten F.

    Stegets komplexa strömförstärkning blir

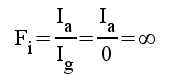    Stegets effektförstärkning blir

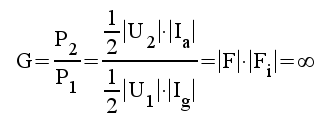    Stegets komplexa inimpedans blir

    Elimineras U_g och U₁ ur ekvationssystemet ovan erhålles

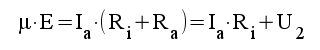Detta samband kan tolkas som ekvationen för följande ekvivalenta utgångskrets, där E_ut = μE och Z_ut = R_i.

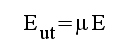	Fig. F1.6. Stegets ekvivalenta utgångskrets.

    Belastningen R_a känner sig alltså matad av en emk E_ut med inre impedansen Z_ut. Z_ut benämner vi stegets komplexa utimpedans, som i detta fall är reell och lika med rörets inre resistans R_i.

Sammanfattning GK-koppling:

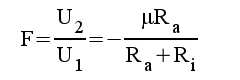	F1.11
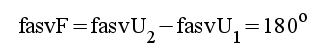	F1.12
	F1.13
	F1.14
	F1.15
	F1.16

    GK-koppling kan sägas vara elektronrörets normala förstärkarkoppling. Man får stor förstärkning (), mycket stor inimpedans samt måttlig till stor utimpedans (beroende på rörtyp). Vi observerar speciellt, att stegets fasvridning är 180º.

Övning: Hur stor blir stegets förstärkning, om man använder den matningsmetod, som anges av fic C10c, och om
    a) Rk ur signalsynpunkt överbryggas av en kapacitans Ck, vars reaktans antages försumbart liten,
    b) Rk ej överbryggas av en kapacitans ? (se Concertina)
Övning: Vilken blir stegets inimpedans (matningsmetod enligt ovan)?

    b) GG-koppling

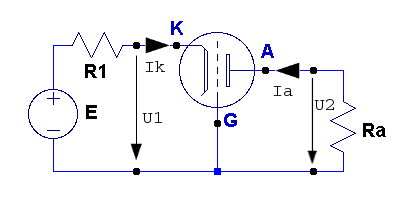
    Växelströmsschema och ekvivalentschema framgår av nedanstående fig. F1.7 och F1.8.

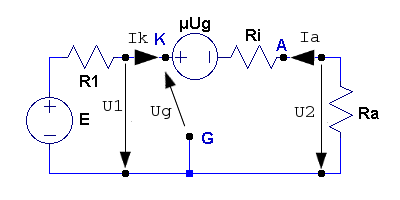Fig. F1.7.	Fig. F1.8.

    Med hänvisning till fig. F1.8 får vi följande ekvationer:

	F1.17
	F1.18
	F1.19
	F1.20
	F1.21

    Läsaren härleder ur ekvationssystemet ovan uttrycken för komplexa förstärkningen.

    Använd F1.18 bryt ut Ug:


   Byt U_g mot -U₁ och I_a mot U₂/R_a:


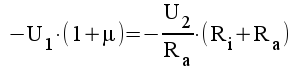   Vi får då:


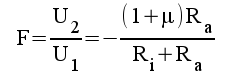   Av sambandet F1.20 följer direkt, att stegets komplexa strömförstärkning blir:


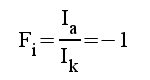   Effektförstärkningen blir därför:


   Eliminering av U_g, U₁ och I_k ur ekvationssystemet ovan ger sambandet:


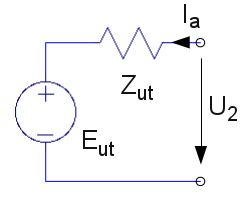
som kan tolkas som ekvationen för följande ekvivalenta utgångskrets.

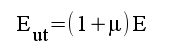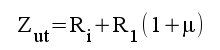	Fig. F1.9. Stegets ekvivalenta utgångskrets.

    Stegets komplexa inimpedans blir

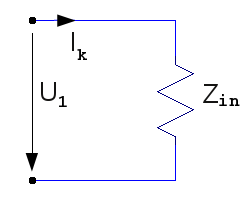
d.v.s stegets ekvivalenta ingångskrets blir följandeschema:

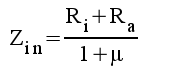	Fig. F1.10. Stegets ekvivalenta utgångskrets.

    Sammanfattning GG-koppling:

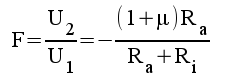	F1.22
	F1.23
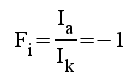	F1.24
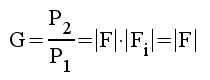	F1.25
	F1.26
	F1.27

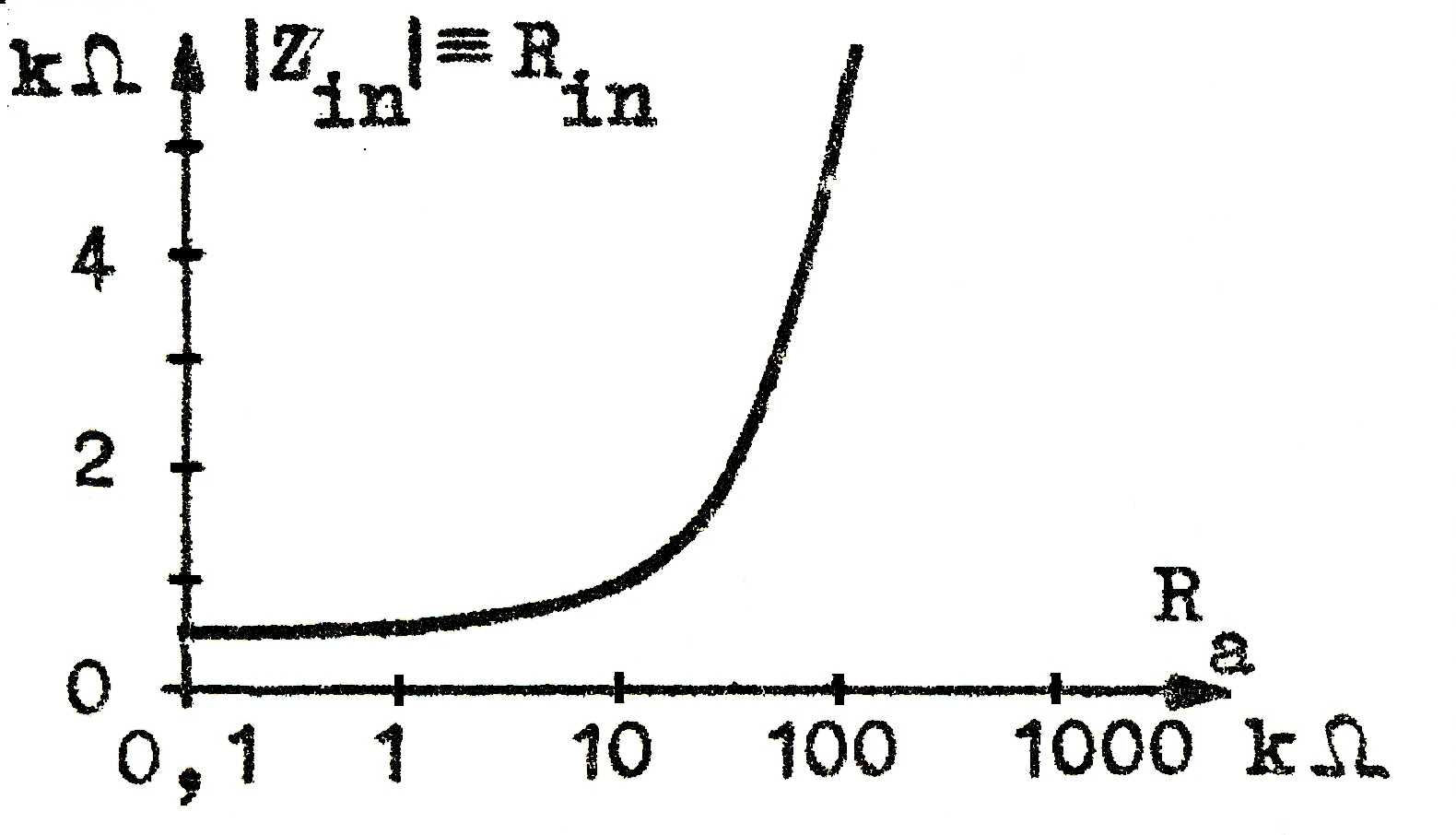
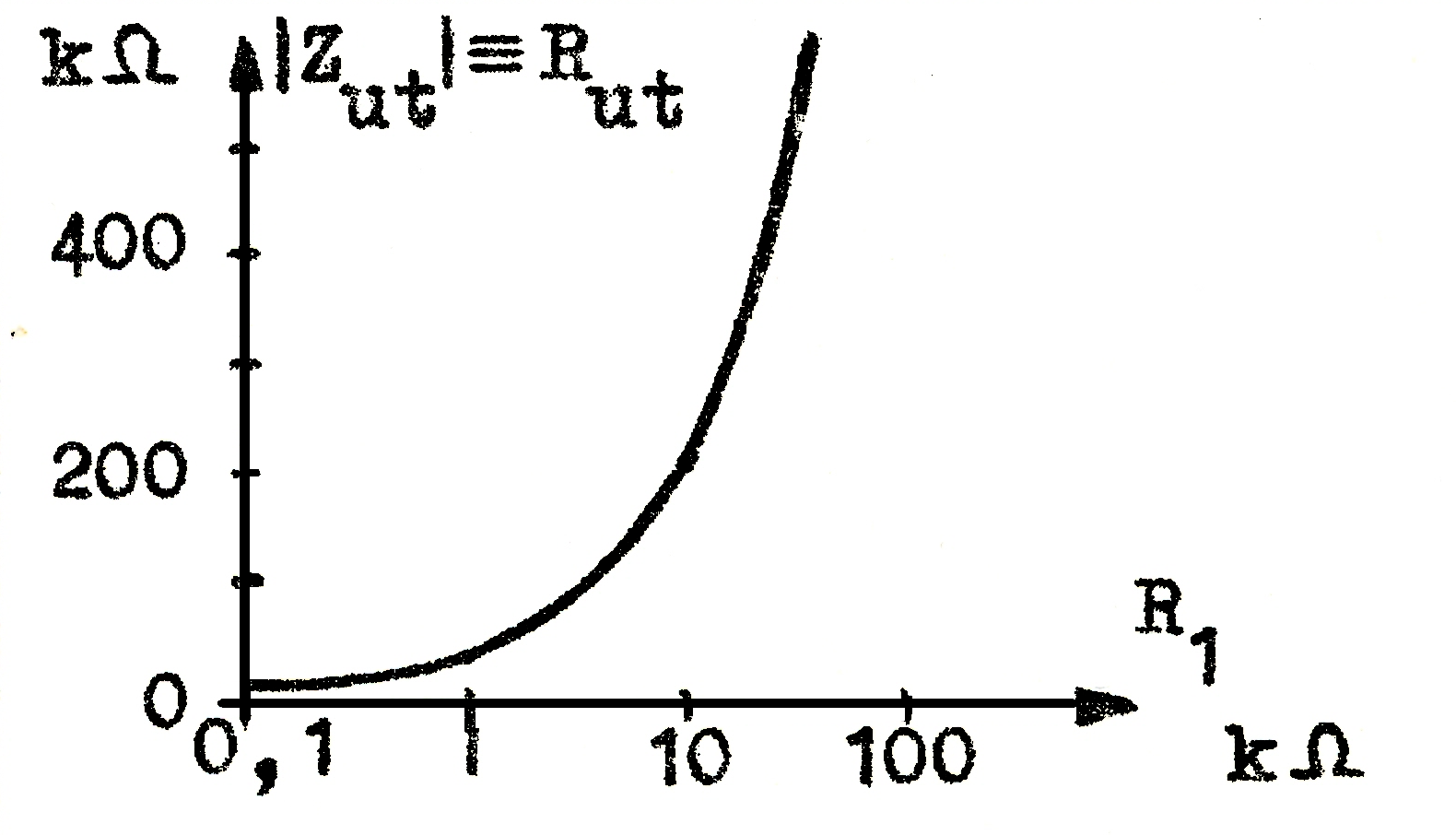
Steget har i jämförelse med GK-steget ungefär samma spänningsförstärkning men 0 fasvridning. Utimpedansen, som är stor, beror av den matade generatorns inre resistans R₁, och inimpedansen, som är låg, beror av belastningen Ra. Se härtill fig. F1.11 och F1.12 (µ=20 och R_i=20kohm) är de parametervärden, som använts vid representationen; rörets vilopunkt förutsätts givetvis oberoende av R₁ och R_a.

Fig. F1.11.    |Zin| = f(Ra).		Fig. Fx.x. texFig. F1.12.  |Zut| = f(R1).

Övning: Rita det GG-kopplade stegets praktiska schema, d.v.s. likströmsmatning skall inkluderas.

    c) GA-koppling

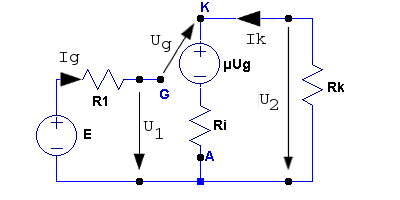Fig. F1.13.	Fig. F1.14.

För schemat i fig. F1.14 får vi följande system av ekvationer.

figur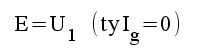	F1.28
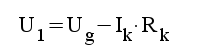	F1.29
	F1.30
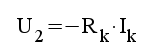	F1.31

    Stegets komplexa förstärkning blir (härledning)

    Tydligen blir 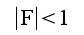 och som teoretiskt gränsfall (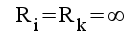) erhålles .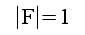
    Eftersom  erhålles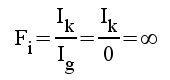

    Effektförstärkningen blir

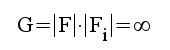    Stegets komplexa inimpedans blir

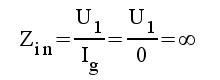    Elimineras U₁, U_g och U₂ ur ekvationssystemet ovan erhålles (härledning)

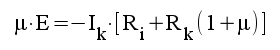som med ledning av sambandet F1.31 även kan skrivas

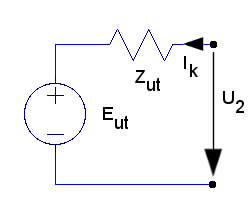
    Detta samband kan tolkas som ekvationen för följande ekvivalenta utgångskrets.

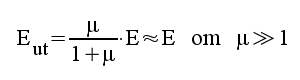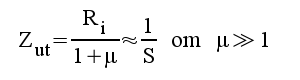	Fig. F1.15. Stegets ekvivalenta utgångskrets.

    Sammanfattning GA-koppling:

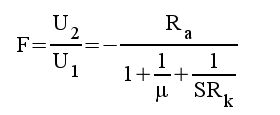	F1.32
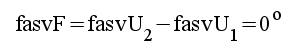	F1.33
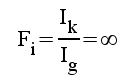	F1.34
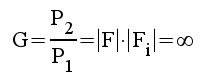	F1.35
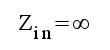	F1.36
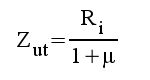	F1.37

    GA-steget ger ingen spänningsförstärkning men ger däremot ström- och effektförstärkning. Eftersom │F│≈ 1 och fasvF = 0 kommer stegets utsignalspänning (katodsignalspänning) att approximativt överensstämma med stegets insignalspänning. (utsignalen "följer" insignalen). Av denna orsak benämnes steget vanligen katodföljare. Stegets stora betydelse ligger framför allt i dess även i praktiken stora inimpedans och låga utimpedans.

    Vi har därmed skaffat oss en allmän överblick över grundkopplingarnas väsentliga egenskaper och vi skall nu övergå till ett mera detaljerat studium av olika förstärkartyper.

link >