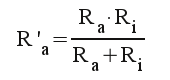< link link link >

    Rörets vilopunkt bestämms ur sambanden

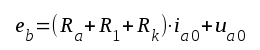	F2.1
	F2.2

på det sätt, som genomgåtts i avsnitt C2.02 (sid. C2.7). Värdetrion uaoo, i_a00 och u_g00 är vilopunkte, då röret har enbart likspänningar på sina elektroder. På grund av rörkurvernas krökning kan i drift (med signalspänningar) likriktning uppstå (se avsnitt E1.03, sid E1.8), vilket kan förorsaka viss liten förskjutning av vilopunkten. I steg, som arbetar med små amplituder, är denna förskjutning utan betydelse.
    Sedan vilopunkten fastlagts, kan rörets småsignalparametrar bestämmas på det sätt, som genomgåtts i avsnitt C2.06 (sid. C2.16), eller eventuellt direkt hämtas ur rörfabrikantens datablad. Beträffande valet av vilopunkt får vi anledning att återkomma.

    Vårt problem är nu att beräkna stegets småsignal-spänningsförstärkning som funktion av signalfrekvensen. Steget utgör en relativt invecklad konfiguration av kretskomponenter, vilket kommer att göra beräkningen både tidsödande och oöverskådlig. En inspektion av förstärkarens schema visar, som tidigare nämnts, att C₀ (vars storlek vi har frihet att välja) huvudsakligen bör inverka vid låg frekvens, medan C_a och C_g (som är förhållandevis små rör- och ledningskapacitanser) bör inverka först vid en relativt sett hög frekvens. Man bör därför rimligtvis kunna uppdela undersökningen i tre delar, var och en med sitt delfrekvensområd, d.v.s. vi kan här liksom i fråga om tonfrekvenstransformatorn tala om låg, medelhög och hög frekvens. Med medelhög frekvens menar vi då en frekvens, som är så hög, att C₀ kan anses som en kortslutning, men samtidigt så låg, att C_a:s och C_g:s inverkan kan försummas. Åtminstone tills vidare förutsätter vi, att C_k:s och C₁:s reaktanser är försumbart små vid alla aktuella frekvenser.

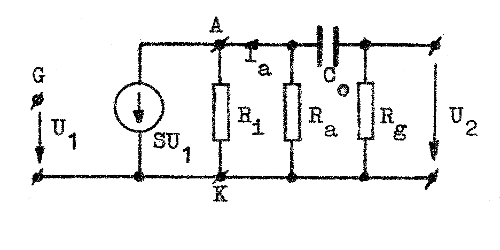
    Under de ovan nämnda förutsättningarna får vi följande ekvivalenta småsignalschema vid låg, medelhög och hög frekvens (jämför tonfrekvenstransformatorns behandling i avsnitt B6.06, sid. B6.7).

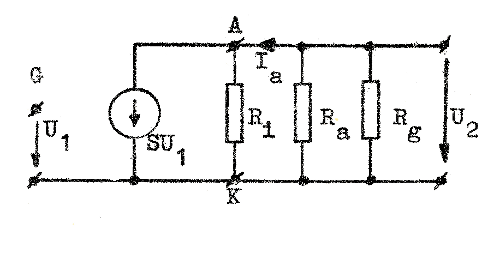
Fig. F2.2 Småsignalschema vid låg frekvens.	Fig. F2.3 Småsignalschema vid medelhög frekvens.

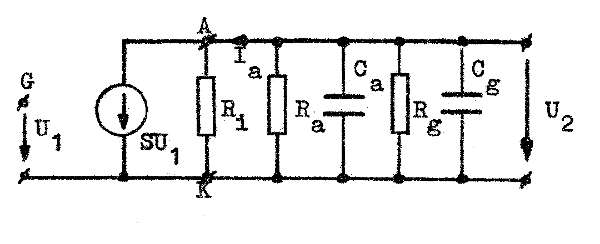		I samtliga schemor ligger rörets inre resistans Ri parallellt med R'a, varför vi inför beteckningen F2.3
Fig. 2.4 Småsignalschema vid hög frekvens.

    Av liknande skäl inför vi storheten

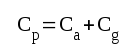F2.4

    C_p är  alltså total fördelad och till anodbelastningen parallellställd kapacitans. I fig. F2.3 och F2.4 är det vidare praktiskt att införa beteckningen Rp ("parallellresistansen") för resulterande resistansen till R_i, R_a och R_g d.v.s

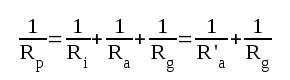F2.5

    Med dessa beteckningar förenklas våra ekvivalenta schemor ytterligare (se fig. F2.5).

Fig. F2.5 Det RC-kopplade förstärkarstegts ekvivalenta småsignalschema vid låg, medelhög och hög frekvens.

    Låt oss så i tur och ordning undersöka förstärkarstegets egenskaper inom de tre delfrekvensområden, som vi ovan definierat.


    Ur schemat fig. F2.5 erhålls direkt

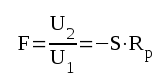som även kan skrivas

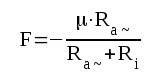, där

    Jämför detta uttryck på F med sambandet F1.11 (sid. F1.6).
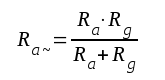    Vi inför i fortsättningen beteckningen  för spänningsförstärkningen vid medelhög frekvens.

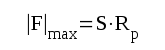F2.6

    Sammanfattningen för medelhög frekvens:

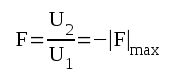	F2.7
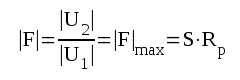	F2.8
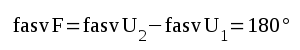	F2.9

    Av schemat fig. F2.3 framgår, att
    För motsvarande momentanvärden (u₂, i_a) gäller därför, att
    Om vi med u_a00 och i_a00 betecknar anodspänningens och anodströmmens vilovärden, så blir totala anodspänningen respektive totala anodströmmen (jämför avsnitt C2.07, C2.17):

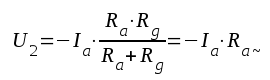
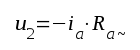
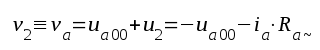
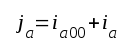
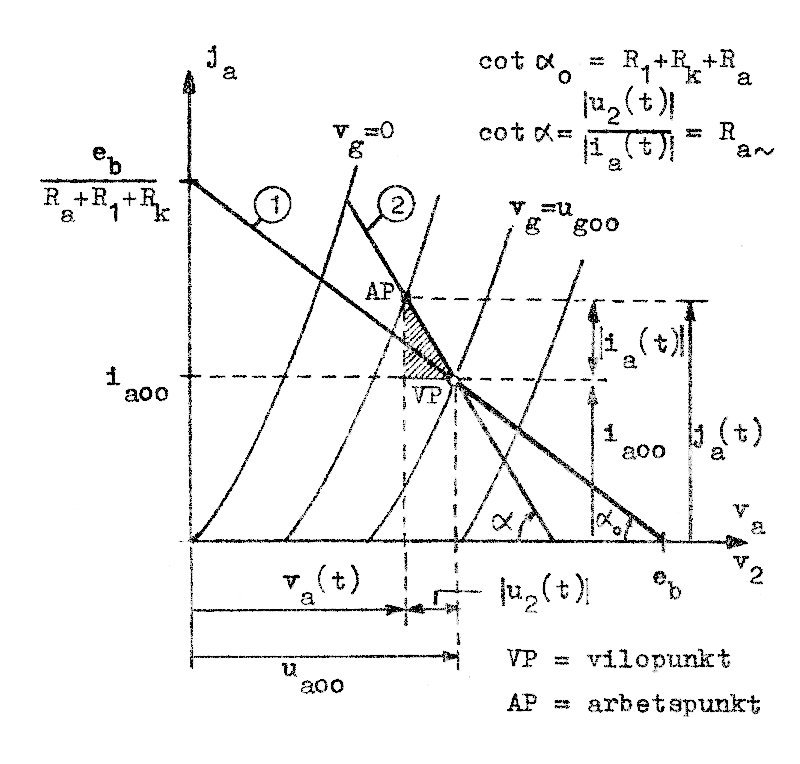		Av dessa ekvationer följer, att arbetspunkten (ja, va) i drift för sig fram och åter på linje 2, resistanslinjen för växelström, i fig. F2.6 och ej på linje 1, resistanslinjen för likström. Denna sistnämndas lutning bestämmes av totala likströmsresistansen i anodkretsen (R1+Ra+Rk, se sambanden F2.1 och F2.2). Lutningen på linje 2 däremot bestämmes av den resistans, som ur växelströmssynpunkt är inkopplad mellan anod och katod (förutsättning: C1, Ck och C0 får anses vara kortslutningar medan Ca och Cg får anses utgöra isolation).
Fig. F2.6 Arbetspunktens rörelse i anoddiagrammet vid medelhög frekvens.

    Spänningsförstärkningen vid medelhög frekvens, 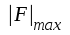, kan även bestämmas grafiskt med ledning av konstruktionen i fig. F2.6. Läsaren kan lämpligen på egen hand studera den grafiska förstärkningsbestämmningen i belysning av vad som tidigare sagts om triodens förstärkningsmekanism (se avsnitt C2.07, sid C2.17).


    Ur det lågfrekventa schemat fig. F2.5 erhålles direkt:

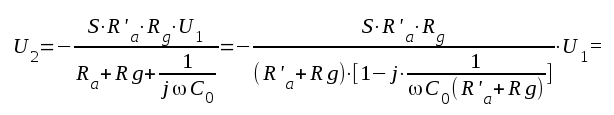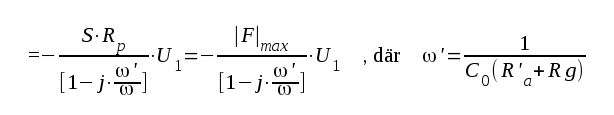    Sammanfattning för låg frekvens:

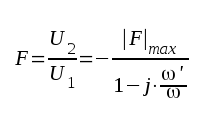	F2.10
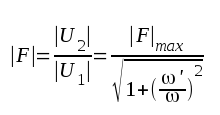	F2.11
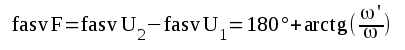	F2.12

    Vid frekvensen 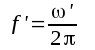 har tydligen spänningsförstärkningen nedgått till  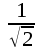av sitt maximala värde (värdet vid medelhög frekvens). Frekvensen f ' benämner vi stegtes undre gränsfrekvens, som bestämmes av sambandet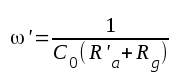

F2.13

    F2.13 kan även skrivas

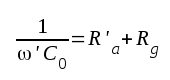F2.14

som inbjuder till följande minnesregel: Om man i ekvivalentschemat (Fig F2.5 går runt maskan C₀-R_a'-R_g är vid undre gränsfrekvensen reaktansens belopp lika med summan av resistanserna i maskan.

Övning: Utefter vilken kurva i ja-va-diagrammet rör sig arbetspunkten i drift vid låga frekvenser? Är grafisk konstruktion och grafisk förstärkningsbestämmning lämplig metodik vid låga frekvenser?


    Med ledning av högfrekvensschemat i fig. F2.5 erhålles:

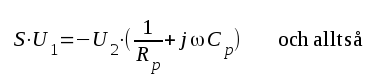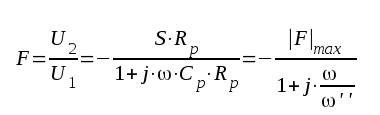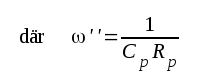F2.15

    Sammanfattning för hög frekvens:

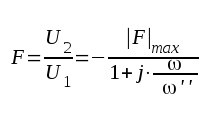	F2.16
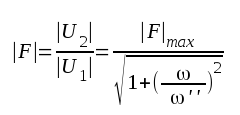	F2.17
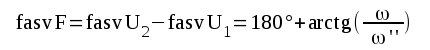	F2.18

    Vid frekvensen 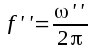 har ånyo spänningsförstärkningen nedgått till  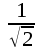av sitt maximala värde. Frekvensen f '' benämner vi stegets övre gränsfrekvens, som bestämmes av sambandet F2.15 ovan. Detta samband kan även skrivas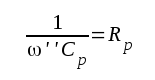

F2.19

    F2.19 kan vi i ord tolka som följande minnesregel: Om man i ekvivalentschemat (Fig. F25) går runt maskan C_p-R_p är vid övre gränsfrekvensen reaktansens belopp lika med resistansen, d.v.s. en regel helt analog med motsvarande regel vid undre gränsfrekvensen.

    Med utgångspunkt från det fullständiga schemat i fig. F2.1 kan man (om inverkan av C_k och C₁ alltjämt försummas) visa, att maximal förstärkning inträffar vid vinkelfrekvensen ω₀, bestämd av sambandet

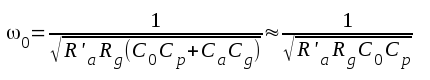F2.20

ty C₀C_p >> C_aC_g. Av uttrycken på ω' och ω'' följer, att

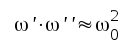F2.21

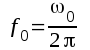    Maximal förstärkning erhålles alltså vid en vinkelfrekvens ω₀ , som är medelproportional till ω' och ω''. Frekvensen  bör sålunda benämnas medelhög frekvens. Sambandet F2.21 gäller som vi tidigare sett även för svängningskretsar och tonfrekvenstransformatorer. Lägg även märke till att vid gränsfrekvensen är fasvridningen ±45° relativt värdet vid medelhögfrekvens (180°).

    >Om man så vill kan man sammanfatta F2.7, F2.10 och F2.16 i ett samband, giltigt vid alla frekvenser:

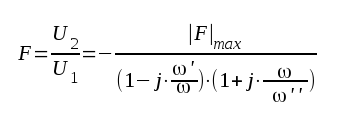F2.22

    Vid låga frekvenser är nämligen ω/ω'' << 1 och sambandet F2.22 övergår då approximativt i sambandet F2.10. Vid höga frekvenser är ω'/ω << 1 och F2.22 övergår då approximativt i F216. Sätter man slutligen i F2.22 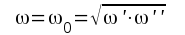 erhålles


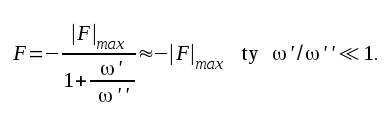link >