< link link link >

    Förstärkarestegets komplexa spänningsförstärkning är kvoten mellan stegets komplexa utsignalspänning (utstorhet) och stegets komplexa insignalspänning (instorhet) och kan därför sägas vara stegets överföringsfunktion (jämför sid. F1.1). Ett överskådligt sätt att representera ett förstärkarstegs (eller allmänt ett systems) frekvenskarakteristik är i form av kurvor över överföringsfunktionen som funktion av frekvensen.
Överföringsfunktionen F är emellertid en komplex storhet, d.v.s. vi har

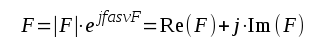    Vi kan därför tänka oss två olika möjligheter att representera storheten F. En metod är att rita upp kurvor över F och fasvF var för sig som funktion av frekvensen eller vinkelfrekvensen (se fig F2.7 och F2.8, där som exempel följande värden valts vid representationen:
ω' = 1000 rad/s, ω'' = 100000 rad/s,  ).

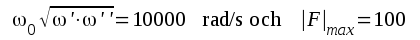Fig. F2.7 RC-kopplade förstärkarstegets förstärkning som funktion av signalfrekvensen.

    Lägg i fig. F2.7 märke till att ω0 ingalunda hamnar mitt emellan ω' och ω'' på frekvensaxel, eftersom ω0 är geometriska medelfrekvensen till ω' och ω''.

Fig.  F2.8.  Det RC-kopplade förstärkarstegets fasvridning som funktion av signalvinkelfrekvensen.

    Denna representationsmetod är den normala, men användes vanligen i en något modifierad form, som går under benämningen Bode-diagram (se följande avsnitt 2.05). I detta diagram, som omfattar såväl beloppskurvan (amplitudkurvan) som faskurvan, avsättes fasvF och F i logaritmiskt mått som funktion av vinkelfrekvensen w, ävenledes i logaritmiskt mått.

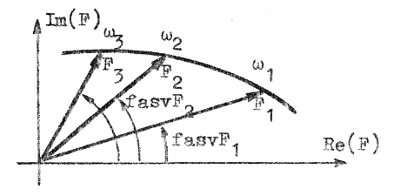
    En annan representationsform är det s.k. Nyquist-diagrammet, i vilket F redovisas som visare i ett komplext talplan (F-planet). Med ledning av sambandet F2.22 (eller F2.7, F2.10 och F2.16) kan vi rita det ovan behandlade förstärkarstegets Nyquist-diagram (ortsdiagram), d.v.s. den kurva, som den komplexa förstärkningsvisarens spets beskriver i komplexa talplanet, då ω genomlöper alla värden från 0 till x. Man väljer olika frekvensvärden ω1, ω2, ω3....... och beräknar (eller mäter experimentellt) motsvarande absolutbelopp F1, F2, F3 ....... och fasvinklar fasvF1, fasvF2, fasvF3....... samt uppritar motsvarande visare i ett komplext talplan (se fid. F2.9). Väljes frekvensvärdena tillräckligt tätt, är det lätt att genom



visarspetsarna rita den kurva, som spetsen på visaren F följer, då varje ω varieras. Nyquist-diagrammet har ingen frekvensskala, varför frekvensvärdena, om dessa önskas redovisade, måste markeras på kurvan.
Fig. F2.9. Nyquist-diagramets konstruktion.

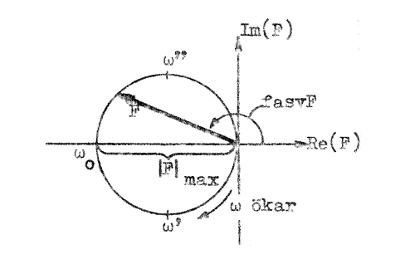
    Representeras sambandet F2.22 på beskrivet sätt, finner man, att Nyquist-diagrammet för vårt ovan behandlade förstärkarsteg blir en cirkel



i övernsstämmelse med fig. F2.10. Vinkelfrekvenserna ω' , ω0och ω'' har i diagrammet speciellt markerats.

Övning: Hur ser Nyquist-diagrammet ut, om man antager, att kopplingskondensatorn (C0) har reaktansen noll vid alla frekvenser.
Fig. F2.10 Det RC-kopplade förstärkarstegets Nyquist-diagram.


link >