< link link link >

Som nämts i avsnitt 2.04 ovan utgör Bode-diagrammet en grafisk representation av överföringsfunktionen (komplexa förstärkningen) F, där

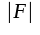och fasvF var för sig redovisas som funktion av frekvensen ω.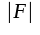

och ω anges i logaritmiskt mått och fasvF i grader eller radianer. Logaritmiskt mått för

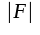har bland annat den fördelen, att en multiplikation av olika överföringsfunktioners belopp ersättes av en addition. Som logaritmiskt mått för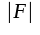

användes decibel (beträffande begreppet decibel, dB, se avsnitt A7). En kaskadkoppad förstärkares totalförstärkning i dB erhålles sålunda som summan av de enskilda stegens förstärkning i dB. Överföringsfunktionen behöver givetvis ej vara en komplex förstärkning, men vi specialiserar i detta sammanhang på vårt ovan behandlade motståndskopplade förstärkarsteg.

Om spänningsförstärkningen är

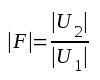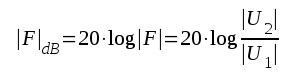definerar vi spänningsförstärkningen i dB som

F2.23

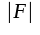= 1 är

= 0, om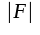

= 10 är

= 20, om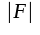

= 100 är

= 40 o.s.v..
För vårt ovan behandlade motståndskopplade förstärkarsteg erhålles ur sambandet F2.22:

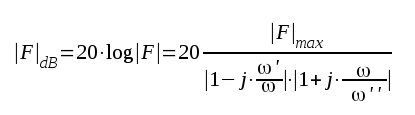F2.24

eller

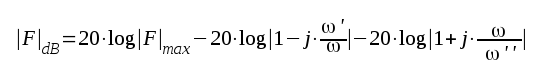F2.25

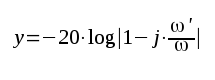Första termen i F2.25 är en konstant. Låt oss studera andra termen, som vi tillfälligt betecknar med y, d.v.s vi har

	F2.26
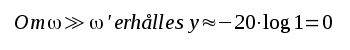	F2.27
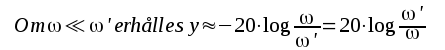	F2.28
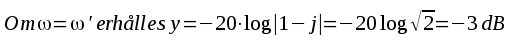	F2.29

Låt oss nu rita termen

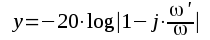som funktion av x = logω
Vid uppritningen har vi stor hjälp av sambanden F2.27 - F2.29. I ett x-y-koordinatsystem representeras F2.27 av en horisontell, rät linje (linjen a i fig. F2.11), som sammanfaller med x-axeln.

F2.28 skriver vi på följande sätt

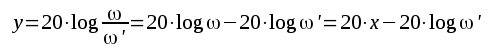F2.30

d.v.s F2.30 representerar en rät linje, som har positiv lutning och som skär x-axeln i punkten x=logω' (linjen b i fig. F2.11). Med ledning av dessa "hjälplinjer" kan y lätt skisseras, ty, om ω >>ω', närmar sig y linjen a (enligt F2.27) och om ω<<ω', närmar sig y linjen b (enligt F2.28). Om ω=ω' ligger y i punkten c (enligt F2.29). Det verkliga utseendet på y kan alltså lätt skisseras, ty

		den verkliga kurvan skall gå genom punkten c och vidare är tydligen linjerna a och b kurvans asymptoter vid höga respektive låga frekvenser. På analogt sätt leder sista termen i sambandet F2.25 till en representation i enlighet med fig. F2.12
Fig. F2.11

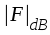I fig. F2.13 slutligen har samtliga tre termer (jämte asymptoter) i sambandet F2.25 inritats. Eftersom spänningsförstärkningen i dB,

, enligt F2.25 är summan av dessa tre termer, kan vi nu lätt rita såväl en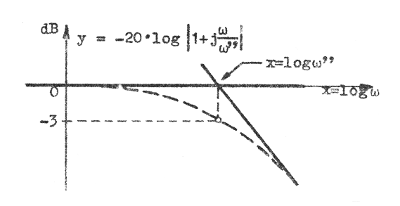

		av räta stycken sammansatt kurva, den s.k. asymptotiska beloppskurvan (asymptotkurvan), som den verkliga beloppskurvan (fig. F2.14)
Fig. F2.12

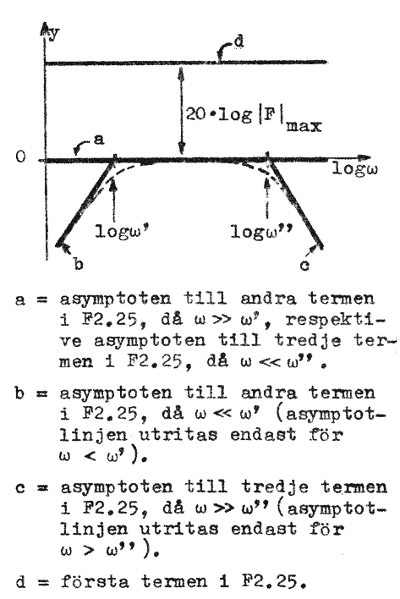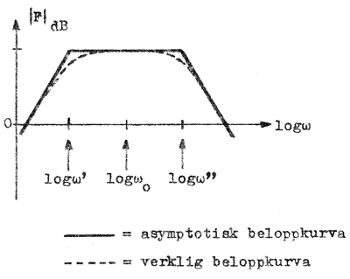	Fig. F2.14. Summakurva till fig. F2.13. Eftersom ω²₀ = ω' x ω'' blir Medelhög frekvens ligger därför på den logaritmiska frekvensaxeln mitt emellan ω' och ω''. Den asymptotiska kurvan är "bruten" vid vinkelfrekvenserna ω' och ω''.
Fig. F2.13

Motsvarande frekvenser benämnes därför brytfrekvenser. Asymptotkurvans brytfrekvenser är i detta fall förstärkarstegets gränsfrekvenser.

Beloppskurvorna ritas lämpligen på lin-log-papper. Vår i fig. F2.7 uppritade kurva får med vårt nya representationssätt ett utseende enligt fig. F2.15 (beträffande vid representationen använda siffervärden se sid. F2.8), där den logaritmiska frekvensaxeln graderats på ett antal olika sätt, som berörs nedan.

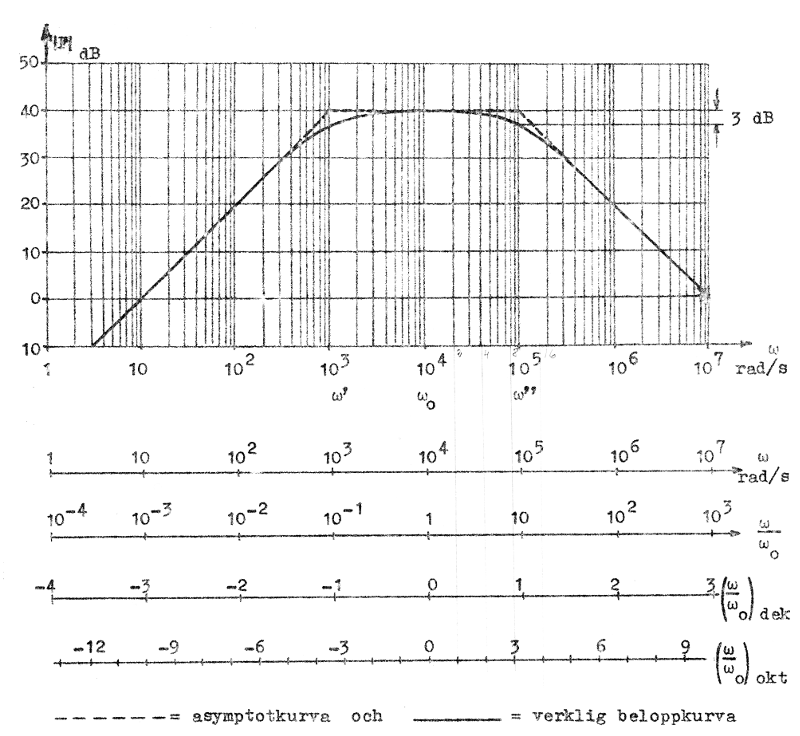Fig. F2.15 Bode-diagrammets asymptotiska och verkliga beloppskurva för ett RC-kopplat förstärkarsteg.

Normalt ingår frekvensvariabeln ω i en överföringsfunktion i termer av typen ω/ω_k, där ω_k är en för systemet karakteristisk frekvens (t.ex. en gränsfrekvens; se sambandet F2.24). Om ω är dubbelt så stor som ω_k säges w ligga en oktav över ω_k. Är ω hälften av ω_k säges ω ligga en oktav under ω_k. En oktav definieras alltså som frekvensförhållandet 2:1.

En dekad definieras på motsvarande sätt som frekvensförhållandet 10:1. Som exemplifiering har frekvensaxeln i fig. F2.15 graderats på olika sätt, varvid godtyckligt ω₀ valts som referensfrekvens. Ett frekvensförhållande uttryckt i oktaver respektive dekader skriver vi

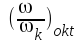och

.
Av definitionen ovan följer, att

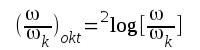F2.31

På liknande sätt erhålles

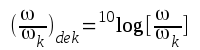F2.32

Av F2.31 och F2.32 följer, att

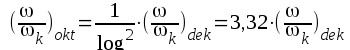F2.33

    Studerar vi nu åter fig. F2.15 observerar vi några för uppritningen värdefulla egenskaper.

    a) Vänstra delen av asymptotkurvan har lutningen 20 dB/dekad = 6 dB/oktav,
    b) Högra delan av asymptotkurvan har lutningen -20 dB/dekad = -6 dB/oktav,
    c) När ω = ω' respektive när ω = ω''ligger verkliga beloppskurvan 3 dB under asymptotkurvan.
    d) För frekvenser en oktav under eller en oktav över ω' respektive en oktav under eller över ω'' ligger den verkliga beloppskurvan 1 dB under asymptotkurvan.
    e) För frekvenser, som ligger mer än en dekad från ω' respektive ω'', sammanfaller praktiskt taget den verkliga och den asymptotiska kurvan.

    Punkterna a) - e) anger några allmängiltiga egenskaper, som gäller för överföringsfunktioner av den typ, som anges av sambandet F2.22 (överföringsfunktioner med linjära faktorer, d.v.s. faktorer av typen

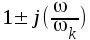men ej exempelvis av typen

).
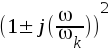Övning:

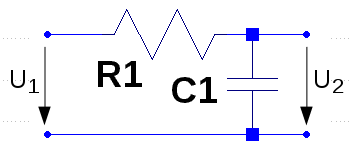Överföringsfunktionen för vidstående RC-krets är
F = U₂/U₁. Rita Bode-diagrammets asymptotkurva och verkliga beloppskurva. Vilket är uttrycket för systemets brytfrekvens?

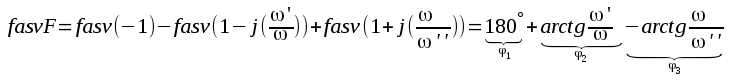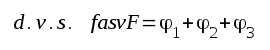Vi övergår nu till att studera Bode-diagrammets faskurva. Ur sambandet F2.22 erhålles:


	F2.34

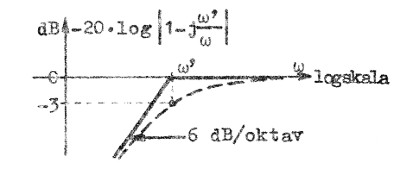Liksom beloppskurvan utgör faskurvan en summa av tre termer. Första termen i F2.34 (φ₁) är en konstant. Vi ritar andra termen (φ₂ = φ₂(ω)) med logaritmisk frekvensaxel och får då fig. F2.16 nedan. Som jämförelse ritar vi även andra termen i F2.25 (d.v.s. en upprepning av fig. F2.11).


Fig. F2.16		Fig. F2.17

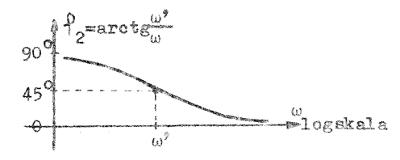
Vi observerar, att φ₂ →0, då ω>>ω', att φ₂ → 90º då ω <<ω' och att φ₂ = 45º då ω = ω'.
Ett liknande studium av tredje termen i F2.34 (φ₃ = φ₃(ω)) respektive tredje termen i F2.25 ger fig. F2.18 och F2.19 nedan.


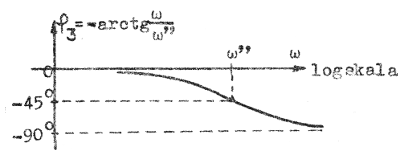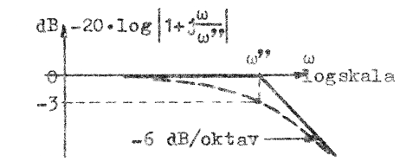Fig. F2.18		Fig. F2.19

    Vi observerar, att φ ₃→0,då ω>>ω'', att φ₃ → -90º då ω <<ω'' och att φ₃ = -45º då ω = ω''.

    Jämför man belopp- och faskurverna (fig. F2.16 och F2.17 respektive fig. F2.18 och F2.19) lägger man märke till att det tycks finnas ett samband mellan beloppkurvans lutning och fasvinkelns värde. Då beloppkurvans lutning går mot noll går fasvinkeln mot noll, då lutningen går mot6 dB/oktav går fasvinkeln mot 90º och då lutningen går mot -6 dB/oktav går fasvinkeln mot -90º. Vid brytfrekvenserna blir fasvinkeln 45º respektive -45º. Bode (vilken liksom Nyquist är matematiker vid Bell Telephone Laboratories, USA) har visat, att det, under vissa matematiska förutsättningar, finnes ett entydigt samband mellan fasvinkeln och beloppskurvans lutning. På denna fråga kan vi dock ej ingå här. Även faskurvorna kan approximeras med räta linjestycken uppbyggda asymptotkurvor.

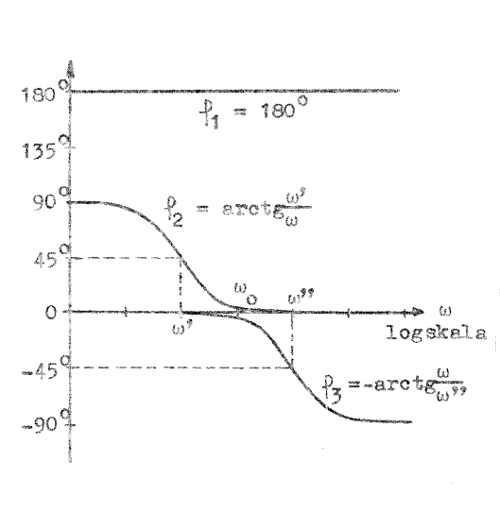
    Med ledning av fig. F2.16 och F2.18 kan vi slutligen upprita φ = fasvF, eftersom enligt sambandet F2.34 φ=φ₁ + φ₂ + φ₃, där φ₁=180º.
Se härtill fig. F2.20 och F2.21, där dels de enskilda φ-termerna presenterats, dels summatermen φ inritats.


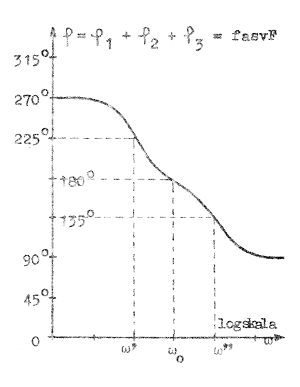Fig. F2.20	Fig. F2.21

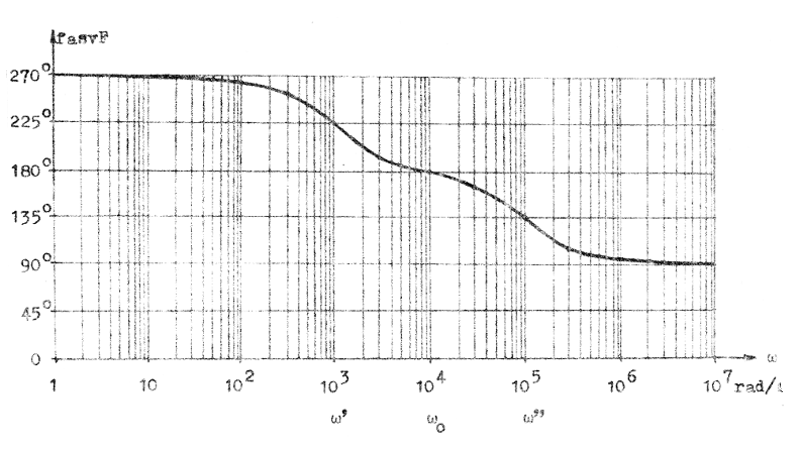Vår i fig. F2.8 uppritade faskurva får med vårt nya representationssätt följande utseende (fig. F2.22; använda siffevärden se sid. F2.8).

Fig. F2.22. Bode-diagrammets faskurva för ett RC-kopplat förstärkarsteg.

Slutligen bör påpekas, att fig. F2.15 (beloppskurvan) och fig. F2.22 (faskurvan) tillsammans utgör det RC-kopplade stegets Bode-diagram.

link >