< link link link >

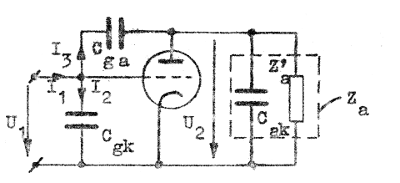
    Låt oss beräkna inimpedansen för ett GK-steg med hänsyn tagen till kapacitanserna C_gk, C_ga och C_ak. Stegets signalschema framgår av fig. F2.26 nedan.

		Stegets anodimpedans förutsätts vara Z'a. Cak ränar vi lämpligen in i anodimpedansen och betecknar totala komplexa anodimpedansen med Za. Med schemats beteckningar erhålles direkt:
Fig. F2.26.

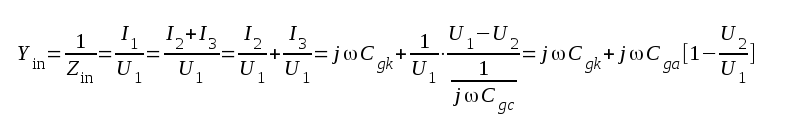
= stegets komplexa förstärkning, varför vi får:

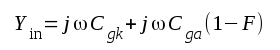F2.35

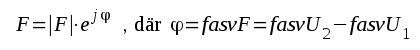Vi inför . Vi får ur sambandet F2.35:

F2.36

    Med ledning av sambandet F2.36 kan vi rita ett ekvivalent schema för inimpedansen i enlighet med fig. F2.27 nedan

Fig F2.27. Inimpedansens ekvivalenta schema.

     Om φ = 180° , vilket närmelsevis är fallet, när anodimpedansen Z_a är resistiv, blir R_in = ∞ ​​​​​​​​​​​​​​ och inkapacitansen blir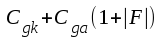, d.v.s. en kapacitans, som kan vara mångdubbelt större än Cgk.

    Om φ < 180° (kapacitiv anodimpedans) blir R_in en ordinär resistans. Om däremot φ > 180° (induktiv anodimpedans) blir R_in en negativ resistans, något som kan ge upphov till instablitet (självsväning) i ett förstärkarsteg.

    Vid resistiv anodimpedans har vi alltså:

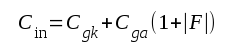F2.37

    Egenskapen att anod-galler-kapacitansen (anod-galler-admittansen) från ingången set blir multiplicerad med faktorn 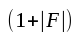 benämnes Miller-effekten. Egenskapen i fråga kan i vissa kopplingar utnyttjas praktiskt, i andra är den en källa till besvär.
    För en triod är såväl C_gk som C_ga av storleksordningen någon eller några pF. Trioden ECC83 har exempelvis C_gk = 1,6 pF, C_ga = 1,7 pF och µ = 100. Om vi räknar med 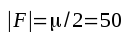skulle vi få:
    Inkapacitansen domineras som synes helt av Miller-effekten.

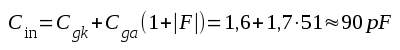    För en förstärkarpentod är C_gk av ungefär samma storleksordning som för en triod, medan C_ga är några tusendels upp till några hundradels pF.
Pentoden EF80 ( som närmast är en högfrekvenspentod) har exempelvis C_gk = 7,5 pF, C_ga < 0,007 pF och µ ≈ 4000. Om vi även här räknar med 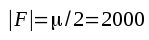 får vi:
    Trots en avsevärt större förstärkning och trots större Cgk blir den effektiva inkapacitansen här ungefär fyra gånger mindre än i triodfallet.
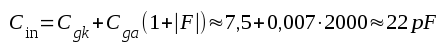    Totala parallellkapacitansen Cp i vårt schema fig. F2.5 sammansätter sig alltså i huvudsak på följande sätt:

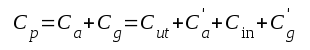F2.38

där C_ut i huvudsak är rörets C_ak, C'_a är fördelade kapacistanser från ledningar och komponenter till vänster om C₀, C_in är efterföljande stegs inkapacitans (inklusive Miller-effekt) och C'_g är fördelade kapacitanser till höger om C₀. Skall man få hög övre gränsfrekvens måste tydligen samtliga delkapacitanser i F2.38 pressas till ett minimum.

link >