I ett triodförstärkarsteg är normalt Ri < Ra < Rg, varför Ri blir bestämmandande för Rp, som i sin tur tillsammans med Cp bestämmer övre gränsfrekvensen ( se sambanden F2.5 och F2.19 ). Om triodsteget följes av ytterligare ett triodsteg blir Cp relativt stor, eftersom Miller-effekten vi trioder gör sig starkt gällande (avsnitt 2.07).
I ett pentodsteg är normalt Ri > Ra < Rg, varför Ra och Cp i huvudsak bestämmer övre gränsfrekvensen. Vid pentoder är Miller-effekten ej så utpräglad som vid trioder, varför Cp i pentodfallet kan hållas nere. Med samma S och samma övre gränsfrekvens kan därför Rp göras större än vid triodsteg, vilket medför högre förstärkning.
För ett motståndskopplat förstärkarsteg är bandbredden
 |
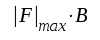 är ett lämpligt godhetstal för steget.
Vi har tidigare funnit, att
är ett lämpligt godhetstal för steget.
Vi har tidigare funnit, att 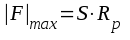 och att
och att  (se sambanden F2.6 och F2.19), varför vi får
(se sambanden F2.6 och F2.19), varför vi får 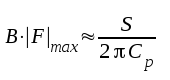 |
F2.39 |
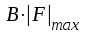 benämer
vi förstärkning-bandbredd-produkten
(Hz).
benämer
vi förstärkning-bandbredd-produkten
(Hz). Cp är ju totala parallellkapacitansen, d.v.s. Cp inkluderar fördelade kapacitanser utanför röret. Eftersom dessa varierar i olika tillämpningar, uppger rörfabrikanten ofta faktorn
 |
F2.40 |
link >