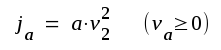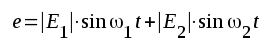Är insignalen på en förstärkare u1(t) bör utsignalen vara u2(t) = k u1(t - t0), där k är en konstant och där t0 representerar eventuell tidfördröjning av signalen vid dess passage genom förstärkaren. Signalen bör sålunda blott ändras till skalan ej till formen. Om utsignalens form ej övernsstämmer med insignalens säges förvränging eller distorsion föreligga.
Innan vi närmare går in på distorsion är det lämligt att repetera några i distorsionssammanhng viktig begrepp.
Med ett linjärt transmissionselement menar vi ett element, i vilket strömmen genom elementet är proportionell mot den påtryckta spänningen.
Exempel på dylika element är motstånd, spolar (utan järnkärna) och kondensatorer. En linjär transmissionslänk är en av linjära transissionselement uppbyggd länk, t.ex. en RC-krets eller en svängingskrets.
Andra element och länkar sägas vara olinjära, t.ex soplar och transformatorer med järnkärna, elektronrör, transistorer m.fl.. Typiskt för ett olinjärt element eller en olinjär länk är, att deras karakteristiska kurvor (magnetiseringskurvan, ia0-ua0-kurvan) är krökta kurvor. Även om den karakteristiska kurvan ej är kontinuerligt krökt utan exempelvis sammansatt av räta linjestycken säges transmissionselementet vara olinjärt (ett exempel härpå är den i fig. C1.26, sid. C1.24 angivna diodkarakteristiken). Ett olinjärt transmissionselement kan alltså vara linjärt inom ett mindre område. Arbetar elementet i detta område säges det arbeta i sitt linjära område. Egentligen är alla praktiska element och länkar olinjära, ty proportionalitet mellan ström och spänning existerar endast för begränsade värden på strömmar och spänningar. Höjes exempelvis spänningen över ett motstånd mer och mer inträffar så småningom överslag och ström-spänningskrakteristiken är ej längre linjär.
Varje periodisk ström eller spänning kan tänkas uppdelad i en summa av sinusformade strömmar respektive spänningar, vilkas frekvenser förhåller sig som hela tal och vilka har en viss inbördes faskföskutning. Är strömmens eller spänningens tidsfunktion given kan strömm eller spänningen rent matematiskt uttryckas som en trigonometrisk serie; man säger, att man utvecklat strömmen eller spänningen i en Fourier-serie (se avsnitt A8). Vet man därför hur en sinussignal överföres av enviss transmissionslänk, kan man härav draga slutsatser om hur en icke sinusformad signal överföres av länken (frekvensanalys). En icke sinusformad signal kan alltså sägas innehålla olika delfrekvenser, som tillsammans upptager ett visst frekvensutrymme, d.v.s. transmissionslänken måste för att kunna överföra signalen ha en viss bandbredd.
Man skiljer mellan två huvutyper av distorsion, linjär distorsion och olinjär distorsion.
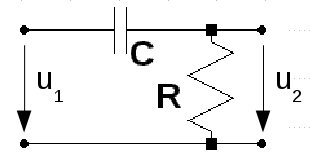
Linjär distorsion uppstår, där alla transmissionslänkar är linjära men har frekvensberoende transmissionsegenskaper. Tag som exempel en RC-krets enligt fil. F2.32. Om u1 är en sinusspänning vlir även u2 en sinusspänning och vi har i komplex form:
 |
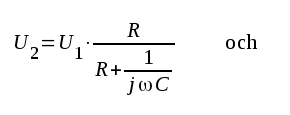 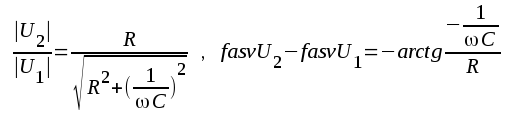 |
|
| Fig.F2.32 |
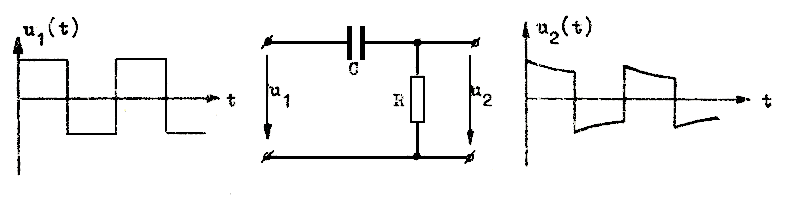 |
| Fig. F2.33 Linjär distorsion i RC-länk |
I vårt ovan behandlade motståndskopplade förstärkarsteg har vi hittills förutsatt små signaler, vilket innebär, att röret arbetar på krakteristikens linjära delar och förstärkarsteget som helhet kan därför sägas arbeta i huvudak linjärt. Om emmellertid undre gränsfrekvensen valts alltför hög och övre gränsfrekvensen alltför låg kommer vi tydligen att få en linjär distorsion, som yttrar sig i att bas och diskant undertryckes och vi får en icke naturtrogen återgivning av exempelvis musk. Liknande egenskaper hari vi tidigare även observerat i samband med tonfrekvenstransformatorns linjära teori.
Olinjär distorsion förorsakas av olinjära transmissionselement och länkar. Distorsion av denna typ är den besvärligaste och vi kan av det föregående förstå, att den förorsakar de största problemen i transmissionslänkar (t.ex. förstärkare), som arbetar med stora ampliturer (slutsteg).
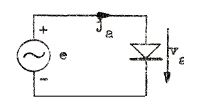
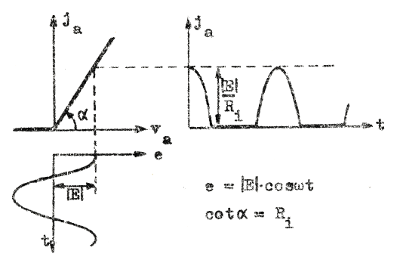
Olinjär distorsion behandlas enklast, om man utgår från sinusformad insignal och upplöser utsignalen i en Fourier-seris (spektral upplösning). Låt oss som exempel undersöka den som utsignal betraktade strömmen ja i en enkel diodkrets (fig. F2.34), som påtryckes en rent sinusformad insignal e = .... Dioden förutsättes för enkelhets skull var linjär för positiv anodspänning och krakteriseras däför av sin inre resistans Ri (se sid. C1.23, avsnitt C1.09).
 |
Strömmen ja består av en serie sinushalvor och distorsionen är alltså i det valda exemplet utpräglad (fig. F2.35). Vi upplöser strömme ja i ett spektrum (utvecklar ja i en Forier-serie). Serien får följande allmäna form: | |
| Fig.F2.34 |
 |
F2.63 |
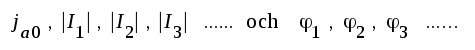 är konstanter,
som kan beräknas (se avsnitt A8). I vårt fall får serien
formen
är konstanter,
som kan beräknas (se avsnitt A8). I vårt fall får serien
formen
 |
F2.64 |
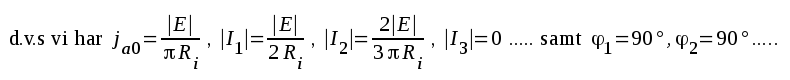 |
 |
I vårt betraktade fall är distorsionen
sådan, att en likströmsterm uppståt (riktströmmen
ja0). Vi säger då, att vi fått
likriktning och transmissionselementet
(dioden) säges ha ventilverkan, något
som vi praktiskt utnyttjar i likriktare (kapitel
E). Som ett mått på den olinjära distorsionen brukar man i tonfrekvenstekniken använda klirrfaktorn k, ett obenämnt tal, definierat av sambandet |
|
| Fig.F2.35 |
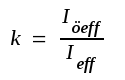 |
F2.65 |
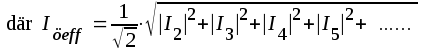 = de icke
önskvärda delsvängningarnas (övertonernas) effektivvärde
(se avsnitt A8) och där
= de icke
önskvärda delsvängningarnas (övertonernas) effektivvärde
(se avsnitt A8) och där svängningarnas (övertonernas) effektivvärde (se avsnitt A8) och där
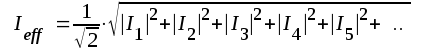 =
effektivvärdet av samtliga delsvängingar.
=
effektivvärdet av samtliga delsvängingar.Har vi ingen olinjär distorsion blir tydligen k = 0.
Man brukar även definiera en övertonsfaktor d samt deltonsfaktorer dn genom sambanden
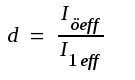 och och
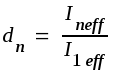 (N=2,
3, 4..) (N=2,
3, 4..) |
F2.66 F2.67 |
k, d och dn brukar normalt uttryckas i procent.
I vårt ovan skisserade diodfall får vi
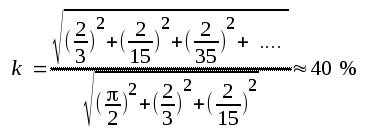 |
|
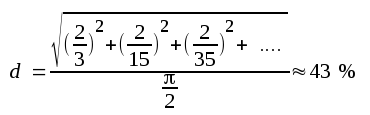 |
|
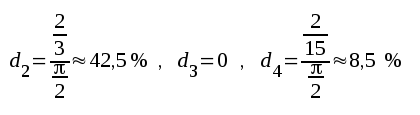 |
Vi har ovan valt ett extremt exempel, där distorsionen är avsevärd. I ett ordinärt effektförstärkarsteg för tonfrekvens är vid sinusformad insignal klirrfaktorn vanligen <10 %, då steget lämnar full uteffekt. I spänningsförstärarsteg för små amplituder, d.v.s. i huvudask linjärt arbetande steg av den typ vi i avsnitt F hittills behandlat, är klirrfaktorn avsevärt lägre. I dylika fall kan den olinjära distorsionen vanligen helt förummas.
Klirrfaktorn och övertonsfaktorn kan inte undera alla omständigheter sägas var ett lämpligt distorsionsmått. Den ovan behandlade olinjära distorsionen säges var harmonisk (de uppkomna delsvängningarnas frekvenser är multipler av en grundfrekvens). Vi kan i vissa fall även få oharmonisk olinjär distorsion (de uppkomna delsvängningarna innehåller även adra frevkenser än multipler av insignalen frekvenser). Låt oss
 |
som exempel studera
kopplingen i fig. F2.36, där ventilen antages ha
kvadratisk krakteristik, d.v.s. ventilkurvan kan
beskrivas av ett samband av typen
där a är en konstant. Låt i Fig. F2.36 e vara insignalen och ja utsignalen och låt vidare
där ω1 och ω2 är två icke harmoniska frekvenser (ej heltalsmultipler av varandra). |
|||||
| Fig.F2.36 |
Enligt Kirschoffs lag II är i fig. F2.36
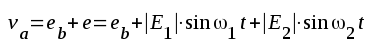 |
F2.70 |
Om vi förutsätter, att
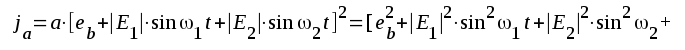 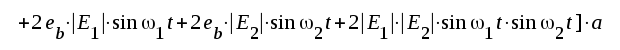 |
F2.71 |
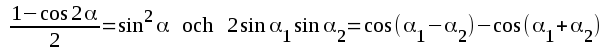 |
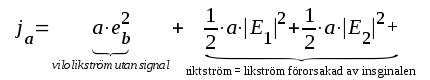 |
|
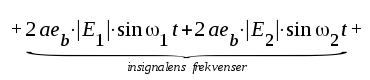 |
|
 |
|
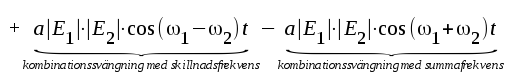 |
F2.72 |
Med hjälp av s.k. våganalysatorer kan man på experimentell väg bestämma fourierkoefficienterna (de olika deltonernas amplitud) hos ett periodiskt ström- elller spänningsförlopp. En våganalysator är i princip en selektiv rörvoltmeter, vars mätfrekvens är avstämbar exempelvis inom tonfrekvensområdet. Vid analys av en signalspänning avstämmes analysatorn först till grundonen och dess spänning uppmätes. Genom avstämning till de olika överonernas frekvenser kan man uppmäta deslspänningarna en efter en.
En annan möjlighet är att fotografera eller avrita den periodiska strömmens eller spänningens oscillogram och därur med hjälp av grafisktmatematiska metoder bestämma fourierkoefficienterna.
Klirfaktorn k kan relativt lätt bestämmas med en enkel s.k. klirrfaktorbrygga. Fig. F2.37 är ett exempel på en dylik (Siemens).
 |
| Fig F2.37. Siemens klirrfaktorbrygga. |
1. Omkopplaren ställes i läge I. En spänning av grundfrekvens (ω) inmatas mellan A och B, varefter r och C injusteras spå, att rörvoltmetern visar noll. Då är bryggan i balans för grundtonen d.v.s. ωL = 1/ωC och rL + r = R2.
2. Den spänning, som skall undersökas, inmatas mellan A och B. Visar rörvoltmetern alltmämt noll är klirrfaktorn k = 0. Om rörvoltmetern visar värdet UReff gäller (om totala reaktansen i LC-grenen kan anses mycket stor för frevenserna 2ω, 3ω, 4V .....) att
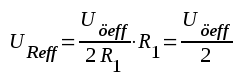 |
|
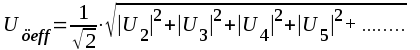 |
3. Omkopplaren ställes i läge II och potentiometern injuseras så (α varieras), att rörvoltmetern åter visar värdet UReff. Då gäller att
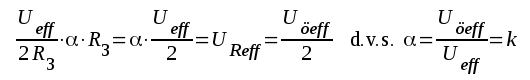 |
|
där 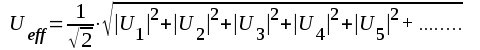 |
Potentiometern R3 kan alltså graderas i % klirrfaktor.
För att bryggan skall kunna undertrycka grundtonen skarpt utan att samtidigt dämpa övertonerna fordras, att den avstämbara bryggrenen har ett högt Q-värde, vilket kräver små r-värden. Den balanserade bryggan får därför en relaivt lågohmig ingång, vilket kan påverka mätobjektet.
link >