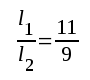< link link link >

    Låt oss utgå ifrån att vi känner eller har konstruerat den dynamiska j_a-v_g-kurvan för ett förstäkarsteg samt att  vi önskar bestämma eller åtminstone uppskatta utsignalens (j_a) distorsion (klirrfaktor, övertonsfaktor), då styrgallret matas av en sinussignal. Vi har exempelvis

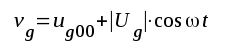där u_g00 = gallervilospänningen och U_g = gallersignalspänningens amplitud. v_g är alltså totala gallerspänningen.
    Med ledning av ovanstående kan vi nu konstruera utsignalens kurvform i analogi med fig. F2.41-42. Se härtill fig. F2.43, där i_a00 = anodströmmens vilovärde (anodströmmen utan signal).

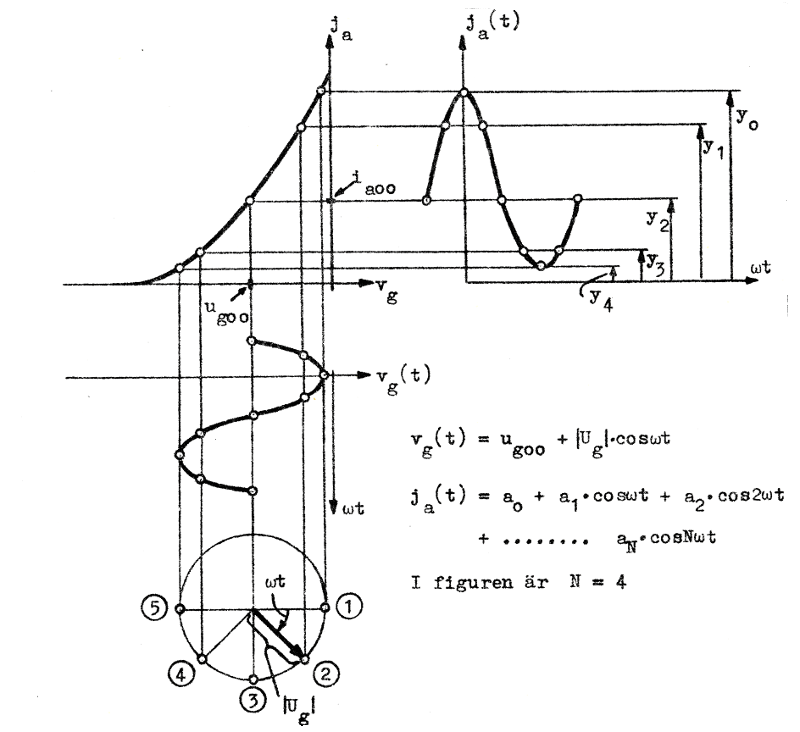Fig. F2.43. Grafisk distorsionsbestämning.

    Vi tillåter oss approximera utsignalen med en Fourier-serie med begränst antal termer (N+1 stycken):

F2.76

    Med vårt val av koordinatsystem blir utsignalen symmetrisk kring origo (ωt=0) och serien kommer därför endast att innehålla cosinustermer.
    Som av konstruktionen framgår har vi delat en halvperiod i N (N = 4 i fig. F2.43) lika långa tidsintervall (vinkelintervall) och vi får därvid N+1 delningspunkter (, , , , och  i fig. F2.43). Ur j_a-v_g-diagrammet kan vi nu avläsa N+1 värden på ja (y₀, y₁, y₂, y₃ och y₄ i fig. F2.43).
    Vi väljer nu seriens koefficienter (delsvängningarnas amplituder) a₀, a₁, a₂, a₃ och a₄ så, att seriens summa och den verkliga andoströmmens värde sammanfaller i delningspunkterna. Vi fär då ur sambandet F2.76 och fig. F2.43:

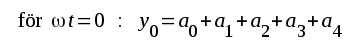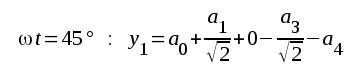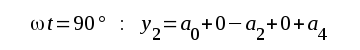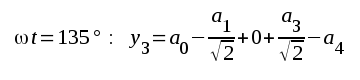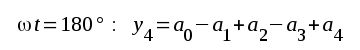    Ur detta ekvationssystem kan samtliga koefficienter a₀, a₁, a₂, ..... beräknas. Vi får:

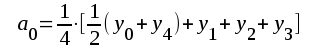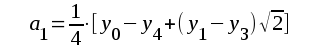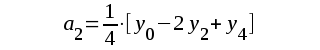	F2.77

    Serien F2.76, med koefficientvärden beräknade ur systemet F2.77, beskriver en kurva, som sammanfaller med verkliga j_a-kurvan i ett antal punkter men som mellan dessa kan få ett avvikande förlopp. Om , övergår en approximativa serien i en Fourier-serie.
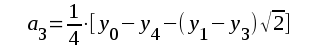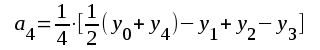    Antalet intervall N måste väljas åtminstone lika stor som den högsta grundtonsmultipel, man önskar beräkna.
    Med ledning av sambanden F2.77 kan vi nu uppskatta övertonsfaktorn d, klirrfaktorn k samt deltonsfaktorerna d₁, d₂, d₃ och d₄ (se sambanden F2.65-67, sid. F2.31). Vi får exempelvis

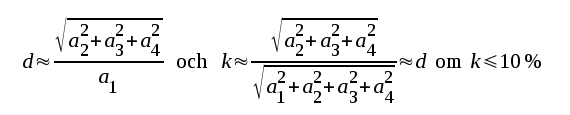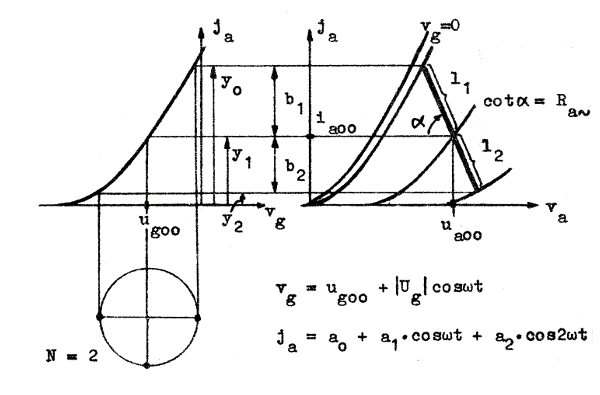
    Ibland (trioder, jämför fig. F2.41) nöjer man sig med två intervall (N = 2), d.v.s. j_a(t) beskrives med den starkt avkortade serien

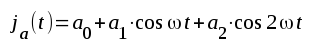    I analogi med räkningen på föregående sida kan läsaren visa, att vi nu får följande uttryck för seriens koefficienter (se även fig. F2.44).

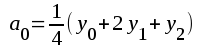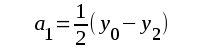	F2.78

    Deltonsfaktorn d₂ blir:

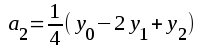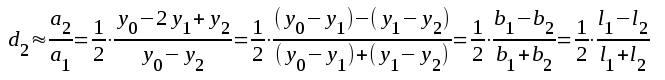F2.79

		Om vi tillåter, att deltonsfaktorn d2 fpår uppgå till 5%, erhåller vi ur sambandet F2.79:     Detta samband benämnes strundom "elva-nio-regeln".     Vi kan på ett relativt enkelt sätt bestämma erforderligt Ra~ för en maximal distorsion av c:a 5% genom attt vrida resistanslingen kring viopppunkten till dess kvoten l1/l2 = 11/9. Läsaren hänvisas till övningsexempel.
Fig. F2.44. Grafisk distorsionsbestämning och inpassning av resistanslinje för växelström.

link >