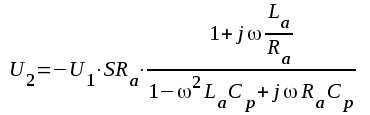Förstärkare av RC-kopplad typ användes i bl.a. radar- och TV-sammanhang. Dessa förstärkare (videoförstärkare) skall kunna förstärka mycket snabba tidsförlopp, t.ex. snabbt stigande och fallande, korta eller långa pulser. Med tanke på Fourier-analys vågar vi påstå, att vi av dylika förstärkare måste kräva stor bandbredd (låg undre gränsfrekvens och hög övre gränsfrekvens). Problement att utöka RC_stegets bandbredd såväl uppåt som nedåt är därför aktuellt. Hos ett förstärkarsteg begränsas bandbredden uppåt av parallellkapacitansen Cp, som därför genom lämligt val av rör och genom förståndig ledningsdragning måste pressas ned till ett minimum. Vid given Cp-storlek kan bandbredden ökas genom minskning av anodresistansen, vilket dock leder till minskad förstärkning. Samma resultat kan uppnås med motkoppling (se avsnitt F3). Vi kan emmellertid delvis kompensera parallellkapacitansens bandbreddsminskande verkan genom att utnyttja resonansen mellan parallellkapacitansen och en i kretsen inkopplad liten induktans. Vi kan därvid begagna oss av parallellresonans eller serieresonans. I förra fallet talar vi om shuntkompensering, i senare fallet om seriekompensering. I detta avsnitt skall vi något beröra det kompenserade RC-stegets förstäknings- och fasvridningsegenskaper. Videoförstärkarens återgivning av pulser och pulståg studerar vi i pulstekniken.
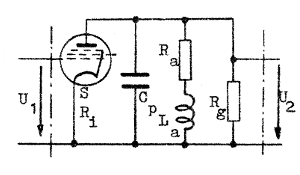 |
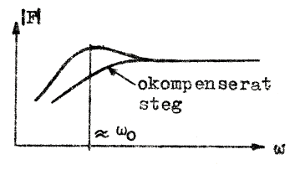
Shuntkompenseringens
princip framgår av signalschemat fig. F2.45. En
liten induktans La har lagts i serie
med anodresistansen Ra och vi får på
så sätt en starkt dämpad parallellresonanskrets,
vars impedans bör bli maximal i närheten av
resonansvinkelfrekvensen 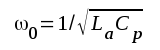 . Vi
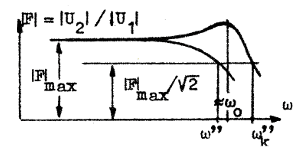
kan därför vänta oss en topp i
förstärkningskurvan i trakten av ω0
(fig. F2.46). Toppens höjd blir beroende av
kretsens Q-värde och dess läge på frekvensaxeln
bestämms av värdet på induktansen La.
Övre gränsvinkelfrekvensen ökar från värdet ω''
utan kompensering till värdet ω''k
med kompensering.
Av det sagda torde
framgå, att induktansvärdet La blir
litet och dess inverkan vid låg och medelhög
frekvens kan därför lämnas utan avseende. (Deta
gäller givetvis även RC-stegets kapacitanser Co,
Ck och C1 i det höga
frevensområde, som vi nu betraktar; jämför fig.
F2.1). . Vi
kan därför vänta oss en topp i
förstärkningskurvan i trakten av ω0
(fig. F2.46). Toppens höjd blir beroende av
kretsens Q-värde och dess läge på frekvensaxeln
bestämms av värdet på induktansen La.
Övre gränsvinkelfrekvensen ökar från värdet ω''
utan kompensering till värdet ω''k
med kompensering.
Av det sagda torde
framgå, att induktansvärdet La blir
litet och dess inverkan vid låg och medelhög
frekvens kan därför lämnas utan avseende. (Deta
gäller givetvis även RC-stegets kapacitanser Co,
Ck och C1 i det höga
frevensområde, som vi nu betraktar; jämför fig.
F2.1).
|
|
| Fig. F2.45. Signalschema för shuntkompenserat RC-steg. | ||
 |
||
| Fig. F2.46. Shuntkompenseringens inverkan. |
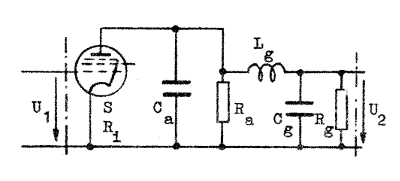
Vid studium av stegeeets egenskaper bör vi även ihågkomma, att kompenseringen är avsedd för mycket bredbandiga förstärkarsteg. Vi kan därför förutsätta, att anodreistansen Ra är relativt liten samt att röret är en pentod. Normalt är därför Ra<<Ri och Ra <<Rg, varför ekvivalenta småsignalschemat får en relativt enkel form (fig. F2.47). Vid beräkningar avseende detta schema bör vi observera, att Q-värdet är så lågt, att vi ej kan begagna oss av de kretsreduktioner, som vi använt vid resonanskretsarnas behandling.
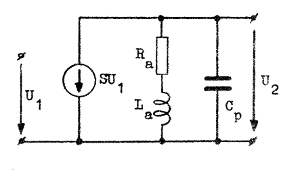
|
Ur schemat Fig. F2.47
erhålles:
|
|||
| Fig. F2.47. Ekvivalent småsignalschema under förutsättningen: Ra << Ri och Ra << Rg. |
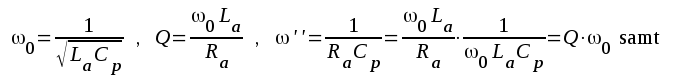 |
|
Införes dessa storheter i uttrycket för U2 ovan får vi:
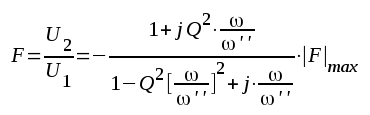 |
F2.80 |
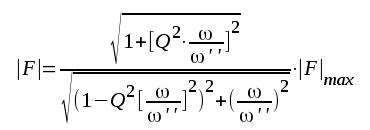 |
F2.81 |
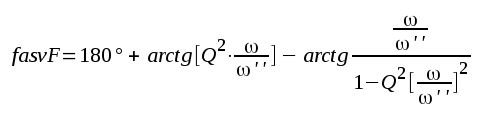 |
F2.82 |
I fig. F2.48 nedan har
 |
| Fig. F2.48. Kompenseringens inverkan på förstärkarstegets transmissionskurva. |
Beroende på vad man önskar uppnå med kompenseringen, kan Q-värdet väljas på olika sätt. Q = 0,64 ger sålunda s.k. maximalt flat kurva, medan Q = 0,56 ger maximalt linjär fasgång (jämför avsnitt F2.13). En jämförelse mellan fig. F2.48 och fig. B6.23 (sid. B6.26) kan vara av intresse i detta sammanhang.
|
Stegets uppbyggnad vid
serikompensering framgår av signalschemat fig.
F2.49. En liten induktans Lg (som inte har någon
inverkan vid låg eller medelhög frekvens) har
inlänkats mellan anodresistansen Ra
och gallerresistansen Rg. Lg-Cg
-systemet kan betraktas som en
sserieresonanskrets, varför vid
spänningsresonans spänningen över Cg
bör bil större än |
|
| Fig. F2.49. Signalschema för seriekompenserat RC-steg. |
spänningen över Ca. Vi kan därför även i detta fall vänta oss en topp i transimssionskurvan vid en frekvens, var storlek bsstämmes av den inlänkade induktansen Lg i kombination med kretsens fördelade kapacitanser. Om vi alltjämt förutsätter Ra << Ri får småsignalschemat vid hög frekvens ett utseende i enlighet med fig. F2.50 nedan.
 |
En beräkning av förstärkning
och fasvridning som funktion av frekvensen
är idetta fall mera komplicerad än i fall a)
ovan, vilket i första hand hänger samman med att
parallellkapacitansen Cp nu är
uppdelad i sina beståndsdelar Ca och
Cg. Vi nöjer oss här med att
konstatera, |
|
| Fig. F2.50. Ekvivalent småsignalschema, Ra << Ri. |
För den teoretiskt intresserade ges nedan uttrycket för den komplexa förstärkningen, beräknad med ledning av fig.F2.50.
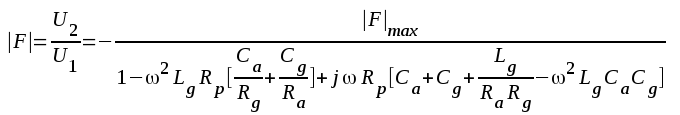 |
F2.83 |
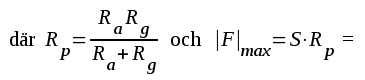 RC-stegets
förstärkning vid medelhög frekvens. RC-stegets
förstärkning vid medelhög frekvens. |
Med de ovan skisserade metoderna kan vi i viss utsträckning förbättra RC-stegets transmissionsegenskaper vid hög frekvens. I vissa fall kan det vara
 |
nog så viktigt att utsträcka stegets
transmissionsområde nedåt (sänka undre
gränsfrekvensen). Denna bestämmes av
kopplingskapacitansen Co (se
sambandet F2.14). Det ligger nära till hands att
utforma en kompensering vid låg frekvens på ettt
sätt, som påminner om metoden enligt b) ovan.
RC-stegets småsignalschema vid låg frekvens har
ett utseende enligt fig. F2.51 (inverkan av Ck
och C1 försummas; jämför fig. F2.1). |
|
| Fig. F2.51. Ekvivalent småsignalschema, Ra
<< Ri. |
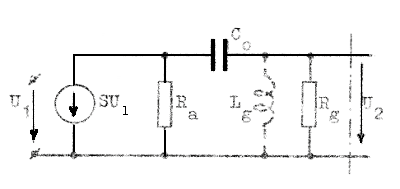
Om vi inkopplar en stor induktans i enlighet med fig. F2.51, kan vi vänta oss en topp i förstärkningskurvan i närheten av vinkelfrekvensen
 |
(fig. F2.52), vid vilken serieresonans
inträffar i C0Lg-grenen.
Metoden, som liknar b) ovan (låt Lg
och Cg i fig. F2.50 byta plats), är
dock knappast praktisk, efersom det erfoderliga
Lg-värdet blir mycket stort (spole med
järnkärna). |
|
| Fig. F2.52. Lågfrekvenskompenseringens inverkan. |
En annan kompenseringsmetod vid låg frekvens finnes redan inbyggd i vårt schema, fig. F2.1 (sid. F2.1). Om Ra >> Ri och om vi alltjämt försummar inverkan av katodkapacitansen Ck, får ekvivalenta småsignalschemat ett utseende enligt fig. F2.53 nedan.
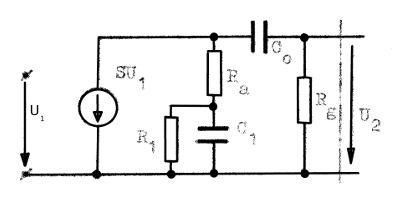 |
Om vi antar, att R1
>> 1/ωC1 erhålles
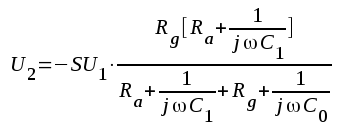 eller 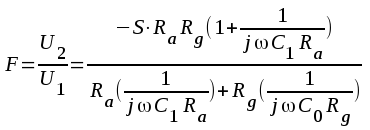 |
|
| Fig. F2.53. RC-stegets småsignalschema vid låg
frekvens (Ra>>Ri, 1/ωCk=0) |
Om vi i uttrycket för komplexa förstärkningen sätter RaC1 = RgC0, får vi
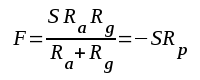 |
|
F är sålunda oberoende av frekvensen, viket hänger samman med det upenbara faktum, att strommen
I praktiken måste vi emmellertid välja ett ändligt värde på reistansen R1, varför vi vid extremt låg frekvens ej kan uppfylla villkoret R1>> 1/ωC1, som var en förutsättning för vår beräkning ovan. Vi kan dock med beskrivna metoden i någon mån kompensera för C0:s inverkan vid låg frekvens.
Som tidigare nämnts verkar avkopplingskapacitanserna Ck och Csg (fig. F2.31, sid. F2.26) förstärkningsminskande vid låg frekvens. Speciellt för katodavkoppling fordras mycket stora kapacitanser, varför man i bredbandsförstärkare ofta utelämnar katodkondensatorn och i stället godtar den förstärkningsminskning, som detta medför.
link >
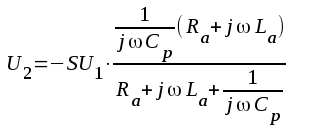 eller
eller