< link link link >

    Med återkoppling (engelska: feedback) menar vi, att ett sytems (t.ex. en förstärkares) utstorhet (utsignal) på något sätt återmatas till systemingången och adderas till eller subtraheras ifrån instorheten (insignalen). Adderas storheterna på systemingången talar vi om positiv återkoppling (positive feedback) eller medkoppling, subtraheras storheterna talar vi om negativ återkoppling (negative feedback) eller motkoppling.

Teorien för återkopplade system är av stor betydelse inom förstärkartekniken och av än större betydelse inom reglertekniken.

    Med hjälp av motkoppling kan man (på bekostnad av lägre förstärkning) minska en förstärkares distorsion, öka dess bandbredd och stabilitet samt ändra dess in- och utimpedanser. Medkoppling, som i förstärkare kan medföra instabilitet (självsvängning), är av speciell betydelse i oscillatorsammanhang.

    Låt oss studera en förstärkare med komplexa spänningsförstärkningen F. Förstärkarens utsignal U₂ påföres ett passivt nätverk (återkopplingsfyrpolen), var utsignal βU₂ återmatas till förstärkaringången och där subtraheras från insignalen U₁ i enlighet med fig. F3.1, som är prototypschemat för en återkopplad förstärkare. Den ursprungliga förstärkaren säges i motsats härtill vara en öppen förstärkare. β, som kan vara en komplex storhet, benämnes återkopplingskvoten och kan mera generellt sägas var återkopplingsfyrpolens överföringsfunktion. Fasvridningeni den ursprungliga förstärkaren (fasvF) och fasvridningen i återkopplingsfyrpolen (fasvβ) bestämmer tillsammans huruvida signalen βU₂ verkligen subtraheras ifrån eller adderas till insignalen U₁, d.v.s. är avgörande för om vi får positiv eller negativ återkoppling. Fig. F3.1 nedan har ritats så, att vi vid reella och positiva värden på β och F får motkoppling.

	Fig. F3.1. Den återkopplade förstärkarens principschema.

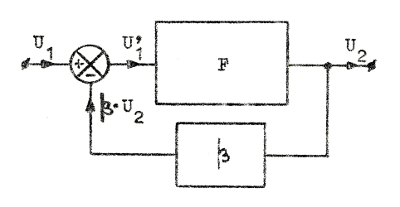
		Ett alternativt ritsätt är det enkla blockschemat enligt fig. F3.2, där pilarna markerar respektive storheters transportriktningar. Vidare har vi infört en speciell symbol, som anger, att två storheter skall subtraheras eller adderas (i det sistnämnda fall sättes + i de båda sektorerna).     Slutligen bör påpekas, att återkopplingsfyrpolen i ett generellt fall kan vara passiv eller aktiv.
Fig. F3.2. Det återkopplade systemets blockschema.

    Enligt fig. F3.2 får vi följande samband mellan systemets storheter:

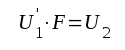	F3.1
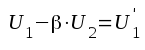	F3.2

    Eliminering av U'₁ ger det i teorin för återkopplade system grundläggande sambandet

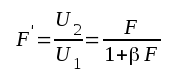F3.3

där F' är den återkopplade förstärkarens komplexa förstärkning.

    I fig. F3.1 har återkopplingsfyrpolen antagits vara en enkel resistiv spänningsdelare, varför vi har

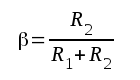  β är i detta fall positiv och reell. Om vi i denna inledande diskussion vidare antar, att F är en reell positiv konstant (den öppna förstärkaren har konstant förstärkning och ingen fasvridning), så framgår av sambandet F3.3 att motkopplingen minskar förstärkningen (1+βF) gånger.
Om βF>>1, blir

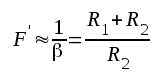d.v.s den motkopplade förstärkarens egenskaper bestämms i huvudsak av återkopplingsfyrpolen (i detta fall två resistanser). Vi kan därför vänta oss, att distorsion och störningar, som härrör från ursprungsförstärkaren, reduceras av motkopplingen. Förstärkarens egenskaper har med andra ord lineariserats genom motkopplingen.

link >