< link link link >

    För ett vanligt RC_kopplat förstärkarsteg har vi tidigare funnit (se sid. F2.7) att komplexa förstärkningen från medelhög frekvens och uppåt kan skrivas

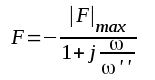F3.9

där ω'' är steget övre gränsfrekvens. Eftersom normalt undre gränsfrekvensen ω' << ω'' kan vi även säga, att ω'' är stegets bandbredd.     Om steget motkopplas får vi

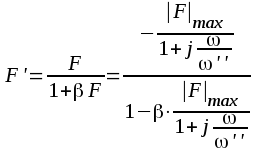F3.10

     Om β antages vara reell, måste vi i detta fall förutsätta ett negativt värde på β, om vi skall få motkoppling. Vi sätter därför -β=β₀, där β₀ är ett positivt reellt tal. Vi får då ur F3.10

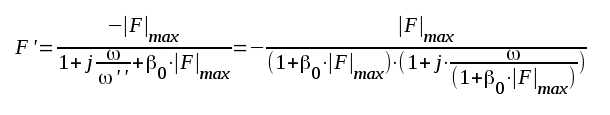eller kortare

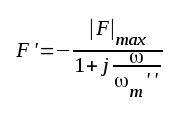F3.11

    Bandbredden har alltså ökat lika många gånger  som förstärkningen minskat, varav följer att försträkning-bandbredd-produkten är densamma före och efter motkoppling vid motkoppling av ett enkelsteg.

    För det öppna förstärkarsteget gäller enligt sambandet F3.9 att


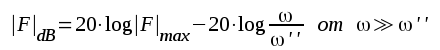och för det motkopplade förstärkarsteget gäller enligt sambandet F3.11 att

d.v.s. Bode-diagrammets asymptotiska beloppkurva faller vid höga frekvenser i båda fallen med 6 dB/oktav. Vidare visas lätt att f db = 0 och f = 0 för samma ω-värde (ω_c), vilket för vårt enkelsteg leder till den enkla konstruktionen i fig. F3.3 nedan.

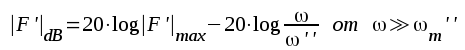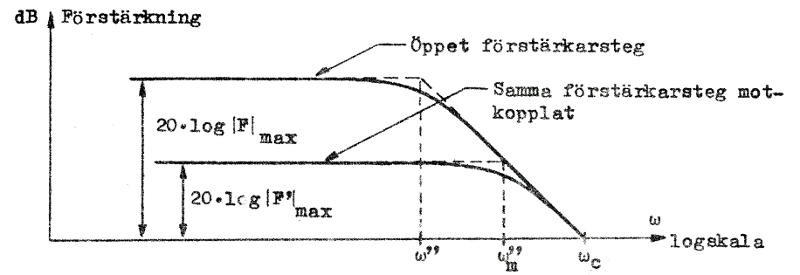Fig. F3.3. Motkopplingens inverkan på de RC-kopplade förstärkarstegets bandbredd.

    Det bör betonas, att fig. F3.3 avser ett specialfall, nämligen ett RC-kopplat förstärkarsteg. Vårt resultat är allmängiltigt i den bemärkelsen, att bandbredden ökar vid motkoppling, men det finnes ingen formel, som i ett generellt fall anger sambandet mellan bandbredden utan och bandbredden med motkoppling.

link >