 |
( se fig. F3.4; jämför detta schema
med småsignalschemat för en GK-kopplad triod med |
|
| Fig. F3.4 Ekvivalent schema för en förstärkare
med inimpedansen Zin , utimpedansen Zut och
tomgångsförstärkningen F0. |
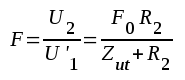 Fig. F3.12 Fig. F3.12 |
Den vid motkoppling till förstärkaringången återmatade spänningen kan vara proportionell mot förstärkarens utspänning (spänningsmotkoppling eller shutkoppling) eller mot förstärkarens utström (strömmotkoppling eller seriemotkoppling). Vi behandlar nedan dessa fall var för sig.
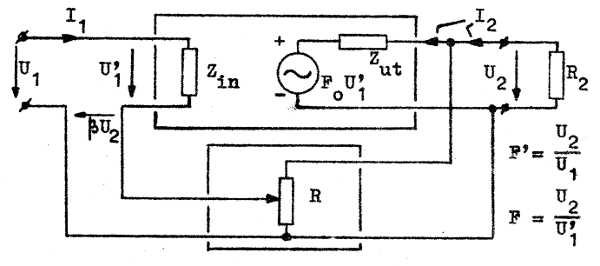 |
För enkelhets skull antages
motkopplingen ske via en enkel resistiv
spänningsdelare,varvid vi antar att R>>R2
(spänningsdelaren belastar ej
förstärkarutgången) Vidare antar vi, att |
|
| Fig. F3.5 Schema för beräkning av in- och
utimpedans. |
(spänningsdelningen β påverkas ej av Zin). Vi betecknar den motkopplade förstärkarens komplexa inimpedans med Z'in = U1 / I1. Vi får följande samband:
 |
|
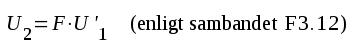 |
|
 |
|
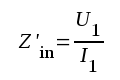 |
Eliminering av U2 i första ekvationen och därefter division med I1 ger direkt sambandet
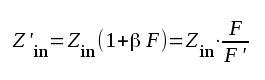 |
F3.13 |
Inimpedansen kommer alltså att öka i samma mån som förstärkningen avtar. Observera dock att uttrycket F3.13 härletts under vissa förutsättningar. Der är alltså ej ett generellt uttryck på den motkopplade förstärkarens inimpedans. Denna fär berkäknas i varje särskilt fall.
Läsaren visar nu lämpligen själv, att den motkopplade förstärkarens komplexa utimpedans blir
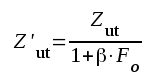 |
F3.14 |
Sambandet F3.14 har härletts under de förutsättningar, som ovan givits.
Spänningsmotkopplingen minskar allstå utimpedansen i ungefär samma proportion som förstärkningen avtar (
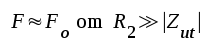 ).
). |
I detta fall återmatar vi
till ingången en spänning (U), som är
proportionell mot utströmmen (I2). Vi
antar för enkelhets skull, att R << R2
och att |
|
| Fig. F3.6 Schema för beräkning av in- och utimpedans. |
|
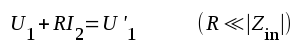
|
|
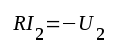 |
|
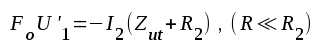 |
Eliminering av U'1 och I2 ger komplexa förstärkningen F':
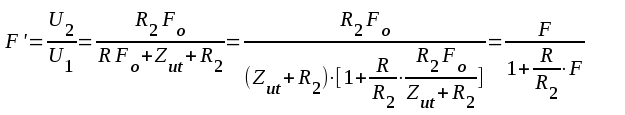 |
F3.15 |
där F är den öppna komplexa förstärkningen enligt sambandet F3.12.
Eliminierar vi i stället U2 och I2 ur ekvationssystemet ovan får vi:
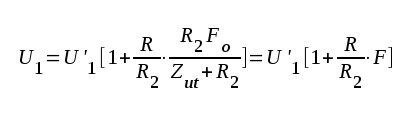 |
|
Divideras denna ekvation med I1 erhålles direkt
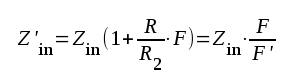 |
F3.16 |
där
Det överlämnas åt läsaren att visa, att den strömmotkopplade förstärkarens komplexa utimpedans blir
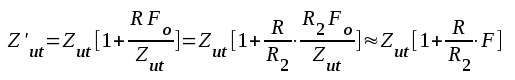 |
F3.17 |
där sista ledet erhålles, om
Utimpedansen ökar sålunda i ungefärlig proportion till förstärkningens avtagande.
link >