Införandet av motkoppling i ett system medför alltid viss risk föra instabilitet, d.v.s. självsväning. Om en förstärkare har frekvensoberoende egenskaper betyder motkoppling vid en frekvens också motkoppling vid alla andra frekvenser. Alla praktiska förstärkare har emellertid frekvensberoende egenskaper, vilket gör motkopplingsproblemet mera invecklat.
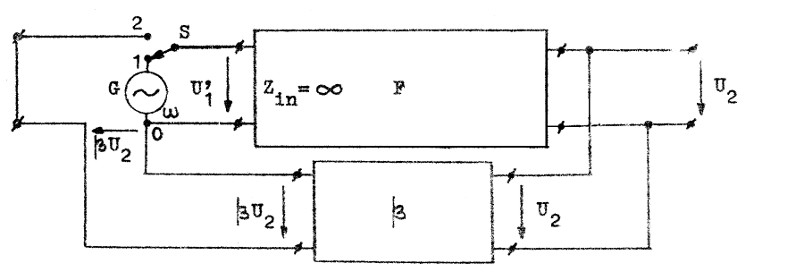
Låt oss genomföra ett tankeexperiment med systemet engligt fig. F3.21 där såväl F som
| |
 |
|
| |
Fig. F3.21. Schema, använt för
stabilitetsundersökning. |
|
Förstärkaren antages matad av sinusgeneratorn G , som ger spänningen U'1. Utsignalen från förstärkaren blir
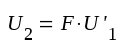 |
Antag nu att generatorfrekvensen w varieras från noll till oändligheten och att utspänningen från återkopplingsfyrpolen (
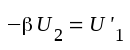 |
Om och när detta inträffar, föres omkopplaren S hastigt över från läge 1 till läge 2. Härigenom ändras ingenting i systemet och vi kan därför vänta oss, att systemet fortsätter att arbeta, trots att signalkällan G bortkopplats. Systemet kan väntas självsvänga.
Enligt vårt resonemang fordras för självsvängning att vid någon frekvens villkoret
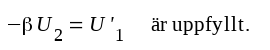 |
Eftersom
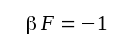 |
F3.35 |
Villkoret F3.35 kan vi även uttrycka med det s.k. amplitudbalansvillkoret och fasbalansvillkoret:
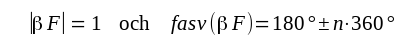 |
F3.36 |
där n = 0, 1, 2, 3........
Om man vid experiment ovan vid någon frekvens funnit, att amplituden på spänningen mellan 2 och 0 därvid haft samma fasläge som xx och att spänningen mellan 2 och 0 därvid haft samma fasläge som U'1, visar ett liknande resonemang, att man får självsvängning med växande amplitud vid omkopplarens omläggning från läge 1 till läge 2 (se härtill avsnitt H1.01).
Villkoret för självsvängning kan därför formuleras på följande sätt
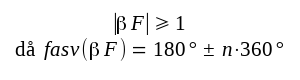 |
F3.37 |
som benämnes Barkhausens sjävsvängningskriterium.
I belysning av vårt svängningskriterium kan vi säga, att självsvängningen uppkommer på grund av att återkopplingen vid en viss frekvens blir positiv och vid samma frekvens har stor styrka.
Vår motkopplade förstärkare får emellertid ej självsvänga. Villkoret härför blir:
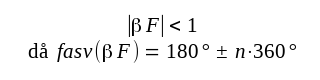 |
F3.38 |
där n = 0, 1, 2, 3........
Med denna formulering benämnes sambandet F3.38 Barkhausens stabilitetskriterium, som är ett tillräckligt men i vissa fall ej nödvändigt villkor för stabilitet i en återkopplad förstärkare.
Om vi i komplexa talplanet ritar den kurva, som komplexa slingförstärkningsvisarens spets beskriver, då
Antag att detta diagram för fem olika motkopplade förstärkare har utseendet enligt kurva
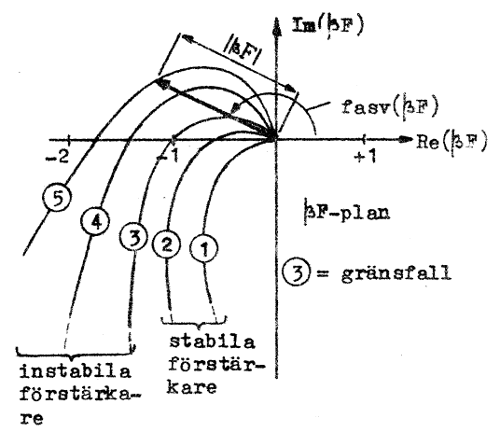 |
enligt kriteriet F3.38
stabila förstärkare. För kurva Barkhausens stabilitetskriterium innebär alltså, att slingförstärkningens Nyquist-diagram ej får skära negativa realaxeln i eller till vänster om punkten -1+j0. |
|
| Fig. F3.22. Komplexa slingförstärkningens
Nyquist-diagram för fem olika motkoppklade
förstärkare. |
Det kan nu vara lämpligt att diskutera ett praktiskt exempel. En typisk 3-stegs RC-kopplad förstärkare med identiskt lika steg antages ha ett signalschema enligt fig. F3.23. Förstärkaren motkopplas enligt figuren och vi frågar oss, vilket är det största värde på resistansen R, som kan tillåtas, utan risk för självsvängning?
För förstärkaren antages följande data gälla:
 |
Vi inför
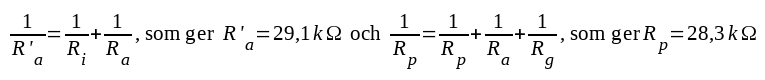 |
R utgör, som framgår av figuren, en del av resistansen Rg.
| |
 |
|
| |
Fig. F3.23. 3-stegs RC-kopplad förstärkare. |
|
Med figurens riktningsbeteckningar blir
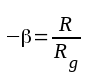 |
F3.39 |
Den motkopplade förstärkarens komplexa förstärkning blir enligt sambandet F3.3
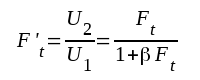 |
F3.40 |
där
Vid medelhög frekvens är
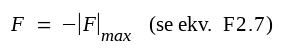 |
F3.41 |
där
Vid låg frekvens gäller för ett steg
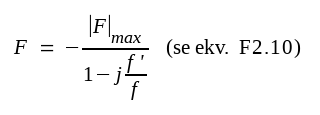 |
F3.42 |
där
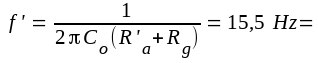 det enskilda stegets undre
gränsfrekvens (se ekv. F2.13).
det enskilda stegets undre
gränsfrekvens (se ekv. F2.13).Vid hög frekvens gäller för ett steg
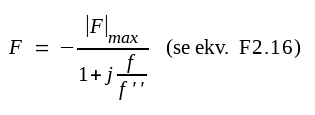 |
F3.43 |
där
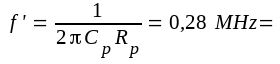 det enskilda stegets övre
gränsfrekvens (se ekv. F2.15).
det enskilda stegets övre
gränsfrekvens (se ekv. F2.15).Komplexa slingförstärkningen vid låg frekvens erhålles ur sambanden F3.39 och F3.42:
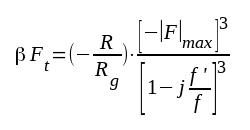 |
F3.44 |
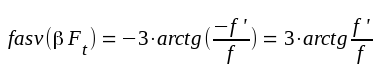 |
F3.45 |
Vid en viss låg frekvens f1 blir
 |
|
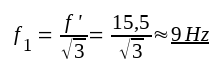 |
F3.46 |
Komplexa slingförstärkningen vi hög frekvens erhålles ur sambanden F3.39 och F3.43:
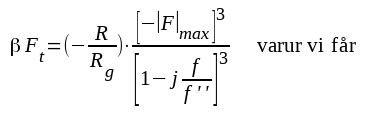 |
F3.47 |
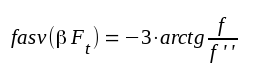 |
F3.48 |
Vid en viss hög frekvens f2 blir
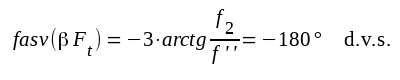 |
|
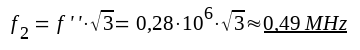 |
F3.49 |
Enligt ovan finns det alltså två frekvenser
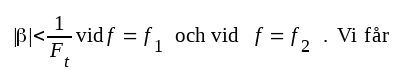 |
|
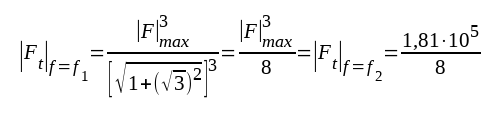 |
Alltså skall
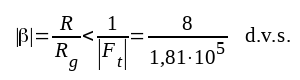 |
|
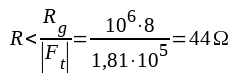 |
F3.50 |
R måste alltså väljas mindre än 44 ohm, om den motkopplade förstärkaren skall vara stabil.
Med det beräknade kritiska värdet på
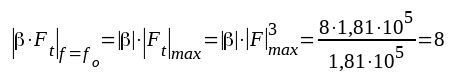 |
Slingförstärkningen måste sålunda vid medelhög frekvens understiga värdet 8, ty i annat fall blir
I fig. F3.24 nedan har Nyquist-diagrammet för komplexa slingförstärkningen
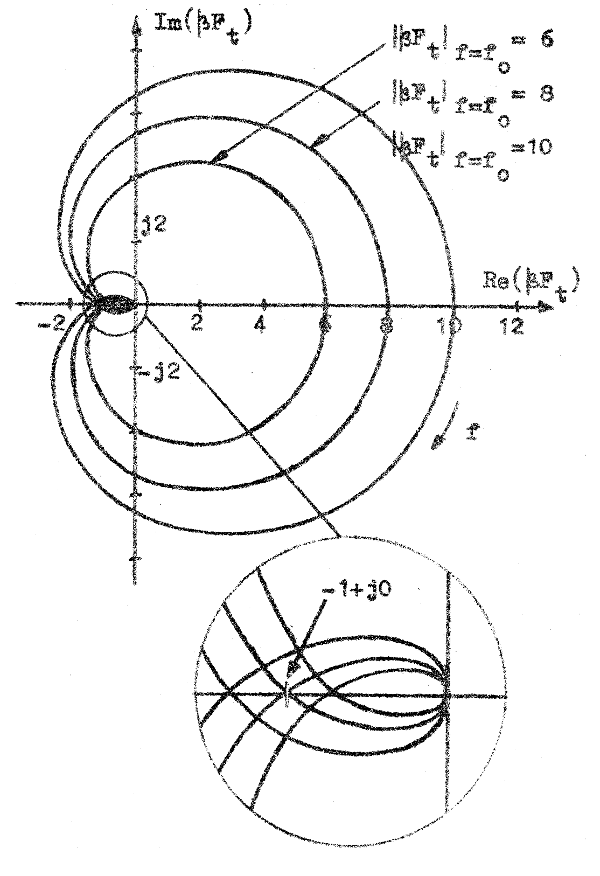 |
Jämför vi med diskussionen
på sid. F3.20 innebär de båda sistnämnda
värdena, att förstärkaren är instabil, medan
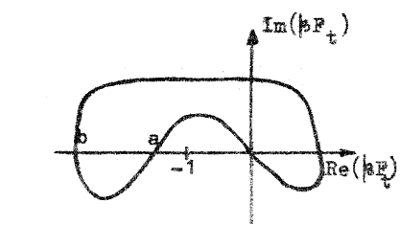
värdet 6 innebär en stabil förstärkare. Det kan tänkas inträffa, att slingförstärkningens Nyquist diagram för en viss förstärkare får det i fig. F3.25 skisserade utseendet. Mellan punkterna a och b på negativa realaxeln är Observera i detta sammanhang påpekandet på sid. F3.19, att Barkhausenvillkoret F3.38 är ett tillräckligt men ej nödvändigt villkor för stabilitet. |
|
| Fig. F3.24. Komplexa slingförstärkningens
Nyquist-diagram i en 3-stegs RC-kopplad
förstärkare. |
Enligt Nyquist är en förstärkare stabil, om slingförstärkningskurvan i Nyquist-diagrammet ej innesluter punkten -1+j0. Detta nämnt som en orientering.
 |
Ett närmare studium av hithörande frågor sker
inom reglertekniken. I detta sammanhang bör nämnas, att information angående en förstärares stabilitet även kan erhållas genom studiumav slingförstärkningens Bode-diagram. Studerar vi alljämt vår 3-stegsförstärkare, så har vi enligt sambandet F3.47 vid hög frekvens: |
|
| Fig. F3.25. Exempel på Nyquist-diagram för en
villkorligt stabil förstärkare. |
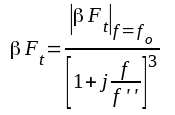 |
F3.51 |
Vi uttrycker slingförstärkningen
 |
F3.52 |
där f'' = 0,28 MHz enligt tidigare beräkning.
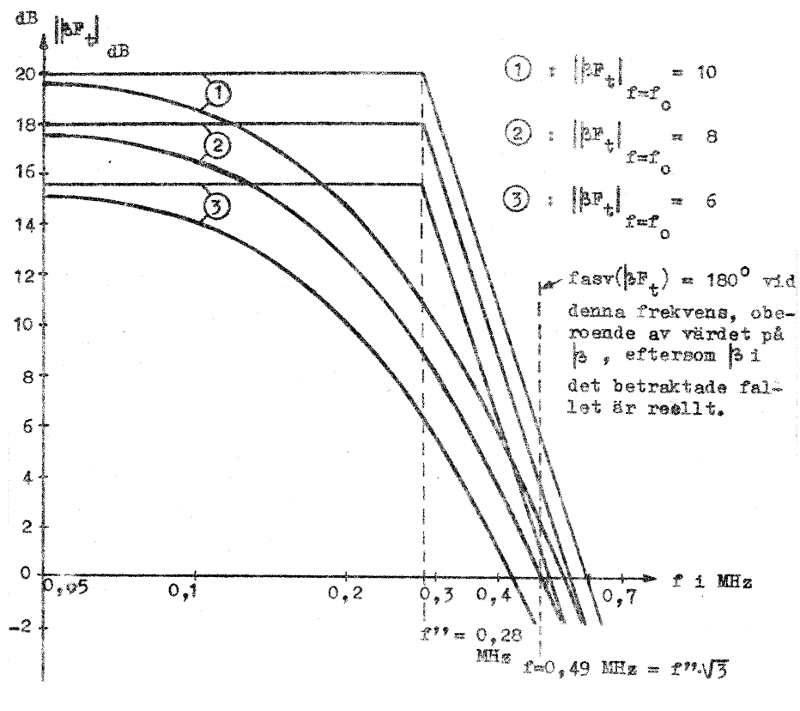
I fig. F3.26 nedan har med ledning av sambandet F3.52 slingförstärkningens asymptotiska och verkliga beloppkurva ritats för några olika värden på slingförstärkningen vid medelhög frekvens (några olika värden på
Vidare har i diagrammet den frekvens, vid vilken
| |
 |
|
| |
Fig. F3.26. Slingförstäkningen vid hög frekvens,
presenterad i ett Bode-diagram, där såväl
asymptotiska som verkliga beloppkurvor utritats. |
|
Studerar vi diagrammets verkliga beloppkurvor finner vi för kurva
Kurva
Hade vi bedömt förstärkaren enbart med ledning av de asymptotiska kurvorna, hade vi eventuellt befarat instabilitet i samtliga tre fall, eftersom all asymptotkurvorna har ett dB-tal, som är större än noll vid f = 0,49 MHz. Hade vi å andra sidan dimensionerat förstärkaren så att de asymptotiska beloppkurvorna passerat under 0-dB-punkten vid f = 0,49 MHz, så hade förstärkaren med god marginal varit stabil.
Ett resonemang av den typ vi ovan fört kan givetvis genomföras även vid låg frekvens.
Kurvorna i fig. F3.26 ger oss en tankeställare: om kurvorna i trakten av transmissionsområdets gräns fallit snabbare (brantare) med frekvensen, så skulle nivån vid medelhög frekvens kunnat höjas (motkopplingsgraden ökas) utan risk för självsvängning
Det vore sålunda fördelaktigt om de kretsar, som utgör kopplingen mellan stegen i vår 3-stegsförstärkare, eller om återkopplingsfyrpolen kunde utformas så, att amplituden
link >