< link link link >

     Bestämning av rörets vilopunkt och bestämning av rörparametrarna i vilopunkten har behandlats i ett flertal sammanhang och förbigås därför här.
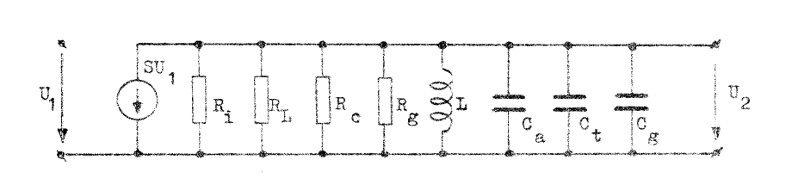
     Eftersom steget arbetar vid radiofrekvens, kan vi alltid välja kapacitanserna C_k, C_sg, C₁ och C₀ så stora, att de utan vidare kan betraktas som kortslutningar. Vidare är resonanskretsens förluster (representerade av r_L och r_c ; r_L >> r_c i normala fall) vanligen så små, att reduktionsreglerna i avsnitt A5 (sid. A5.1) kan tillämpas. Med hänsyn till vad ovan sagts får stegets ekvivalenta småsignalschema nedanstående form (fig. F4.4).

	Fig. F4.4. Ekvivalent småsignalschema för det enkelavstämda RF-steget i fig. F4.3.

     Vi inför beteckningen C för stegets totala parallellkapacitans och får

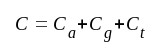F4.1

     Vi inför vidare resonansvinkelfrekvensen ω₀, som är

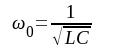F4.2

     I fig. F4.4 har vi redan med utnyttjande av de ovan nämnda reduktionsreglerna infört beteckningarna

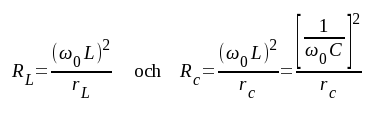F4.3

     Slutligen inför vi beteckningen R för den resulterande parallellresistansen:

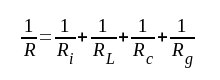F4.4

     Med de ovan införda storheterna får småsignalschemat nu den enkla form, som visas i fig. F4.5 nedan. Vid resonans upphäver L och C varandras

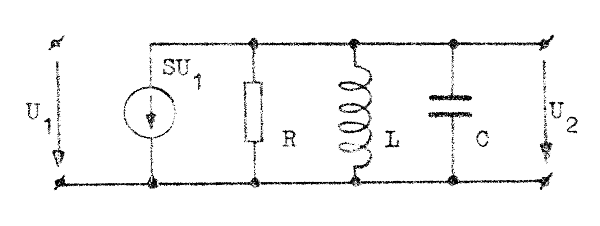		verkan och schemat får då samma form som RC-stegets småsignalschema vid medelhög frekvens. Med hänvisning härtill kan vi direkt säga, att stegets förstärkning vid resonans blir lika med
Fig. F4.5. Det enkelavstämda RF-stegets småsignalschema.

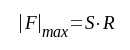F4.5

     Med tanke på vår tidigare, utförliga behandling av resonanskretsarna (se speciellt avsnitt B2.02, sid. B2.3, men även avsnitt B1.04, sid. B1.6) torde läsaren med lätthet verifiera riktigheten av nedanstående sammanfattande uttryck för det enkelavstämda stegets egenskaper.

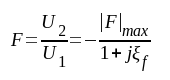	F4.6
	F4.7
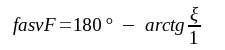	F4.8

     Om drift-Q-värdet Q > c:a 10, kan vi, som tidigare visats (sid. B1.7), inom resonansområdet med god noggrannhet sätta

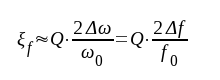F4.9

    

    Vid gränsfrekvenserna och bandbredden blir (jämför sid. B1.7):

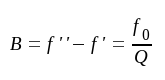F4.10

    Mellan resonansfrekvensen f0 och gränsfrekvenserna f' och f'' råder som bekant (sid. B1.7) sambandet

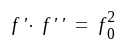F4.11

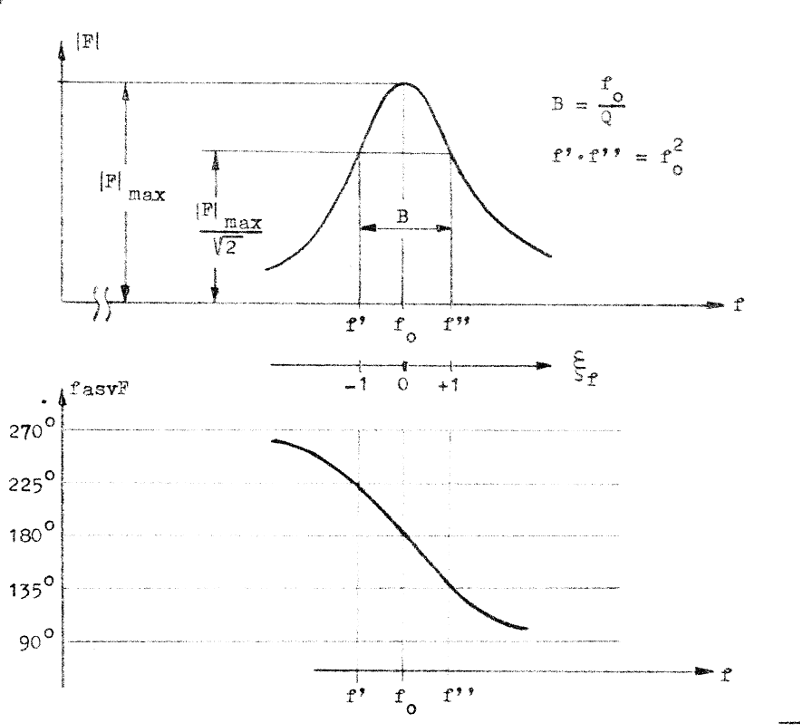
    Stegets transmissionskurvor, av vilka amplitudkurvan är en typisk resonanskurva, framgår av fig. F4.6 nedan.

	Fig. F4.6. Det enkelavstämda stegets transmissionskurvor.

    Vid dimensionering av steg av ovan behandlad typ är normalt f₀, B och  givna storheter. Sambandet F4.10 bestämmer då erforderligt drift-Q-värde. Efter val av lämpligt rör kan vi beräkna erforderligt induktansvärde L ur sambandet F4.5, som vi skriver


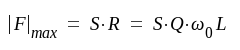varefter sambandet F4.2 ger erforderligt C-värde (C_t-värde).

    Alternativt kan vi vid dimensionering förutsätta, att f₀ och B är givna men att vi önskar göra så stor som möjligt. I så fall skriver vi


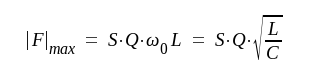    Stort värde på kräver ett litet värde på C, som emellertid ej kan göras mindre än C_a+C_g. De ofrånkomliga rör- och strökapacitanserna bestämmer alltså hur stor förstärkningen vid resonans kan göras. Speciellt om Q-värdet är högt är det mindre lämpligt att låta C_a+C_g utgöra kretsens enda kapacitanser, eftersom olika vilopunkter eller byte av rör ger varierande värden på C_a och C_g. Särskilt allvarligt är detta, om det efterföljande steget är utrustat med manuell eller automatisk förstärkningsreglering, eftersom C_g kan variera med det efterföljande stegets förstärkning (Miller-effekten).

link >