< link link link >

    Kaskadkopplar vi n enkelavstämda steg, vart och ett avstämt till frekvensen f₀, talar vi om synkron avstämning i motsats till spridd avstämning, även kallad sicksack-avstämning (engelska: stagger tuning). I senare fallet kan de olika stegen vara avstämda till olika frekvenser, som på visst sätt grupperar sig kring "kanalmittfrekvensen" f₀.

    a) Synkront avstämda steg.

    Om vi kaskadkopplar n lika steg, vart och ett med komplexa förstärkningen F (enligt sambandet F4.6), så blir den totala komplexa förstärkningen

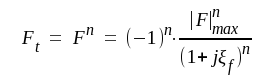F4.14

    Vidare blir

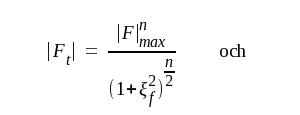F4.15

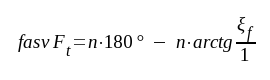F4.16

    För beräkning av n-stegsförstärkarens bandbredd sätter vi med ledning av sambandet F4.15

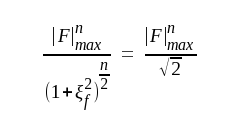F4.17

som ger

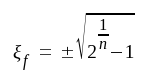F4.18

    Av sambanden F4.18 och F4.9 följer direkt att

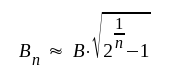F4.19

där B_n = n-stegsförstärkarens bandbredd och där B = det enskilda stegets bandbredd.

    Jämför sambandet F4.19 med sambandet F2.53 ( sid. F2.22).

    Om n > c:a 3 kan sambandet F4.19 med god noggrannhet approximeras med uttrycket

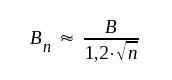F4.20

    Det kan vara av intresse att ställa sig frågan: hur många steg erfordras, om vi föreskriver en viss rörtyp och en viss total bandbredd (givna värden på S, C_a, C_g och B_n) samtidigt som vi föreskriver, att totalförstärkningen skall vara så stor som möjligt?

    Enligt sambandet F4.20 erfordras för det enskilda steget bandbredden


    Det enskilda steget skall alltså ha drift-Q-värdet


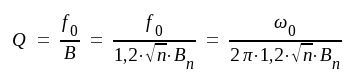    Den erforderliga parallellresistansen blir


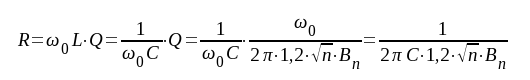    Resonansförstärkningen per steg blir


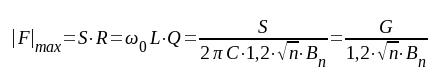där sista ledet följer av sambandet F4.13. För att få stor resonansförstärkning har vi gjort C_t = 0, d.v.s. C = C_a + C_g.

    Totalförstärkningen vid resonans blir


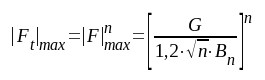    Vi söker nu maximum för , då n varierar. Läsaren verifierar, att vi får:

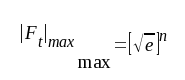F4.21

    som inträffar för det optimala n-värdet

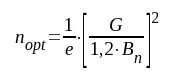F4.22

    Vid föreskriven total bandbredd B_n lönar det sig alltså ej att kaskadkoppla flera än ett begränsat antal synkront avstämda RF-steg.

Övning:  Rita  som funktion av n för G/B_n = 5, 6 och 7.

    Det kan i detta sammanhang även vara av intresse att undersöka hur mycket en störande signal på frekvensen fs dämpas relativt en signal på frekvensen f₀ (kanalmitten).

    I en n-stegsförstärkare av ovan beskriven typ förstärkes f₀-signalen


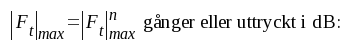    gånger eller uttryckt i dB:

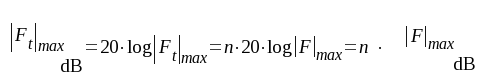F4.23

där 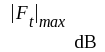 = hela förstärkarens resonansförstärkning i dB och där 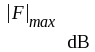 = det enskilda stegets resonansförstärkning i dB.

    f_s-signalen förstärkes (enligt sambandet F4.15) följande antal gånger


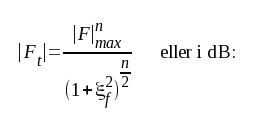    eller i dB:

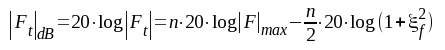F4.24

    I sambandet F4.24 är

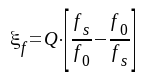
    Störsignalen f_s råkar alltså ut för en dämpning A dB relativt en signal på frekvensen f₀. Här är enligt sambanden F4.23 och F4.24:


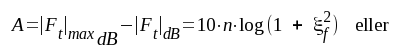    eller

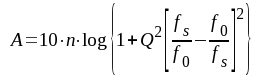F4.25

    Om f_s ligger långt över eller under f₀, blir  │ξ_f│ >> 1 och uttrycket för A kan då något förenklas. Sambandet F4.25 förutsätter, att Q-värdet är någorlunda konstant inom det betraktade frekvensområdet.

    b) Sicksack-avstämda steg.

    Önskar vi en transmissionskurva av mera flat typ (se t.ex. fig. F4.2) ligger det nära till hands att avstämma de olika stegen i en flerstegsförstärkare till olika frekvenser (sicksack-avstämning, "stagger tuning"I. I princip kan vi ha ett godtyckligt antal till olika frekvenser avstämda steg i kaskad, men av olika skäl användes normalt två ("stagger pairs") eller tre ("staggered triples") steg. Dylika grupper om två eller tre kaskadkopplade steg kan i sin tur kaskadkopplas.

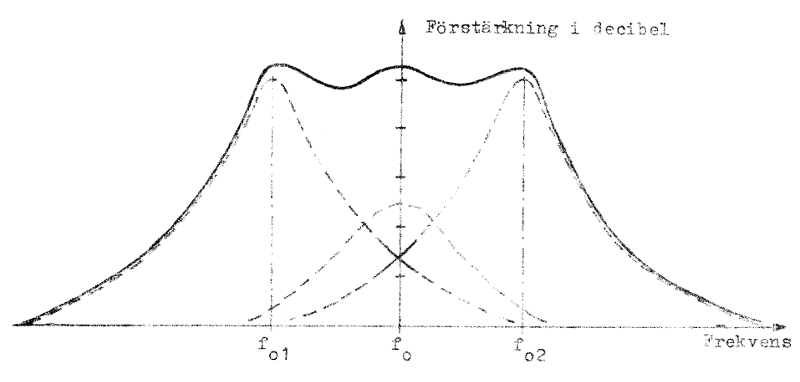
    Totalförstärkningen är produkten av de enskilda stegens förstärkningar (eller summan av deras förstärkningar uttryckt i dB). I fig. F4.7 har frekvenskurvorna (förstärkningen uttryckt i dB) för tre till olika frekvenser (f₀₁, f₀ och f₀₂) avstämda steg ritats (streckade kurvor). Den heldragna kurvan är totalförstärkningen, då de tre stegen kaskadkopplas.

	Fig. F4.7. Exempel på resulterande transmissionskurva (heldragen), då tre sicksack-avstämda steg kaskadkopplas (avstämningsfrekvenser f01, f0 och f02).

    Låt oss något mera detaljerat studera det enklaste fallet: 2 sicksack-avstämda, kaskodkopplade steg, av vilka de ena är avstämt till frekvensen f₀₁ och det andra till frekvensen f₀₂ (f₀₂ > f₀₁). I övrigt antar vi, att stegen är lika, d.v.s. de har lika stora förstärkningar och bandbredder. För de två stegen gäller enligt sambandet F4.7:


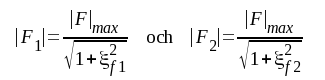där │F│_max är maximalförstärkningen (resonansförstärkningen) i vartdera steget. Vi förutsätter, att approximationen F4.9 kan tillåtas och får:


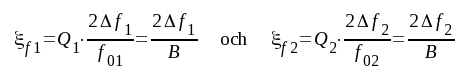    Sista ledet i ovanstående båda uttryck följer av sambandet F4.10 samt förutsättningen ovan: samma bandbredd B i de båda stegen.

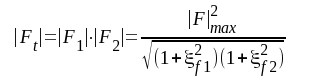F4.26

    Vi inför storheten f₀ (mittfrekvensen) genom definitionen:

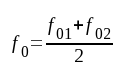F4.27

    Approximativt gäller att

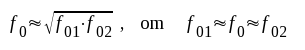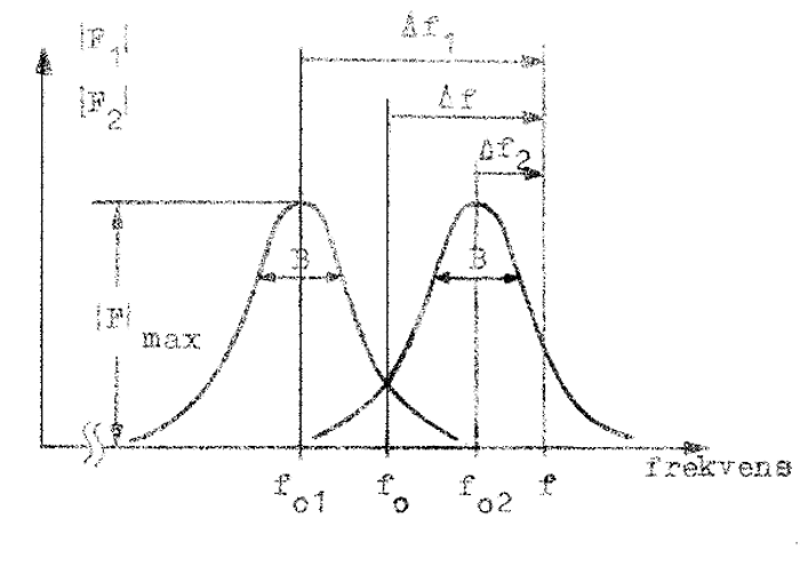		En godtycklig frekvens f anger vi genom storheten Δf = f -f0, som får var vår frekvensvariabel i stället för Δf1 och Δf2 (se fig. F4.8). Med ledning av nämnda fig. erhålles: Δf1 = Δf + f0 - f01 och Δf2 = Δf - (f02 - f0) varur vi får
Fig. F4.8. Definition av storheter i 2-stegsfallet.

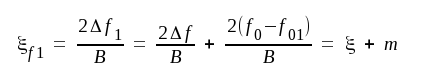	F4.28
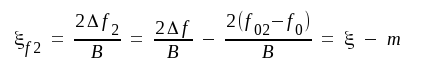	F4.29
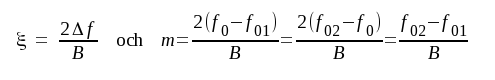	F4.30

    Eftersom m ⋅ B = f₀₂ - f₀₁ enligt sambandet F4.30, så anger tydligen storheten m frekvensavståndet mellan de båda stegens resonansfrekvenser, uttryckt i "antal bandbredder" (B för det enskilda steget).

    Med ledning av sambanden F4.26, F4.28 och F4.29 kan totalförstärkningen nu skrivas under formen

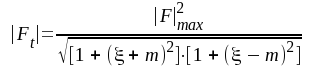F4.31

     ξ,  som är direkt proportionell mot Δf, får i fortsättningen vara vår normerande frekvensvariabel.

		I sambandet F4.31 kan vi ge m olika värden (ändra frekvensavståndet mellan stegens resonansfrekvenser). För varje m-värde får vi olika │Ft│- kurvor, t.ex. i enlighet med fig. F4.9. Av denna figur att döma bör vi kunna finna ett värde på m, som gör │Ft│- kurvan någorlunda plan på toppen. Låt oss därför i första hand undersöka │Ft│- kurvans maxima och minima.
Fig. F4.9. Sambandet F4.31.

    Det är därvid tillfyllest att undersöka uttrycket


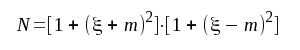ty då N = maximum är │F_t│ = minimum och vice versa.

    Vi bildar ekvationen


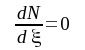    Läsaren visar på egen hand att denna ekvation får formen

F4.32

    Ekvationen har rötterna

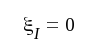	F4.33a
	F4.33b
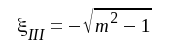	F4.33c

     De båda rötterna ξ_II och ξ_III är till beloppet lika stora men de har olika tecken, och ligger därför symmetriskt kring roten ξ_I, som motsvarar det maximum eller minimum, vilket på grund av symmetrien alltid inträffar för ξ = 0. Endast om m > 1 får ekvationen tre reella rötter, innebärande två maxima (toppar) och ett däremellan liggande minimum (dal). Om m < 1 har ekvationen endast en reell rot och frekvenskurvan är enkeltoppig. Är slutligen m = 1, har ekvationen en trippelrot för ξ = 0 och frekvenskurvan blir då "maximalt flat". Detta fall visas i fig. F4.10 nedan. m = 1 innebär, att frekvensavståndet mellan de båda stegens resonansfrekvenser är B, där B är det enskilda stegets bandbredd.

    Om m = 1, får förstärkningsuttrycket F4.31 den enkla formen

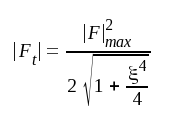F4.34

    Läsaren visar själv, att tvåstegsförstärkarens fasvridning i fallet m = 1 blir

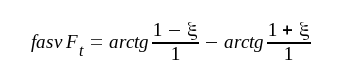F4.35

    Den mot F4.35 svarande faskurvan har ritats i fig. F4.10.

    Slutligen har i fig. F4.10 transmissionskurvan även ritats för det fall, att man kaskadkopplar två lika förstärkare, varvid varje förstärkare antages bestå av två sicksackavstämda steg av den typ, som ovan behandlats. Förstärkningen erhålles i detta fall som kvadraten på │F_t│ (sambandet F4.34).

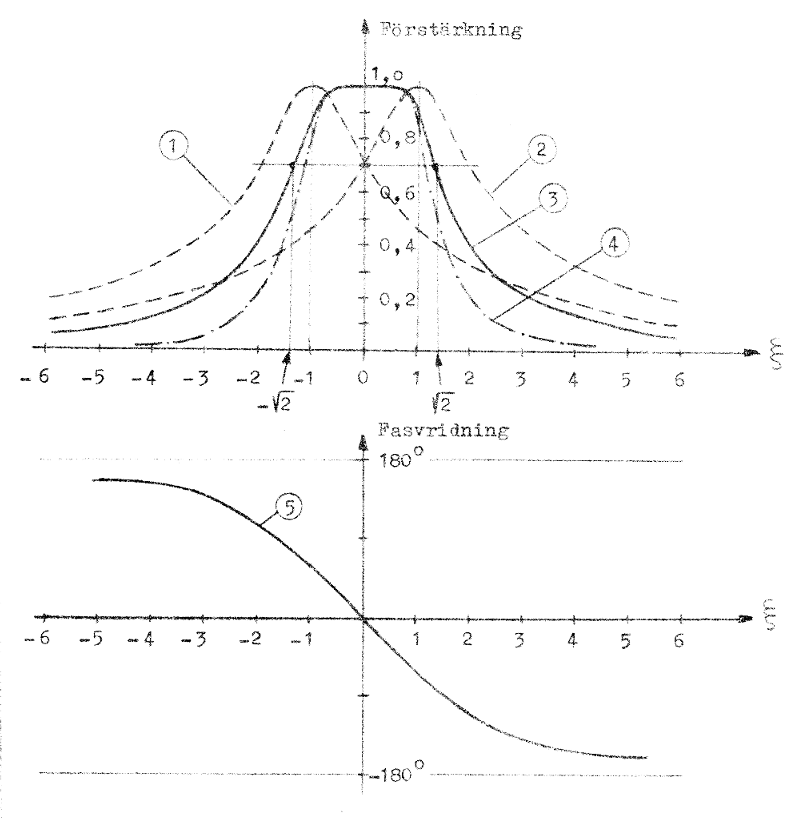
	Fig. F4.10. Transmissionskurvor och faskurva. Samtliga transmissionskurvor är normerade med avseende på maximalförstärkningen.

1. Frekvenskurva för det ena av de båda stegen.
2. Frekvenskurva för det andra av de båda stegen.
3. Frekvenskurva för den sicksack-avstämda tvåstegsförstärkaren.
4. Frekvenskurva för en förstärkare bestående av två kaskadkopplade förstärkare, var och en med en frekvenskurva enligt kurva 3.
5. Faskurva (fasvF_t) hörande till beloppkurva 3.
   

    Av sambandet F4.34 framgår direkt, att förstärkningen nedgått till 1/√2 av maximalförstärkningen, då ξ = ±√2. Enligt uttrycket för storheten ξ (sambandet F4.30) blir 2-stegsförstärkarens bandbredd B₂:

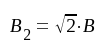F4.36

där B = de enskilda stegens bandbredd.

    Vid dimensionering av tvåstegsförstärkare av ovan beskrivna typ är givetvis i första hand B₂ och f₀ att betrakta som givna storheter. B kan då bestämmas ur sambandet F4.36, varefter de enskilda stegen kan dimensioneras på i princip samma sätt som de synkront avstämda stegen. Vi måste dock ihågkomma, att räkningarna ovan förutsätter, att approximationen F4.9 kan tillåtas. Detta är ej fallet om den erforderliga bandbredden B₂ är relativt stor (t.ex. B₂ = 8 MHz vid f₀ = 10 MHz). En noggrannare beräkning måste då genomföras.

    Läsaren inbjudes att på egen hand genomföra en undersökning av en trestegs sicksackavstämd förstärkare, där det tredje steget avstämmes till bandmitten.

    De fördelar, vi uppnått med sicksack-avstämmning jämförd med synkron avstämning, är framför allt, att förstärkningen blir mera jämn inom en stor del av det egentliga transmissionsområdet samt att förstärkningen faller snabbare utanför detta område.

link >