< link link link >

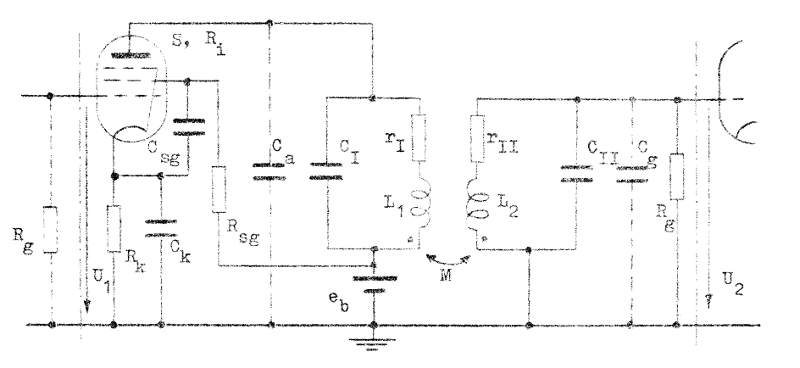
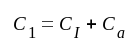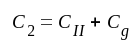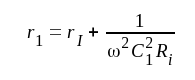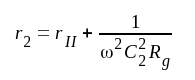I s.k. MF-förstärkare (MF= mellanfrekvens) i exempelvis radiomottagare (för såväl AM som FM) men även i andra sammanhang användes ofta induktivt kopplade kretsar (bandfilter, MF-transformatorer) mellan stegen. Även kapacitivt kopplade kretsar förekommer, men vi inskränker oss här till en orientering om det induktivt kopplade, dubbelavstämda steget med schema enligt fig. F4.11 nedan. Med ett dylikt steg kan vi få en transmissionskurva av i princip samma typ, som vi tidigare erhållit med den sicksackavstämda tvåstegsförstärkaren.


	Fig. F4.11. Dubbelavstämt radiofrekvens-förstärkarsteg.

I fig. F4.11 gäller beträffande R_k, R_sg, R_g, C_k och C_sg vad som tidigare sagts om det enkelavstämda steget (sid. F4.2). Avstämning av parallellresonanskretsarna kan ske med C_I och C_II eller med L₁ och L₂. C_a och C_g utgör oundvikliga rör- och ledningskapacitanser (inklusive Millereffekten), medan r_I och r_II representerar själva svängningskretsarnas förluster. Våra reduktionsregler i avsnitt A5 (sid. A5.1) antages tillämpbara. Efter reduktion får vi nedanstående ekvivalenta småsignalschema, vars framtagande läsaren ordentligt begrundar (jämför sid. B8.1).

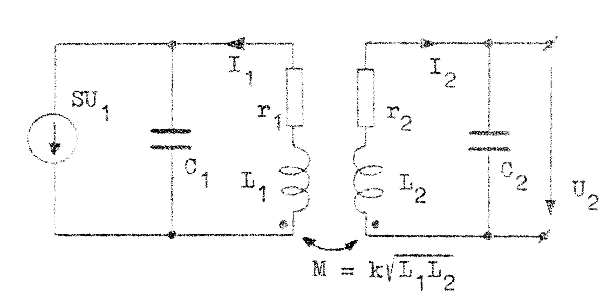I vidstående fig. F4.12 har följande storheter införts:

	F4.37a
	F4.37b
	F4.37c
	F4.37d
	F4.37e

Fig. F4.12. Ekvivalent småsignalschema för steget i fig F4.11. Jämför fig. B8.2, sid. B8.1.

Ett studium av detta steg innebär i huvudsak att vi studerar egenskaperna hos två induktivt kopplade resonanskretsar, något som vi gjort relativt ingående i avsnitt B8. Jämför vi fig. F4.12 med fig. B8.2 (sid. B8.1), finner vi, att dess figurer (schemor) blir identiska, om vi i fig. B8.2 sätter I_k = SU₁. Detta innebär, att alla resultat i avsnitt B8 kan utsträckas att gälla för vårt dubbelavstämda förstärkarsteg. I den mån storheterna I_k, E, R_I och R_II förekommer i B8-avsnittets ekvationer och formler, skall dessa bytas mot

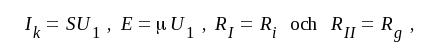F4.38

något som torde vara uppenbart efter studium av fig. F4.11 och fig. B8.1.

Komplexa förstärkningen definierar vi här som

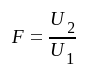F4.39

medan överföringsfunktionen F i avsnitt B8 definieras som U₂/E. Eftersom E = μU₁, erhålles tydligen det dubbelavstämda stegets förstärkning efter multiplikation av motsvarande förstärkningsuttryck i avsnitt B8 med storheten μ (=SR_i).

Vi har sålunda redan utrett det dubbelavstämda stegets väsentliga egenskaper och läsaren hänvisas därför till avsnitt B8. Här inskränker vi oss till att något beröra det enklaste av de fall, som behandlats i B8-avsnittet, nämligen fallet med lika resonansfrekvenser och lika stora Q-värden hos de båda kretsarna i fig. F4.12 (jämför sid. B8.7). Vi förutsätter dessutom, att L₁ = L₂ och att C₁ = C₂.

Med ledning av sambandet B8.21 (sid. B8.7) och med hänsynstagande till uttrycken F4.38 erhålles

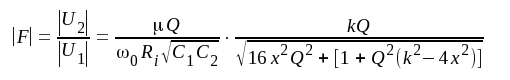F4.40

där vi infört beteckningen ω₀ för kretsarnas gemensamma resonansvinkelfrekvens (i stället för ω_m i avsnitt B8). Vi förenklar uttrycket F4.40 genom att införa

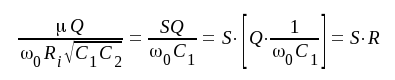F4.41

där R = totala parallellresistansen hos vardera kretsen.

Enligt uttrycket för x (sid. B8.3) gäller att

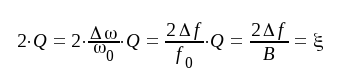F4.42

där vi analogi med beteckningen i föregående avsnitt infört den normerade frekvensvariabeln ξ (jämför sambanden F4.9 eller F4.30). B är kretsarnas lika stora bandbredder och Δf = f - f₀ på vanligt sätt.

För att ernå en ytterligare förenkling av våra uttryck inför vi storheten ℋ , som vi lämpligen kallar kopplingstalet:

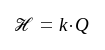F4.43

Med ovanstående beteckningar (F4.41, F4.42 och F4.43) får uttrycket för förstärkningen (f4.40) den enkla formen:

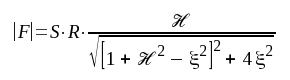F4.44

Läsaren visar själv, att detta uttryck även kan skrivas under formen:

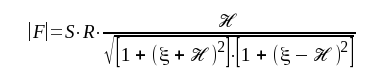F4.45

Jämför vi F4.45 med sambandet F4.31, finner vi, att de båda uttryckens nämnare helt överensstämmer, om vi sätter m = ℋ. Vi drar härav slutsatsen, att det dubbelavstämda steget har samma form på transmissionskurvan, som vår 2-stegs sicksack-avstämda förstärkare har. Kurvan blir "maximalt flat" för ℋ = 1 (kQ =1). Om ℋ > 1 blir kurvan dubbeltoppig och om ℋ < 1 blir kurvan enkeltoppig (jämför fig. B8.5, sid. B8.7).

I fallet ℋ = 1 blir maximalförstärkningen (sätt ξ = 0 i sambandet F4.44).

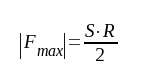F4.46

Ju större vi gör ℋ (vi förutsätter ℋ > 1), desto större blir avståndet mellan topparna. Samtidigt blir emellertid dalen i bandmitten djupare. Denna dal kan vi fylla ut genom att koppla ett enkelavstämt steg (eller ett bandfiltersteg med annan kopplingsfaktor) i kaskad. Vi kan på så sätt få en relativt bredbandig och flat transmissionskurva.

Inledningsvis nämdes att vi även kan tänka oss kapacitiv koppling mellan de båda resonanskretsarna. I ett dylikt fall skulle schemat i fig. F4.12 få nedanstående utseende (fig. F4.13). C₀ benämner vi kopplingskapacitansen.

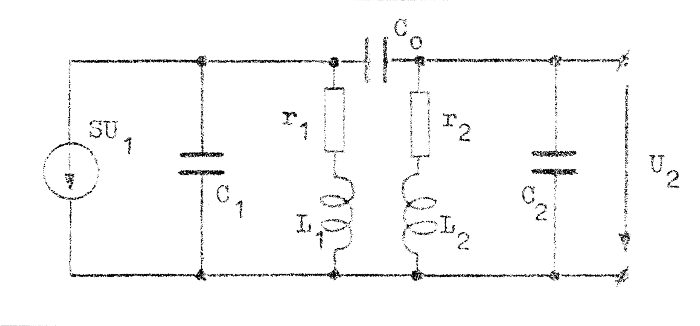		Även i detta fall kan man visa, att man får en transmissionskurva av den typ, som den sicksackavstämda 2-stegs förstärkaren har. Bandbredd och toppavstånd bestämmes i detta fall av kopplingskapacitansen C₀. Ingenting väsentligt ändras om C₀ utbytes mot en lämplig kopplingsinduktans L₀.
Fig. F4.13. Ekvivalent småsignalschema vid kapacitiv koppling mellan resonanskretsarna.

link >