< link link link >


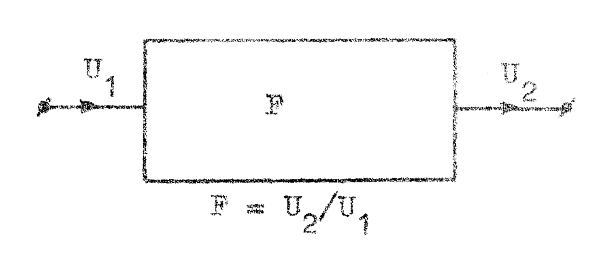
    Vi skall här studera inverkan av drift i flerstegsförstärkare och vi beskriver därvid en driftfri förstärkare (eller ett driftfritt förstärkarsteg) i enlighet med blockschemat i fig. F5.7, där U₁ och U₂ är in- respektive utsignal i komplex form där F = U₂ / U₁ = komplexa förstärkningen.

		Eftersom en LS-förstärkare kan arbeta med både lik- och växelsignaler, räknar vi lämpligen med komplexa spännings- och strömstorheter på samma sätt som i fråga om exempelvis RC-förstärkare. Systemets beteende ur likspännings-signal-synpunkt erhålles genom att vi i våra räkningar
Fig. F5.7. Blockschema för LS-förstärkare utan drift.

låter vinkelfrekvensen sss. Vi får här ej glömma, att U₁ och U₂ (respektive ögonblicksvärdena u₁ och u₂) är på vilovärdena överlagrade signaler, vilket är särskilt viktigt att ihågkomma, då signalfrekvensen är noll (likspänning).

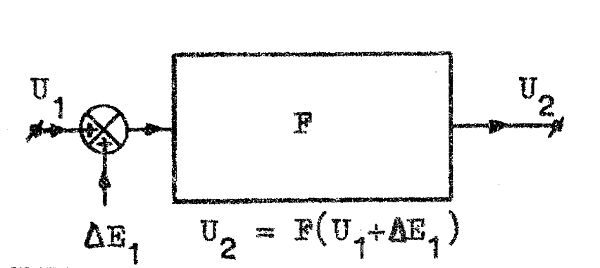
    Låt oss nu betrakta en LS-förstärkare enligt fig. F5.8, där vi antagit, att förstärkarens driftspänning hänförd till ingången är ΔE₁ (komplex form; driftspänningen kan, om vi så vill, betraktas som en synnerligen långsamt varierande sinusformad växelspänning). Att driftspänningen är hänförd till ingången kräver en kommentar: antag, att förstärkaren är balanserad, d.v.s. totala utspänningen är noll, då insignalen är noll (kortsluten ingång). Efter viss tid (alltjämt med insignalen noll) har utspänningen nått ett visst värde  sss U₂ på grund av drift i förstärkaren. För att återföra utspänningen till noll kan vi på ingången lägga spänningen

		-ΔE1, där ΔE1 = ΔU2/F. Vi kan därför även tänka oss, att driften förorsakas av en spänning +ΔE1 på ingången. Driftspänningen ?E1 uttrycker då den verkliga förstärkarens drift hänförd till ingången. Driften på utgången är sss.
Fig. F5.8. Blockschema för LS-förstärkare med drift.

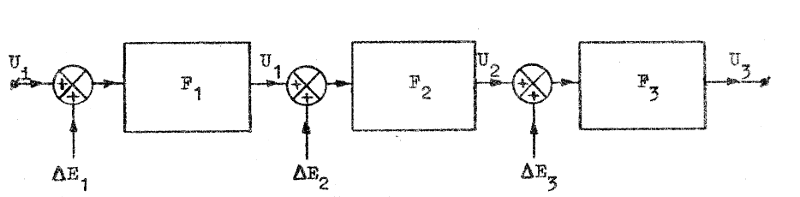
    Låt oss så kaskadkoppla tre steg (eller tre förstärkare) med komplexa förstärkningen F₁, F₂ och F₃ (fig. F5.9). Stegens driftspänningar, hänförda till respektive förstärkaringångar, är ΔE₁, ΔE₂ och ΔE₃.

	Fig. F5.9. Blockschema för trestegs LS-förstärkare med drift.

    Om insignalen är U_i och utsignalen är U₃ erhålles direkt med ledning av fig. F5.9:

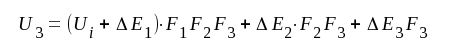F5.3

    Sätter vi U₃ = 0 i sambandet ovan erhålles:

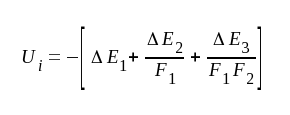F5.4

    U_i i sambandet F5.4 är den spänning, som erfordras på första stegets ingång, för att utspänningen (U₃) på sista steget skall bli noll. Hela förstärkarens drift ΔE, hänförd till ingången, blir sålunda:

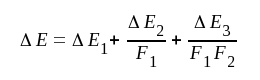F5.5

    Resultatet F5.5, som utan vidare kan utsträckas att gälla ett godtyckligt antal steg, visar, som väntat, att första stegets drift dominerar. Vi skulle tydligen komma idealet ganska nära, om första stegets drift kunde göras mycket liten och om första stegets förstärkning samtidigt kunde göras mycket stor.

    Vi skall i ett kommande avsnitt finna, att det möjligt att konstruera helt driftfria LS-förstärkare med extremt hög förstärkning. De har dock en allvarlig nackdel: redan vid frekvenser av storleksordningen någon Hz faller förstärkningen mycket snabbt. Om en dylik förstärkare användes som för-förstärkare kan de följande stegens bidrag till driften göras mycket litet. Om blocket F₁ i fig F5.9 får vara en dylik förstärkare, blir ΔE₁ = 0 i sambandet F5.5 och övriga termer blir mycket små under förutsättningen att │F₁│ är mycket stort. Totalförstärkningen │F₁F₂F₃│ blir på grund av │F₁│ starkt frekvensberoende, något som vi kan tänkas bota med motkoppling i enlighet med fig. F5.10 nedan.

	Fig. F5.10. Blockschema för trestegs motkopplad LS-förstärkare med driftfritt första steg.

    Komplexa förstärkningen F' = U₃ / U_i för den motkopplade förstärkaren blir (jämför sid. F3.2):

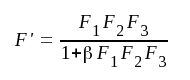F5.6

    Så länge │β F₁F₂F₃│ >> 1,  är

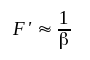F5.7

d.v.s. vi får en någorlunda konstant förstärkning (återkopplingskvoten förutsättes vara konstant).

    Motkopplingen har alltså här till uppgift att hålla förstärkningen approximativt konstant inom ett större frekvensområde. Däremot minskar motkopplingen i och för sig ej driften i en förstärkare.

Övning: Beräkna driftspänningen ΔE, hänför till ingången, för systemet i fig. F5.10, under förustättning att ΔE₁ ≠ 0. Tänkt igenom resultatet och jämför med sambandet F5.5.

    Synpunkter av det slag, som ovan framförts, ligger till grund för den bl.a som operationsförstärkare använda s.k. chopper-stabiliserade LS-förstärkaren.


link >