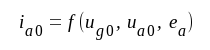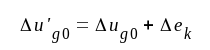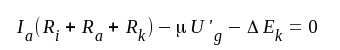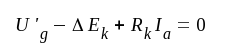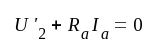< link link link >


    Med ett enkelt exempel skall vi här skissera, hur driften i ett steg kan uppskattas. Allmänt kan sägas att vi i driftproblem arbetar med små spännings- och strömändringar, som förorsakas av likaledes små ändringar i systemets (stegets) parametrar (t.ex. matningsspänningar). I fråga om små ändringar beter sig systemet i huvudsak linjärt och vi kan därför uppskatta totala driften genom superposition av bidragen från de olika driftorsakerna.

    Innan vi övergår till vårt egentliga exempel skall vi beröra hur vi räknemässigt tar hänsyn till glödspänningsändringarnas inverkan.

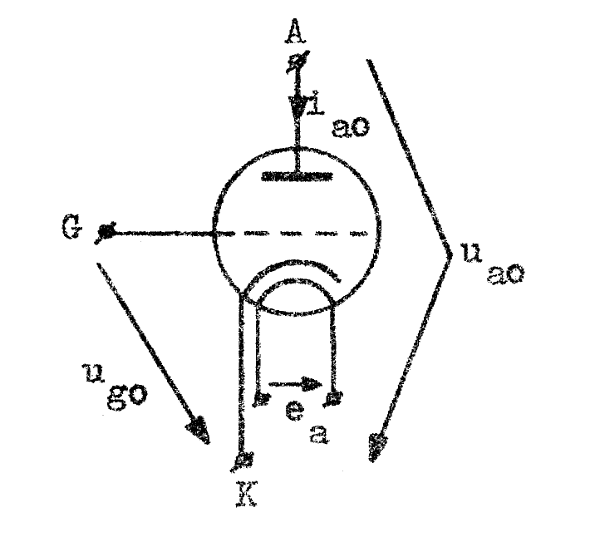		Vi betraktar en triod enligt fig. F5.11, för vilken vi helt allmänt sätter: F5.8 d.v.s. vi förutsätter, att triodens anodström är en funktion av spänningarna ug0 och ua0 samt glödspänningen ea (jämför avsnitt C2.09, sid. C2.22).     Vi ger storheterna ug0, ua0 och ea de små tillskotten Δug0, Δua0 och Δea respektive. ia0 får då tillskottet
Fig. F5.11.

F5.9

eller

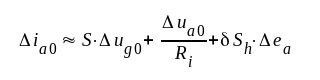F5.10

där vi infört rörparametrarna S och R_i samt den nya parametern S_h genom definitionen

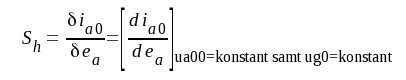F5.11

    Storheten S_h kan vi med ledning av sambandet F5.11 lätt bestämma experimentellt.

    Vi multiplicerar sambandet F5.10 med R_i och får

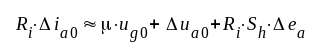F5.12

    Vi dividerar och multiplicerar sista termen i sambandet F5.12 med (1+μ) och får

F5.13

    Slutligen inför vi den kortare beteckningen

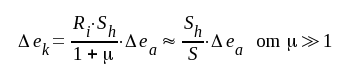F5.14

    Därmed kan sambandet F5.13 skrivas på följande sätt:

F5.15

		Sambandet F5.15 kan vi tolka som ekvationen för ekvivalentschemat i fig. F5.12, där     Schemat innebär i princip, att en glödspänningsändring (Δea) beskrives som en ekvivalent emk (Δek) inkopplad mellan katoden (K') och katodkontakten (K). Enligt sambandet F5.14 är Δek proportionell mot Δea. För oxidkatodrör är Δek av storleksordningen ±0,1 volt om Δea = ±10 % av ea.
Fig. F5.12. Triodens ekvivalentschema med hänsyn tagen till inverkan av glödspänningsändringar.

    Efter denna inledning skall vi uppskatta driften i ett elementärt steg enligt fig. F5.13. För att inte göra exemplet alltför oöverskådligt inskränker vi oss till en beräkning av den drift, som varierande glöd- och anodbatterispänning introducerar.

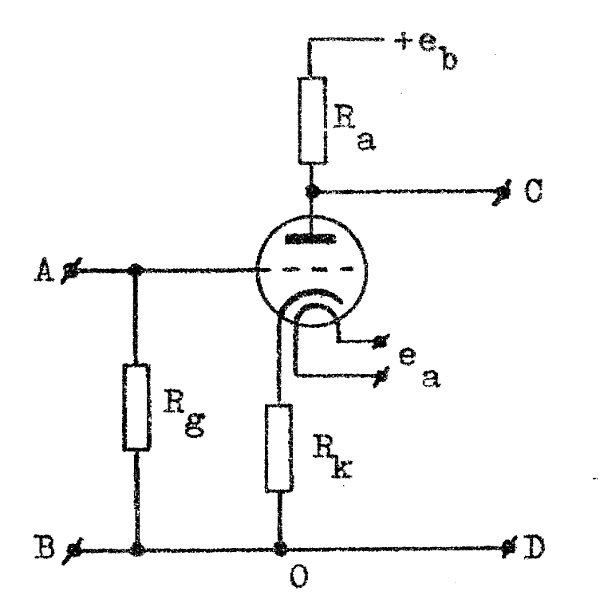		Av samma skäl är steget ej balanserat, d.v.s. spänningen mellan utklämmorna ej noll, då inspänningen är noll.     Vi antar först, att spänningen mellan utklämmorna har ett visst bestämt värde, då inspänningen är noll, d.v.s. då ingången är kortsluten. Problemet är att beräkna ändringen i utspänning, då glödspänningen ändras med Δea och och anodbatterispänningen med Δeb, och även att omräkna denna ändring till ekvivalent inspänningsändring.
Fig. F5.13

    Vi begagnar vårt nya ekvivalentschema fig. F5.12, och vi kan, om vi så önskar, alltjämt räkna i komplex form (jämför sid. F5.7). Därmed fär schemat ett utseende enligt fig. F5.14, där ΔE_k förorsakas av glödspänningsändring och där ΔE_b representerar ändringen i anodbatterispänning.

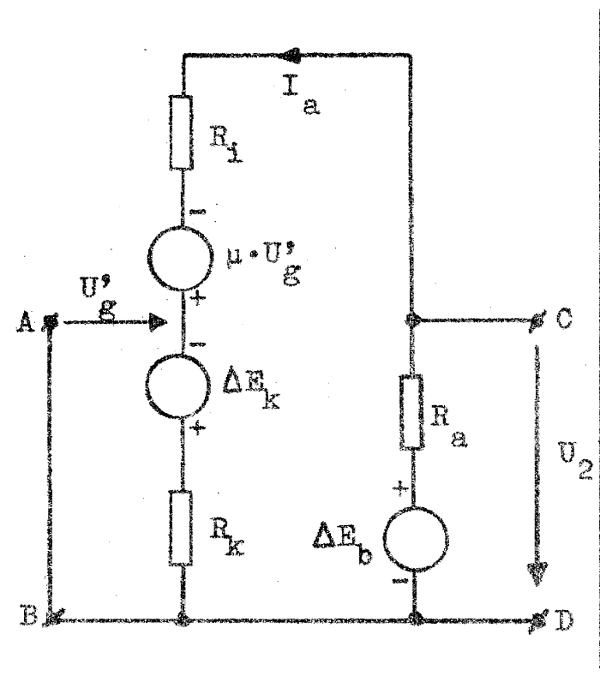		Vi använder superpositionsatsen och beräknar först den utspänning U'2 som förorsakas av ΔEk och därefter den utspänning U''2 som föranledes av ΔEb, d.v.s. vi spaltar vår beräkning i två delar a) och b) enligt nedan.     a) ΔEb = 0, ΔEk ≠ 0.     Vi uppställer följande ekvationer: F5.16 F5.17 F5.18     Eliminering av U'g och Ia ur ekvationssystemet ovan ger:
Fig. F5.14. Ekvivalentschema för driftberäkning.

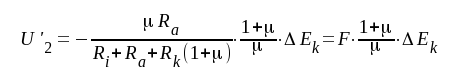	F5.19

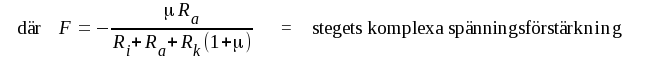    Om driftspänningen U'₂ hänförs till ingången erhålls

F5.20

    I ögonblicksvärdesform (=likspänningsform) erhålles

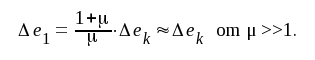F5.21

    Om vi alltså mellan inklämmorna (A och B i fig. F5.13) inkopplar spänningen -Δe₁ (A negativ relativt B) kommer spänningen mellan utklämmorna (C och D) att återföras till utgångsvärdet (värdet före glödspänningsändringen).

    b) ΔE_b ≠ 0, ΔE_k = 0.

    Med ledning av fig. F5.14 får vi nu ekvationerna:

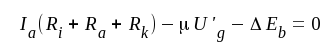	F5.22
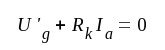	F5.23
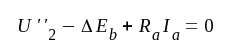	F5.24

    Eliminering av U'_g och I_a ger

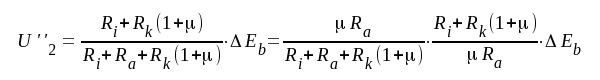F5.25

som med ledning av förstärkningsuttrycket på föregående sida även kan skrivas  på följande sätt:

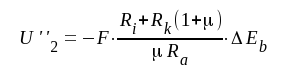F5.26

    Hänföres driftspänningen U''₂ till ingången erhålles

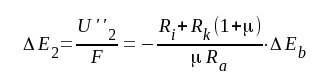F5.27

    Övergång till momentanvärden ger

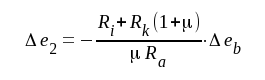F5.28

    Om Δe_k och Δe_b har samma tecken, d.v.s. om glödspänningen e_a ökar samtidigt med anodbatterispänningen e_b, så kommer enligt sambanden F5.21 och F5.28 Δe₁ och Δe₂ att få olika tecken och de båda driftspänningarna kan sålunda unde speciellt lyckliga omständigheter kompensera varandra. Om emellertid Δe_k och Δe_b är helt oberoende av varandra, så blir den maximalt tänkbara driften, hänförd till ingången,

F5.29

och den maximala driften på utgången blir givetvis │F│∙│Δe│.

    Det överlåtes åt läsaren att på egen hand undersöka inverkan av ändringar i komponentvärden och rörparametrar.

Sifferexempel: Schema enligt fig. F5.13 med e_b = 250 V, e_a = 6,3 V, R_a = 50 kΩ och R_k = 1,5 kΩ.

    Röret antages vara typ 6SN7GT, som med ledning av rördiagram och ovannämda data kan visas få vilopunkten u_a00 ≈ 112 V, u_g00 ≈ -4 V och i_a00 ≈ 2,7 mA, d.v.s. u_CD0 ≈ 116 V (utklämspänningen i vila).

    I nämnda vilopunkt har röret följande parameterdata:

    R_i ≈ 13 kΩ, u ≈ 20 , S ≈ 1,5mA/V och S_h ≈ 0,25mA/V.

    Vi antar, att Δe_a ±5 %, av 6,3 V = ±0,32 V och att Δe_b ±1 %, av 250 V = ±2,5 V.

    Vi beräknar först Δe_k ur sambandet F5.14:


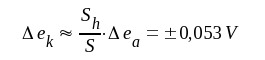    Ur sambanden F5.21 respektive F5.28 erhålles


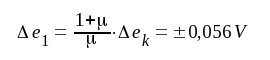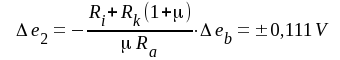    Slutligen blir


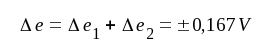    Stegets spänningsförstärkning beräknas till ssss. Utspänningen kan alltså driva högst ssss volt under förutsättning att ändringarna i e_a och e_b uppgår till maximalt ±5% respektive ±1%. Δe₁ har samma tecken Δe_k (eller Δe_a) medan Δe₂ och Δe_b har olika tecken Om e_a och e_b erhålles från samma nätaggregat, kan vi normalt förutsätta, att e_a och e_b ökar eller minskar samtidigt, vilket i detta fall bör medföra en driftkompenserande effekt.


link >