< link link link >


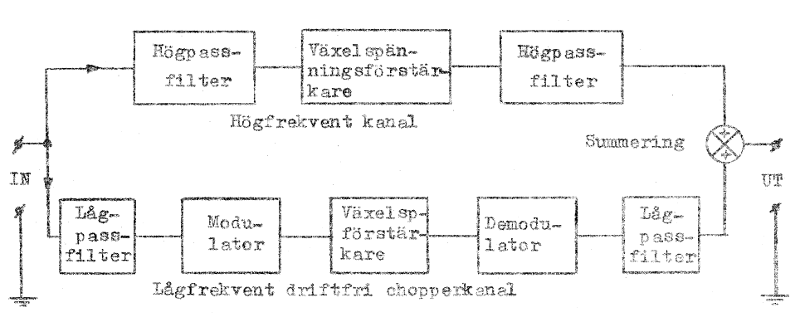
    Vi har i föregående avsnitt funnit, att chopperförstärkare är användbar för LS och extremt låga frekvenser. Önskar vi driftfrihet men dessutom förstärkning inom ett relativt brett frekvensband, inkluderande frekvensen noll, skull vi kunna tänka oss ett arrangemang enligt fig. F5.27, där signalvägen spaltas upp i en lågfrekvent driftfri chopperkanal och en högfrekvent kanal. Signalerna från de olika kanalerna summeras i en krets, som exempelvis kan vara ett differentialsteg (om vi låter fasvridningen i ena kanalen vara noll och i andra 180°;  jämför sambandet F5.34). Genom omsorgsfull dimensionering (och utnyttjande av motkoppling) är det på ovan skisserat sätt möjligt att bygga förstärkare med nästan konstant förstärkning inom ett brett frekvensband, som inkluderar frekvensen noll, samtidigt som driften är eliminerad.

	Fig. F5.27. Tvåkanalig bredbandig LS-förstärkare.

    I många tillämpningar (t.ex. operationsförstärkare för analogimaskiner) är det ej nödvändigt att förstärkningen är konstant vid alla frekvenser. Motkoppling användes alltid i dessa förstärkare och det verkligt viktiga kravet är minimal drift. De synpunkter, som framfördes i avsnitt F.04 (sid. F5.7), kan läggas till grund för en förstärkarkonstruktion. Förstärkaren enligt fig. F5.27 kan användas som en driftfri för-förstärkare med stor förstärkning (jämför blocket F₁ i fig. F5.9 respektive blocket F₁ i fig. F5.10, sid. F5.8 och F5.9). Eftersom hög förstärkning i första hand erfordras för att bemästra driftproblemet (se sambandetF5.5; ΔE₁ = 0 och │F₁│ >> 1 ger en praktiskt taget driftfri förstärkare), kan den högfrekventa kanalen i fig. F5.27 ersättas med en ren förbikoppling (= en gångs förstärkning). Summationskretsen kan sedan följas av ett eller flera direktkopplade LS-steg, så att totalförstärkningen blir så stor, att förstärkningen vi motkoppling helt bestämmes av motkopplingsfyrpolen.

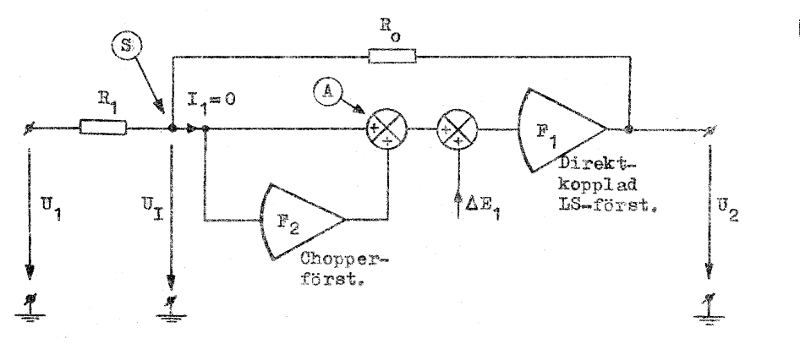
    Med en chopper-stabiliserad LS-förstärkare (Goldberg-förstärkare) menar vi en LS-förstärkare uppbyggd enligt ovan skisserad princip. Ett principschema för en som teckenvändare (om R₀ = R₁; jämför fig. F3.29, sid. F3.27) kopplad dylik förstärkare visas i fig. F5.28, där vi med tanke på en följande beräkning infört driftspänningen ΔE₁ hos den konventionella direktkopplade LS-förstärkaren (F₁ i fig. F5.28). Blocket F₂ representerar den driftfria chopperförstärkaren, som har mycket stor förstärkning (vid LS och extremt låga frekvenser).

	Fig. F5.28. Chopperstabiliserad LS-förstärkare, kopplad som teckenvändare.

    Låt oss kortfattat beröra den chopperstabiliserade LS-förstärkarens drift. Vi förutsätter, att inimpedansen är så hög, att I₁ = 0 i fig. F5.28. Strömmen genom R₁ och strömmen genom R₀ blir då lika stora och vi får:

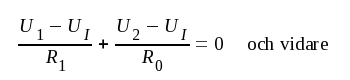	F5.38
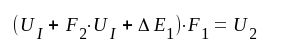	F5.39

    Elimineras U_I ur ekvationssystemet erhålles:

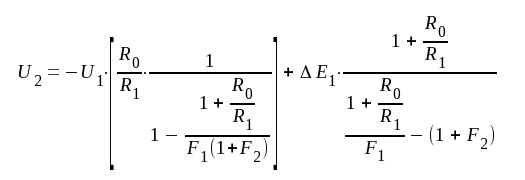F5.40

     Vårt primära intresse är här driften. För enkelhets skull låter vi R₀ vara lika med R₁ (R₀ = R₁ innebär ren teckenvändning) och vidare antar vi, att │F₁│ >> 1 och att │F₂│ >> 1 vid extremt låga frekvenser (driften är ett LS eller lågfrekvent fenomen). Under dessa förutsättningar blir

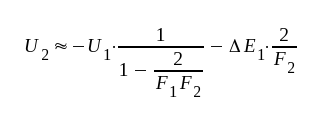F5.41

    Utan chopperstabilisering, d.v.s. F₂ = 0, erhålles

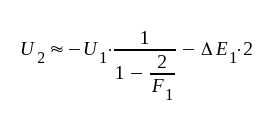F5.42

    Jämför vi sista termen (drifttermen) i sambandet F5.41 med sista termen i F5.42, finner vi, att drifttermens storlek blir│F₂│gånger mindre med chopper-stabilisering, en ofantlig vinst.

    I en operationsförstärkare på spänningen (U_I) i summationspunkten (s i fig. F5.28) alltid praktiskt taget noll. Så gott som alla fel, inklusive drift, som kan uppstå i en dylik förstärkare, ger sig till känna som en onormal spänning i summationspunkten. Chopperstabiliseringen strävar just  att hålla spänningen i summationspunkten lika med noll.

    Chopperstabilisering i en operationsförstärkare innebär sammanfattningsvis

    a) en avsevärd reducering av driften,
    b) en ökning av den öppna förstärkarens förstärkning vid låga frekvenser med en faktor på 1000 - 5000 och
    c) att vi slipper nollställa förstärkaren manuellt

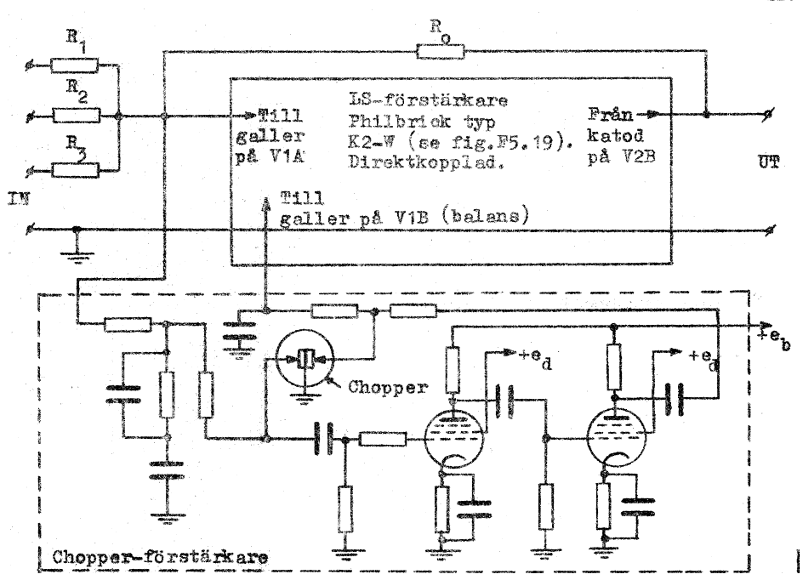
    Slutligen skisseras nedan ett schemaexempel på en chopperstabiliserad operationsförstärkare (summator). Som F₁-förstärkare (jämför fig. F5.28) begagnar vi Philbrick-förstärkaren i fig. F5.19. Denna förstärkare första förenklade differentialsteg tjänstgör som summeringskrets (motsvarande summeringssymbolen A i fig. F5l28).

	Fig. F5.29. Schemaexempel på en chopperstabiliserad summatorkopplad operationsförstärkare. Disskussionsunderlag.

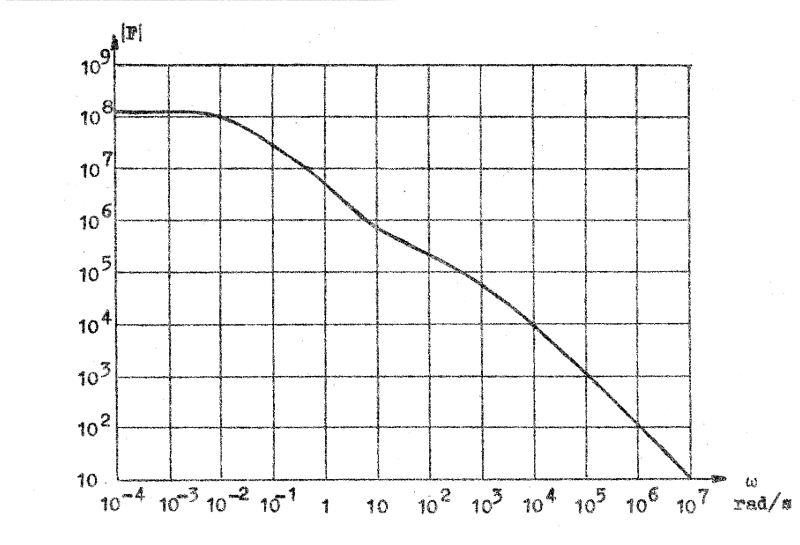
    Den öppna förstärkningen (R₀ urkopplad) hos en chopper-stabiliserad förstärkare av den typ, som skisserats i fig. F5.29 ovan, kan variera med frekvensen på ett sätt, som framgår av nedanstående fig. F5.30.

	Fig. F5.30. Exempel på frekvenskurva för öppen chopperstabiliserad förstärkare av den typ, som visas i fig. F5.29.

link >