< link link link >

    Låt oss betrakta en homogen parledning med de primära konstanterna r, l, g och c. Ledningen matas mellan sina ingångsklämmor A och B (fig. J1.1) av en sinusspänning u₁ = │U₁│∙ sinωt, d.v.s. motsvarande

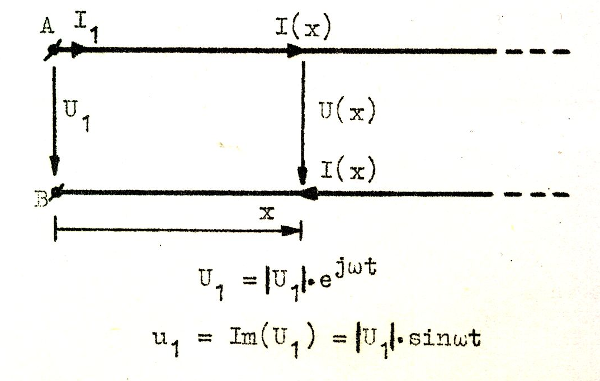		komplexa spänningen är U1 = U1 ⋅ ejωt och vi har             u1 = Im(U1) Vi antager, åtminstone tills vidare, att ledningen är oändligt lång. x är en koordinat längs ledningen (definierad positiv ut på ledningen; ledningens närända definieras av x = 0).
Fig. J1.1.

    Spänning och ström måste rimligtvis vara funktioner av x (och t). Komplex spänning och ström i planet x betecknar vi U(x) och I(x). Vår uppgift är att söka bestämma U(x) och I(x) samt de häremot svarande ögonblicksvärdena u(x) och i(x).

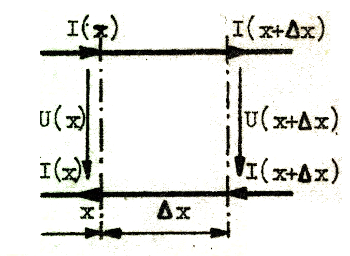
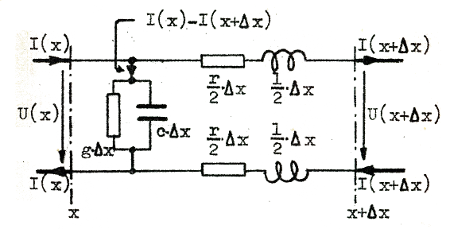
    Ett litet ledningsstycke med längden Δx bör vi kunna betrakta som ett diskret element med serieresistansen r ∙ Δx, och induktansen l ∙ Δx, parallellkonduktansen g ∙ Δx och kapacitansen c ∙ Δx i överensstämmelse med fig J1.2 och J1.3 nedan.

Fig. J1.2.	Fig. J1.3.

     Kirschoffs första lag, tillämpad på schemat fig. J1.3, ger


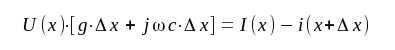varur vi får



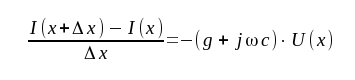som efter limesövergång Δx ⇾ 0 ger

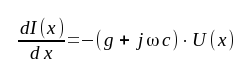J1.1

    Med tillämpning av Kirschoffs andra lag erhålles


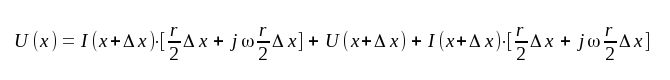eller


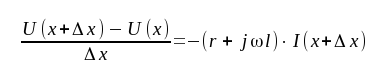som efter limesövergång Δx ⇾ 0 ger

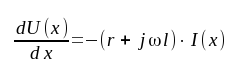J1.2

    Vi deriverar J1.2 och får

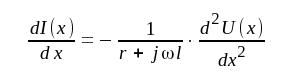J1.3

    J1.3 insättes i J1.1. Vi får då

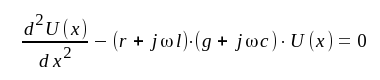J1.4

    För att få en enklare ekvation inför vi storheten γ , definierad av sambandet

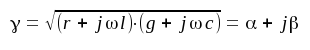J1.5

där vi infört ytterligare två nya storheter, nämligen


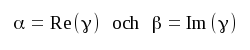    Med dessa nya beteckningar övergår J1.4 i den formellt enklare ekvationen

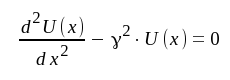J1.6

    Läsaren kontrollerar själv att eliminering av U(x) mellan ekvation J1.1 och J1.2 ger ekvationen

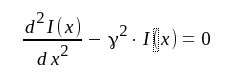J1.7

    Såväl komplex spänning som ström på ledningen styres sålunda av en och samma differentialekvation (J1.6 respektive J1.7). Denna, som är linjär, homogen differentialekvation av andra ordningen, benämner vi telegrafekvationen.

    Från matematiken vet vi, att den allmänna lösningen till J1.6 respektive J1.7 har formen

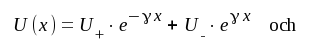	J1.8
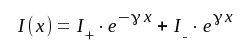	J1.9

där U₊, U_-, I₊ och I_- är komplexa konstanter, som från fall till fall måste bestämmas. Sambanden J1.8 och J1.9 är emellertid ej oberoende av varandra, vilket framgår av J1.1 och J1.2. Vi deriverar J1.8 med avseende på x och får med hjälp av J1.2

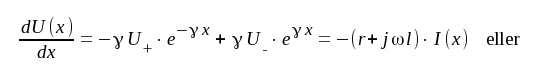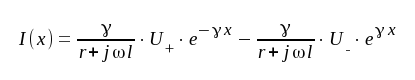	J1.10

    I J1.10 är


där vi infört storheten Z₀, definierad av sambandet

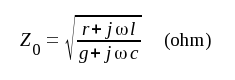J1.11

    Med J1.11 övergår J1.10 i uttrycket

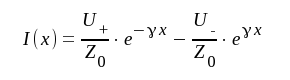J1.12

    Jämför vi J1.12 och J1.9 ser vi, att

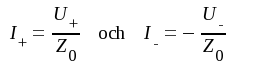
    Vi sammanfattar:

	J1.13
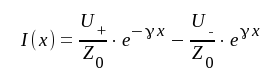	J1.14
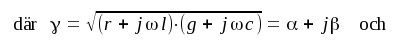	J1.15
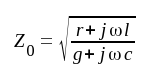	J1.16

    De ovan införda nya storheterna γ, α, β och Z₀ utgör ledningens s.k. sekundära konstanter, som benämnes enligt nedan.

γ = ledningens gångkonstant (1/m)
α = ledningens dämpningskonstant (neper/m)
β = ledningens faskonstant (radianer/m)
Z0 = ledningens komplexa egenimpdedans (ohm)

  I litteraturen finner man för Z₀ även benämningen (komplex) vågimpedans, karakteristisk impedans eller blott karakteristik. För storheten γ ser man stundom benämningen fortplantningskonstant.


link >