< link link link >

Enligt J1.13 är uttrycket på den komplexa spänningen på ledningen i ett godtyckligt plan x

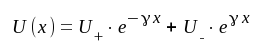J1.17

Vi måste nu söka bestämma konstanterna U₊ och U_-. Dessa konstantvärden beror av den spänning, som matar i ledningens närända, och av den belastningsimpedans, som är placerad i ledningens fjärrända, d.v.s. konstanterna bestämmes av ledningens randvillkor. Enligt vår hittillsvarande förutsättning är komplexa spänningen mellan ledningens ingångsklämmor U₁ = │U₁│⋅ e^jωt, varför vi med J1.17 får

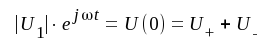J1.18

Vi har i avsnitt 1.03 förutsatt, att ledningen är oändligt lång. Sista termen i J1.17, som lyder

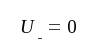skulle då för stora x-värden (på grund av faktorn e^αx; α är en positiv reell kvantitet) växa till ett mycket stort värde, vilket är fysikaliskt orimligt för en ledning, som matas i närändan (x = 0). Vi måste därför sätt

J1.19

Av J1.18 och J1.19 följer, att

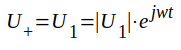J1.20

Därmed är U₊ och U_- bestämda i detta fall (oändligt lång ledning). Insättning i J1.19 och J1.20 i J1.13 och J1.14 ger

J1.21

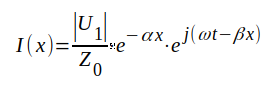J1.22

Komplexa spänningen och strömmen är därmed bestämd överallt på ledningen för fallet oändlig lång ledning. Eftersom vi från början förutsatt, att u₁ = Im(U₁) erhålles spänningens och strömmens ögonblicksvärden lätt ur J1.21 och J1.22.

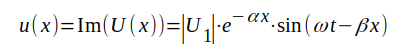J1.23

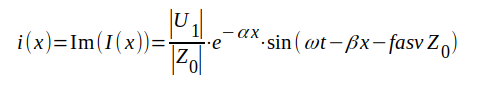J1.24

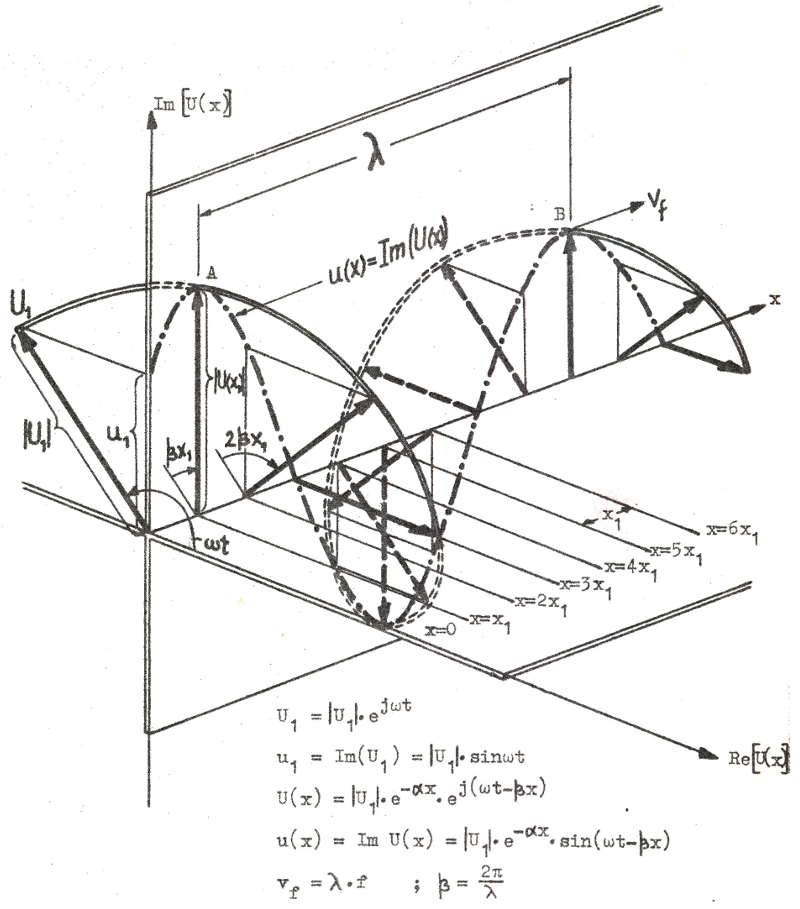
Låt oss nu rita komplexa spänningen U(x) i komplexa talplanet för olika diskreta värden på x (x = 0, x = x₁, x = x₂, x = x₃ o.s.v.) men för ett och samma fixa värde på tiden t. Komplexa talplanet parallellförflyttas därvid lämpligen i tur och ordning till x-värdena x = 0, x = x₁, x = 2x₁ o.s.v.. Vi får då representationen i överensstämmelse med fig. J1.4 nedan.

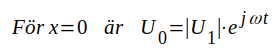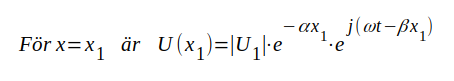De komplexa spänningsvisarnas spetsar ligger tydligen på en spiral, som med avtagande radie är lindad runt x-axeln. Eftersom u(x) = Im(U(x)) är vidare spänningens ögonblicksvärde denna spirals projektion på det plan, som bildas av imaginära axeln och x-axeln. Ögonblicksvärdet (spiralens projektion enligt ovan) är i fig. J1.4 utritad som en punkt-streckad kurva. Vi ser, att ögonblicksvärdet i exempelvis planet x = x₁ är positivt, medan det samtidigt i exempelvis planet x = 4x₁ är negativt. Låter vi nu tiden öka, kommer spiralen att rotera kring x-axeln och den punkt-streckade kurvan kommer att med avtagande amplitud förskjutas mot allt större x-värden. Det är med hänvisning till fig. J1.4 rimligt att säga, att spänningen utbreder sig på ledningen som en våg, som fortskrider i x-axelns positiva riktning. Enligt ekvation J1.22 eller J1.24 är det tydligt, att strömmen utbreder sig som en strömvåg på liknande sätt, men att denna våg på grund av Z₀ är fasförskjuten i förhållande till spänningsvågen. Kvoten mellan den komplexa spänningen U(x) och den komplexa strömmen I(x) i den fortskridande spänning-strömvägen är (se sambanden J1.21 och J1.22) överallt på ledningen lika med komplexa egenimpedansen Z₀.


	Perspektivisk representation av en framgående spänningsvåg. Fig. J1.4

    Första termen i J1.13 respektive första termen i J1.14 tolkar vi alltså som en spännings- respektive strömvåg, som utbreder sig i x-axelns positiva riktning. Vi benämner i fortsättningen dessa termer framgående spännings- respektive strömvåg.

    Enligt vårt resonemang ovan torde det nu var tydligt, att andra termen i J1.13 och J1.14 betyder en spännings- respektive strömvåg i x-axelns negativa riktning, d.v.s. med gångriktning från stora mot små x-värden. Dessa vågor benämner vi återgående spänningsvåg och återgående strömvåg respektive. När vi studerat orsaken till uppkomsten av en återgående våg inför vi för denna även benämningen reflekterad våg.

    Har vi på en ledning samtidigt både framgående och återgående våg uppstår på ledningen en s.k. stående våg, varom mera i ett kommande avsnitt.

    Slutligen betonar vi, att endast framgående våg existerar på en oändligt lång ledning.

link >