I avsnitt 1.04 har vi konstaterat, att komplexa spänningen och komplexa strömmen i en framgående våg alltid står i det fixa förhållandet Z0 till varandra, d.v.s. detta förhållande är för ledningen en egenskap, som entydigt bestämmes av ledningens primära konstanter. Kvoten mellan komplex spänning och komplex ström i en återgående våg är likaledes bestämt av egenimpedansen Z0. Det är synnerligen viktigt, att man ihågkommer denna fundamentala egenskap hos en fram- respektive återgående våg.
För den oändligt långa ledningen är enligt J1.21 och J122
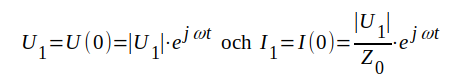 |
Den oändligt långa ledningens komplexa ingångsimpedans blir sålunda
 |
J1.25 |
eller i ord uttryckt: den oändligt långa ledningens ingångsimpedans är lika med egenimpedansen.
Med ledning av J1.25 och med hänvisning till fig. J1.5 och J1.6 kan vi göra följande enkla resonemang.
 |
 |
|
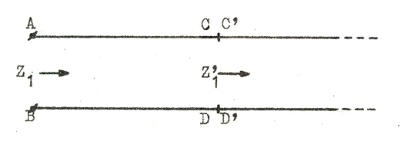
| Fig. J1.5 |
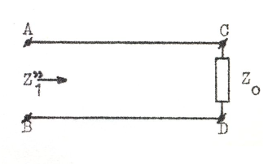
Fig. J1.6 |
Ledningen i fig. J1.5 förutsättes oändligt lång. Då blir tydligen ledningens komplexa ingångsimpedans Z1 = Z0. Om man skär av ledningen i punkterna C och D måste man mellan punkterna C' och D' se Z'1 = Z0.
Vi drager alltså slutsatsen, att en godtyckligt lång ledning, i fjärrändan avslutad med Z0, har ingångsimpedansen Z0. På denna ledning existerar endast en framgående våg.
En ledning, som i sin fjärrända är avslutad med belastningsimpedansen Z0 säges var reflexionsfritt avslutad och belastningen säges vara anpassad till ledningen.
För Z0 hade vi uttrycket
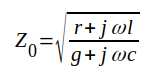 |
J1.26 |
Är ledningen förlustfri (r = 0 och g = 0) får vi
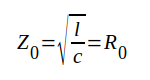 |
J1.27 |
där vi infört beteckningen R0 i avsikt att betona vågimpedansens resistiva karaktär. För R0 kan vi därför använda den alternativa benämningen vågresistans.
Vågimpedansen kan vara rent resistiv, även om ledningen ej är förlustfri (r ≠ 0 och g ≠ 0). Om nämligen de primära konstanterna har sådana värden, att
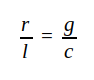 |
J1.28 |
 |
J1.29 |
En ledning, som har ovannämnda egenskap (J1.28) benämnes ofta Heaviside's ideala ledning.
Användes en ledning för ren likströmsöverföring (ω = 0) blir givetvis Z0 resistiv och lika med
En beräkning av Z0 ur givna data på de primära konstanterna kräver ett förhållandevis omfattande manuellt räknearbete. I många praktiska fall har ledningen sådana data, att man kan härleda approximativa formler för Z0.
Om sålunda ωl << r och g << ωc (gäller de flesta ordinära telefonkablar vid relativt låg frekvens) erhålles
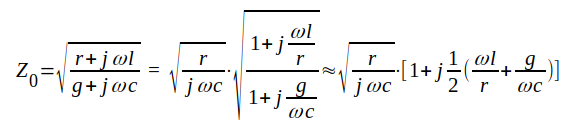 |
J1.30 |
Sista termen inom den stora parantesen är ofta så liten, att vi kan sätta
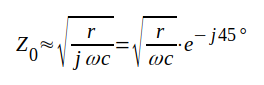 |
J1.31 |
Om å andra sidan r << ωl och g << ωc (gäller ofta ledningar vid radiofrekvens) erhålles
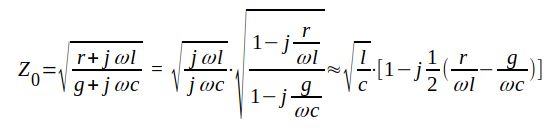 |
J1.32 |
Sista imaginära termen kan i många fall försummas och vi får då
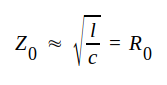 |
J1.33 |
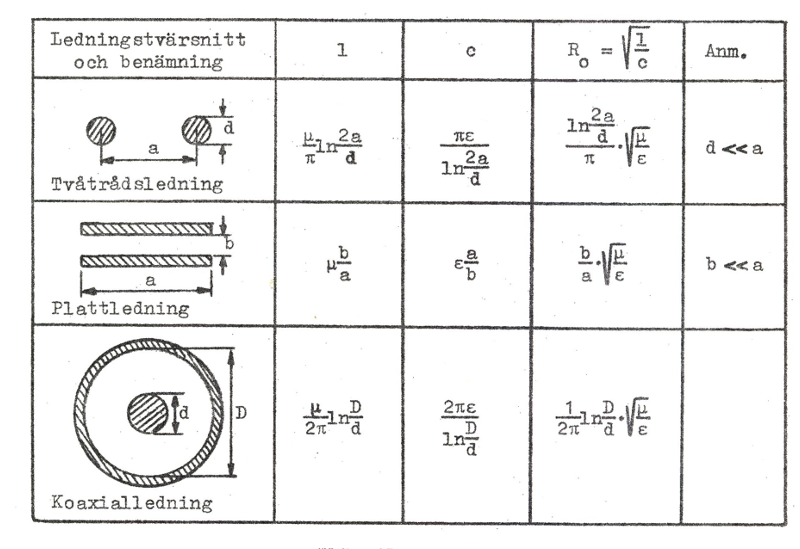
I tabellen nedan, fig. J1.7, ges data på l, c och R0 för tre enkla parledningar. μ = μr μ0 och ε = εr ε0.
| |
 |
|
| |
Fig. J1.7 |
|
link >