< link link link >

    Betraktar vi fig. J1.4 (sid. J1.7) ser vi, att den fortskridande vågens fas ändrar sig 360° på sträckan λ, varav följer att


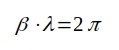    λ, som är avståndet längs ledningen mellan två plan, i vilka den fortskridande vågen har samma fasläge, benämner vi våglängden.

    Vi har alltså

J1.34

    β (1/m) är sålunda vågens fasvridning per längdenhet och vi anger därför lämpligen dess sort i radianer per meter.

    Den framgående vågens totala fas i planet x är ωt - βx. I exempelvis planet x = x₁ i fig. J1.4 är ωt - βx = 90°. För konstant fas fordras tydligen, att x ökar, då tiden ökar. Konstant fas betyder alltså, att


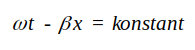    Vi deriverar med avseende på tiden t och får


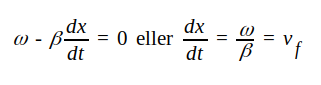    v_f är alltså den hastighet, varmed vi skall förflytta oss längs ledningen för att hela tiden se konstant fas (d.v.s. vi har då hela tiden i det med hastigheten v_f framrusande planet en ren likspänning, som dock på grund av dämpkonstanten a ständigt avtager). v_f benämer vi vågens fashastighet, som alltså bestämmes av sambandet

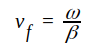J1.35

    J1.35 kan omskrivas på följande sätt

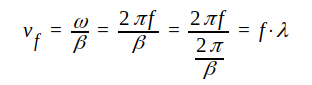J1.36

    J1.36 är det för all vågutbredning karakteristiska sambandet mellan frekvens, våglängd och fashastighet.

    Vi kan säga, att fashastigheten uttrycker den hastighet, varmed ett visst elektromagnetiskt tillstånd (konstant fas) fortskrider på ledningen. Observera slutligen v_f är den hastighet, varmed spiralens skärningspunkt (punkten A eller B i fig. J1.4) med (imaginäraxeln)-(x-axel)-planet rör sig i längdriktningen.

    För en återgående våg är totala fasen ωt + βx. För att denna skall vara konstant fordras att ωt + βx = konstant. Efter derivering får vi


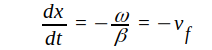d.v.s vågen rör sig från stora mot små x-värden.

    För en förlustfri ledning (r = 0, g = 0) gäller, att



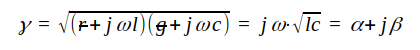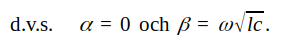    Fashastigheten blir sålunda

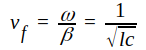J1.37

    För samtliga de i tabellen fig. J1.7 upptagna parledningarna blir lc = με, varav följer, att

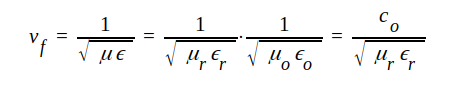J1.38

där  = ljushastigheten i vakuum. Befinner sig ledningen i vakuum (luft) är ε_r = 1 och μ_r = 1, varför v_f = c₀, vilket är en generell egenskap hos den förlustfria parledningen.

    Om det ledningen omgivande isolermaterialet (μ_r ≈ 1, ε_r > 1) inte är vakuum (luft) blir tydligen v_f < c₀.

    I ett generellt fall med förluster blir α, β och v_f mer eller mindre komplicerade funktioner av frekvensen. Om exempelvis ωl << r och g << ωc får vi

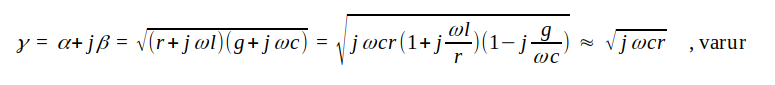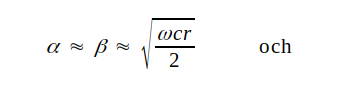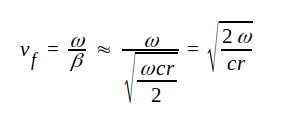J1.39

    I detta fall blir fashastigheten frekvensberoende. Dispersion säges då föreligga. Dispersion innebär, att vågor av olika frekvens, som från närändan startar i ett visst inbördes fasläge, anländer till fjärrändan i ett annat fasläge. Dispersion kan därför leda till distorsion. I det studerade fallet får vi även distorsion på grund av dämpningskonstantens frekvensberoende. Vågor med olika frekvens dämpas olika mycket.

    Om r << ωl och ωc << g erhålles

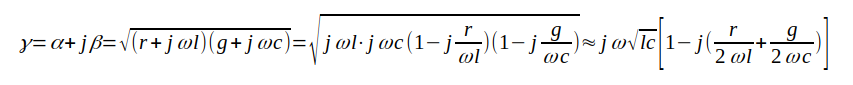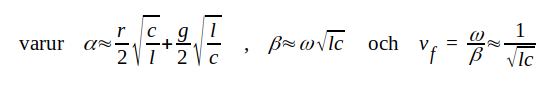J1.40

    I detta fall föreligger ej dispersion och vidare är α frekvensoberoende, varför ledningen är approximativt distorsionsfri (under förutsättning att r, l, g och c är frekvensoberoende).

Övning: Visa att Heaviside's ideala ledning är distorsionsfri.


link >