< link link link >

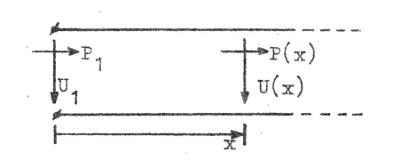
		Låt oss åter studera en oändligt lång (eller med Z0 avslutad) ledning enligt fig. J1.8, där P1 = på ledningen inmatad effekt och där P(x) = den effekt som passerar planet x.     Vi har
Fig. J1.8

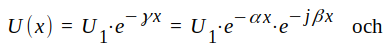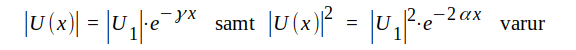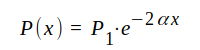J1.41

    J1.41 följer av det förhållande, att effekterna är proportionella mot respektive spänningars effektivvärderskvadrater, om spänningarna arbeta på samma impedans. I detta fall känner U1 och U(x) en och samma impedans Z₀. Ur J1.41 fås

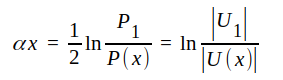J1.42

    Talet αx benämnes dämpningen och uttryckes i neper som enhet. α är sålunda dämpningen per längdenhet ledning (neper/meter). J1.42 anvisar en möjlig metod för bestämmning av dämpkonstanten α: på en anpassad ledning mäter man spänningen i två på känt avstånd från varandra belägna plan, varefter α kan beräknas ur J1.42.

    Deriveras J1.41 med avseende på x erhålles

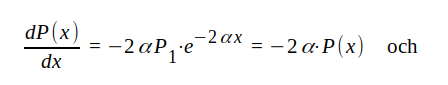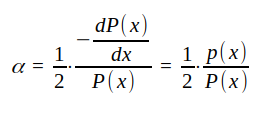J1.43

där 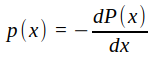 = förlusteffekt per längdenhet.

    Vi har därmed för α fått en definitionsekvation, som vi i vissa kommande sammanhang kan få användning av.

Övning: En ledning antages ha givet r och g, medan l och c kan väljas godtyckligt.  r << ωl och g << ωc. Visa att dämpningskonstanten får ett minimum, då r/g = l/c (Heaviside's ideala ledning).


link >