< link link link >

    Vi har hittills endast betraktat stationära sinusvågor på en ledning och vi har därvid infört begreppet fashastighet som en i dylika sammanhang lämplig storhet. Om den på ledningen inmatade spänningen är en signal (t.ex. en kortvarig spänningspuls, en intermittent utsänd sinusvåg eller en på annat sätt modulerad sinusvåg) frågar vi oss: med vilken hastighet fortskrider signalen (informationen) längs ledningen?

    Vi väljer att mata ledningens närända med en matematiskt sett relativt enkel signalspänning, nämligen

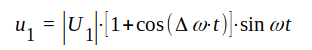J1.44

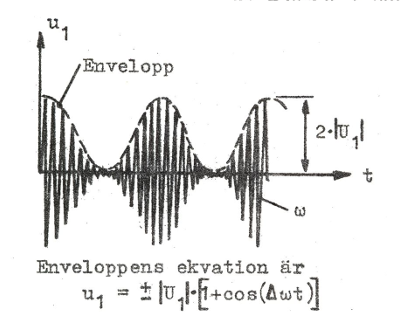
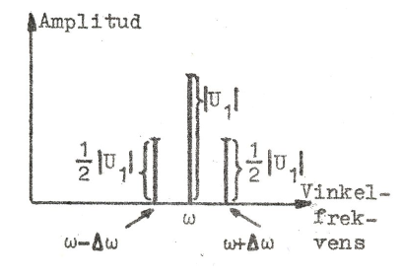
		u1, vars oscillogram framgår av fig. J1.9, är en typisk radiosignal (en till 100% med sinusspänning  modulerad bärvåg med bärvinkelfrekvensen ω och Δω signalfrekvensen ), vars information representeras av radiosignalens envelopp. Frågeställningen är nu:  med vilken hastighet fortskrider enveloppen på ledningen?
Fig. J1.9

    Vi antager, att Δω << ω. Ledningens faskonstant beror av frekvensen och vi antager därför att faskonstanten är β±Δβ, då vinkelfrekvensen är ω±Δω. Slutligen förutsätter vi för enkelhets skull, att dämpningskonstanten α = 0.

    Med hjälp av kända trigonometriska formler kan J1.44 omformas på följande sätt.

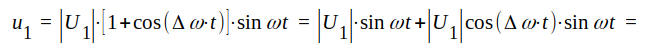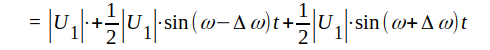J1.45

		Radiosignalen utgöres alltså av tre sinusspänningar med något olika frekvens (bärvåg + undre och övre sidvåg), och har ett spektrogram enligt fig. J1.10. I ett plan på avståndet x  från ledningens närända har de tre spänningarna undergått viss fasvridning och med hänsyn till våra antaganden får vi därför i planet x spänningen
Fig. J1.10

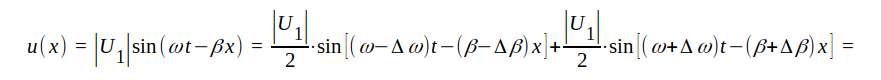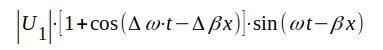J1.46

    Faktorn  är tydligen vågens envelopp. Om vi önskar röra oss framåt längs ledningen i takt med en fixerad punkt på den fortskridande enveloppen, måste vi förflytta oss så, att


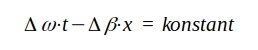    Derivering ger


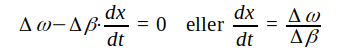    Vi definierar grupphastigheten  v_g som

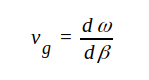J1.47

    Grupphastigheten v_g är enligt ovan den hastighet, varmed ett (oändligt smalt) frekvensband förflyttar sig längs ledningen. Grupphastigheten är alltid mindre än eller högst lika med ljushastigheten. Vårt resultat har en mera allmän innebörd, eftersom alla pulser kan betraktas som våginterferenser. Om ledningen har längden s, definierar vi löptiden t_g som

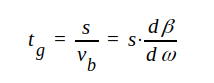J1.48

    I allmänhet är 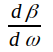 ej oberoende av frekvensen, varför löptiden blir olika för olika frekvenser. Man brukar dock definiera löptiden enligt ovan vid den frekvens, där signalens största effekt befinner sig.

    För en förlustfri ledning (och även för Heaviside's ideala ledning) gäller, att

, varför vi får

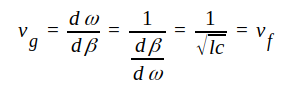J1.49

    För en förlustfri ledning är sålunda fashastigheten och grupphastigheten lika. Om dielektrikum är luft är dessutom båda lika med 3·10⁸ m/s.

    För en ledning (telefonkabel) med ωl <<r och g << ωc gäller (se sid, J1.12) att

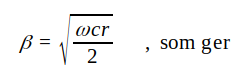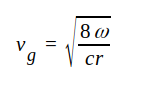J1.50

d.v.s vi får i detta fall en frekvensberoende grupphastighet.


link >