För att vi ur sambanden J1.13 och J1.14 (sid. J1.5) skall kunna beräkna spänning och ström i ett godtyckligt plan x på ledningen måste vi bestämma de två konstanterna U+ och U-. Härför erfordras två villkor. Exempelvis kan spänning och ström i ledningens närända eller motsvarande storheter i fjärrändan vara kända. Vi kan också, vilket kanske är det vanligaste, känna spänningen i närändan samt belastningsimpedansen Z2.
| |
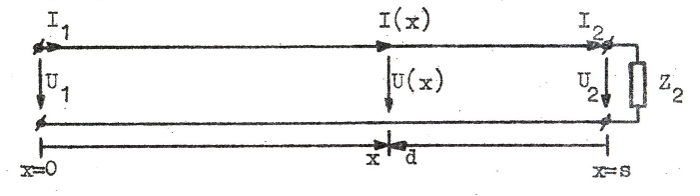 x + d = s x + d = s |
|
| |
Fig. J1.11 |
|
Vi antager till en början, att vi känner U1 och I1. Enligt J1.13 har vi
 |
J1.51 |
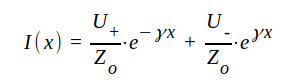 |
J1.52 |
Sätter vi i dessa ekvationer x = 0 erhålles
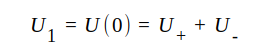 |
J1.53 |
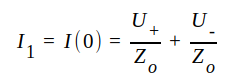 |
J1.54 |
Detta ekvationssystem ger
 |
J1.55 och J1.56 |
Insättning av J1.55 och J1.56 ger
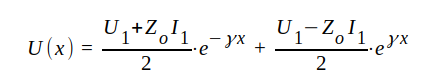 |
J1.57 |
Som tidigare konstaterat betyder första termen i J1.57 en framgående våg och andra termen en återgående våg. Totala spänningen U(x) på ledningen sammansätter sig sålunda av fram- och återgående våg. Vid anpassad ledning (Z2 = Z0) blir, som vi tidigare sett, även Z1 = U1 / I1 = Z0 och sista termen i J1.57 blir därför noll i detta fall. Den återgående vågen uppstår sålunda endast, om ledningen är missanpassad ( Z2 ≠ Z0). Vid missanpassning får vi därför tänka oss, att en del av den framgående vågen "reflekteras" vid belastningen. Den återgående vågen benämner vi därför i fortsättningen ofta reflekterad våg.
J1.57 kan bringas i en för praktisk räkning mera lämplig form.
Vi skriver om J1.57 på följande sätt
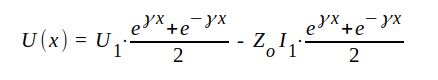 |
|
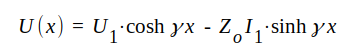 |
J1.58 |
Insättning av J1.55 och J1.56 i J1.52 ger på liknande sätt
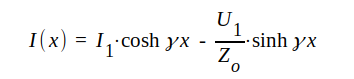 |
J1.59 |
För att få något enklare beteckningar inför vi i fortsättningen Ux ≌ U(x) och Ix ≌ I(x). Vi sammanfattar (läsaren verifierar riktigheten av J1.62 och J1.63):
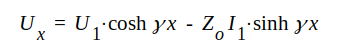 |
J1.60 |
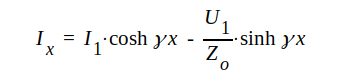 |
J1.61 |
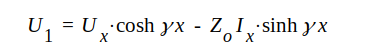 |
J1.62 |
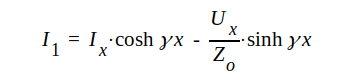 |
J1.63 |
Sätter vi i J1.60-J1.63 x = s blir Ux = U2 och Ix = I2. Vi får då sambanden mellan ledningens in- och utstorheter.
Med ledning av sambanden J1.60-J1.63 torde det utan vidare vara klart, att vi även kan skriva
| J1.64 |
|
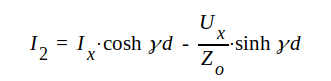 |
J1.65 |
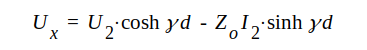 |
J1.66 |
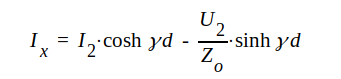 |
J1.67 |
Ekvationerna J1.60-J1.67 sammanfattar vi under beteckningen ledningens fyrpolsekvationer.
Om ledningen är förlustfri (r=0, g=0) är a = 0, d.v.s. vi får
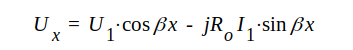 |
J1.68 |
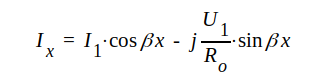 |
J1.69 |
Övriga ekvationer J1.62 - J1.67 förenklas i det förlustfria fallet på motsvarande sätt. Inledningsvis antogs U1 och I1 vara givna storheter. Sedan vi nu härlett fyrpolsekvationerna är det givetvis likgiltigt vilka två storheter vi anser vara givna.
För att man ej i varje särskilt problem skall behöva bestämma de i den ursprungliga lösningen ingående konstanterna U+ och U- bör ekvationerna J1.60 - J1.67 lämpligen inläras och ihågkommas.
link >