Vi utgår från ekvationerna J1.62 och J1.63 samt sätter x = s.
Vi har alltså
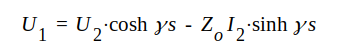 |
J1.70 |
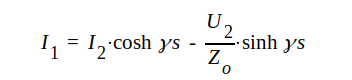 |
J1.71 |
Fall I: Ledningen kortsluten i fjärrändan.
| |
 |
|
| |
Fig. J1.12 |
|
U2 = 0 på grund av kortslutningen. J1.70 och J1.71 ger därför
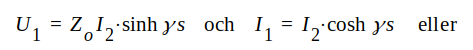 |
|
 |
J1.72 |
Zk är tydligen den impedans, vi känner mellan ledningens ingångsklämmor, då ledningen är kortsluten i fjärrändan. Zk benämner vi ledningens komplexa kortslutningsimpedans. Vi har
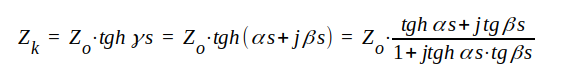 |
J1.73 |
och
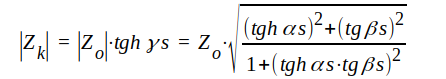 |
J1.74 |
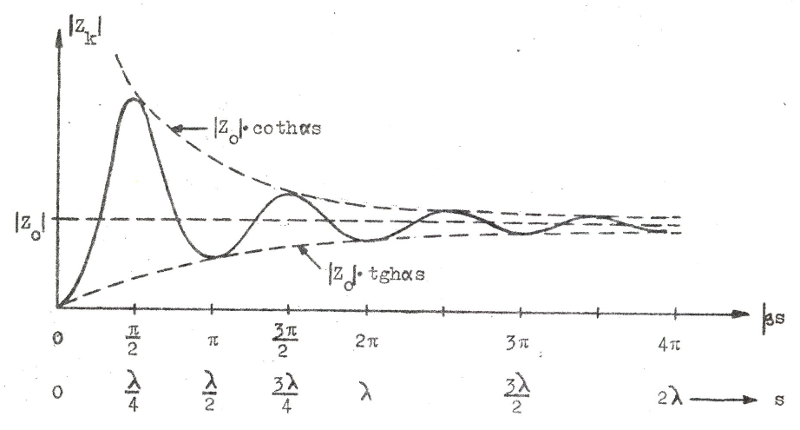
Ritar vi ∣Zk∣ som funktion av βs (ledningens elektriska längd) eller s (här lämpligen uttryckt i våglängder) fås följande fig. J1.13
| |
 |
|
| |
Fig. J1.13 |
|
Lägg märke till att vi får impedansminima för
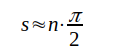 (n = 0, 1, 2, 3 ....) och
impedansmaxima för
(n = 0, 1, 2, 3 ....) och
impedansmaxima för 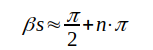 d.v.s. för
d.v.s. för 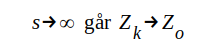 . Varje praktisk ledning, vars
längd överskrider ett visst minimum, får ingångsimpedansen Z0,
oberoende av fjärrändans belastning. Den framgående vågen har
nämligen i ett dylikt fall dämpats ut till noll, innan den når
belastningen eller har i varje fall dämpats ut till noll, innan
den når belastningen eller har i varje fall en eventuellt
reflekterad våg helt dämpats ut, innan den når närändan. Vid
närändan finnes alltså endast en framgående våg, varför
ingångsimpedansen måste bli lika med egenimpedansen.
. Varje praktisk ledning, vars
längd överskrider ett visst minimum, får ingångsimpedansen Z0,
oberoende av fjärrändans belastning. Den framgående vågen har
nämligen i ett dylikt fall dämpats ut till noll, innan den når
belastningen eller har i varje fall dämpats ut till noll, innan
den når belastningen eller har i varje fall en eventuellt
reflekterad våg helt dämpats ut, innan den når närändan. Vid
närändan finnes alltså endast en framgående våg, varför
ingångsimpedansen måste bli lika med egenimpedansen.Är ledningen förlustfri är γ = jβ och Z0 = R0. Eftersom tgh(jβs) = j ⋅ tgβs erhålles i detta fall ur J1.72
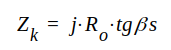 |
J1.75 |
I det förlustfria fallet är kortslutningsimpedansen en ren reaktans. Vidare blir Zk = 0, om
 (n = 0, 1, 2, 3 ....), och ,
(n = 0, 1, 2, 3 ....), och , 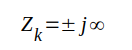 om
om Övning: Rita motsvarigheten till fig. J1.13 i det förlustfria fallet.
Fall II: Ledningen öppen i fjärrändan.
| |
 |
|
| |
Fig. J1.14 |
|
I detta fall måste I2 = 0 och vi får ur J1.70 och J1.71
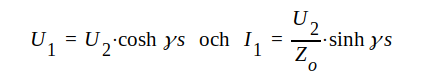 , vilka ger , vilka ger |
|
 |
J1.76 |
Zt benämner vi ledningens komplexa tomgångsimpedans.
Är ledningen förlustfri får vi
| J1.77 |
I fallet förlustfri ledning är sålunda tomgångsimpedansen en ren reaktans och vi får Zt = ∞, om
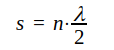 , samt Zt = 0, om
, samt Zt = 0, om 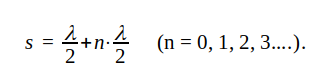 .
.Övning: Rita med ledning av J1.76 ∣Zt∣ som funktion av βs (eller s).
Av J1.72 och J1.76 följer, att
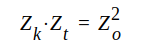 |
J1.78 |
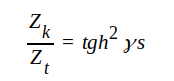 |
J1.79 |
En praktisk mätmetod för bestämning av ledningens såväl sekundära som primära konstanter anvisas av J1.78 och J1.79. Uppmätes nämligen Zk och Zt för en ledning med känd längd, kan tydligen γ (och därmed α och β) och Z0 beräknas, varefter de primära konstanterna kan beräknas ur de sekundära.
Fall III: Ledningen i fjärrändan belastad med den godtyckliga belastningsimpedansen Z2. Detta är det generella fallet, som även inkluderar fall I och II ovan.
| |
 |
|
| |
Fig. J1.15 |
|
J1.70 och J1.71 ger i detta fall
 |
som efter division med I2 ∙ coshγs i täljare och nämnare ger
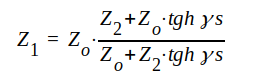 |
J1.80 |
som alltså är det generella uttrycket för ingångsimpedansen.
Läsaren kontrollerar själv genom insättning i J1.80, att
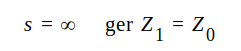 |
|
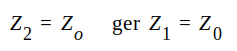 |
|
 |
Är ledningen förlustfri, får J1.80 formen
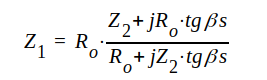 |
J1.81 |
Uttrycket för ingångsadmittansen blir i det generella fallet
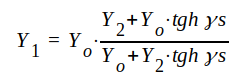 |
J1.82 |
där
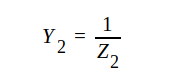 och
och 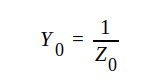 = ledningens komplexa
egenadmittans.
= ledningens komplexa
egenadmittans.link >