I det föregående har vi berört begreppet reflexion. Vi skall i detta avsnitt något närmare analysera detta begrepp och väljer att studera en ledning i fjärrändan belastad med den komplexa impedansen Z2 i enlighet med fig. J1.20.
| |
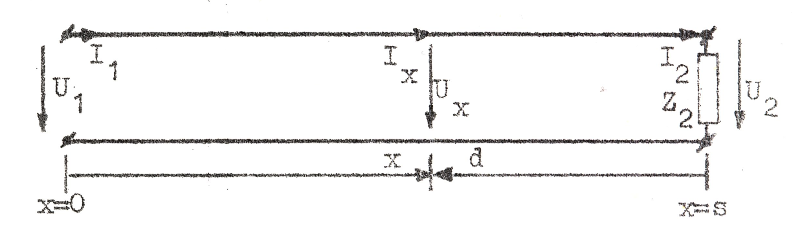 U2 = Z2 I2 U2 = Z2 I2 |
|
| |
Fig. J1.20 |
|
Enligt J1.66 och J1.67 gäller, att
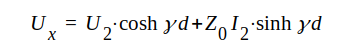 |
J1.90 |
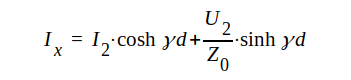 |
J1.91 |
Vi spaltar upp Ux i framgående och reflekterad våg genom att övergå från hyperboliska funktioner till exponentialfunktioner. Ur J1.90 erhålles
Vi bryter ut I2 och får, eftersom U2 = Z2 I2
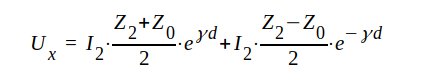 |
J1.92 |
Observera, att eγd-termen representerar den framgående vågen, då ledningsvariabeln är d. Detta framgår kanske enklast av att e-γd-termen blir noll, då ledningen är anpassad, d.v.s. Z2 = Z0.
Vi inför UF och UR som beteckning för komplex framgående spänningsvåg respektive komplex reflekterad spänningsvåg.
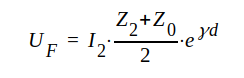 |
J1.93 |
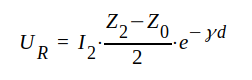 |
J1.94 |
Kvoten UR/UF i ett visst plan d betecknar vi ρud, som vi benämer komplexa reflexionsfaktorn för spänning i planet d. Vi har alltså
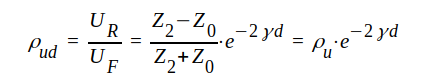 |
J1.95 |
där vi infört
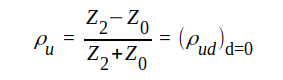 |
J1.96 |
ρu är alltså komplexa reflextionsfaktorn för spänning vid belastningen.
Slutligen sätter vi
 |
J1.97 |
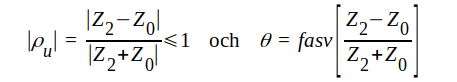 |
J1.98 |
Om ekvation J1.91 spaltas upp i framgående och reflekterad våg i analogi med räkningen ovan, finner man, att
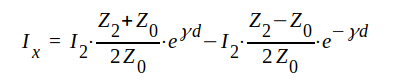 |
J1.99 |
eller, som väntat
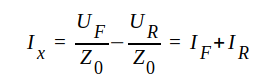 |
J1.100 |
där IF = UF/Z0 = komplex framgående strömvåg och
IR = -UR/Z0 = komplex reflekterad strömvåg.
Vi definierar komplexa reflexionsfaktorn för ström i planet d som
 |
J1.101 |
Vidare är
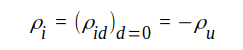 |
J1.102 |
ρi är komplexa reflexionsfaktorn för ström vid belastningen.
Man observerar speciellt följande fyra fall, nämligen
| a) ρu = 0 och ρi = 0 för Z2 = Z0 | |
| b) ρu = -1 och ρi =
+1 för Z2 = 0 |
|
| c) ρu = +1 och ρi =
-1 för Z2 = ∞ |
|
| d) ∣ρu∣ = 1 och ∣ρi∣
= 1 för Z2 = jX2 |
I fall a är ρu = ρi = 0, vilket innebär, att vi ej har någon reflekterad våg, något som vi redan konstaterat i annat sammanhang.
I fallen b, c och d är ∣ρu∣ = ∣ρi∣ = 1, d.v.s. framgående och reflekterad våg har vid belastningen samma såväl spännings- som strömamplitud, vilket bör vara självklart, eftersom ingen effekt förbrukas i belastningen i dessa fall; den framgående vågens effekt måste återföras av den återgående vågen
Att i fallet b (kortsluten fjärrända) ρu = -1 betyder, att den reflekterade spänningsvågen vid belastningen ligger 180° ur fas med den framgående, vilket är nödvändigt, eftersom summaspänningen (spänningen över kortslutningen) skall vara noll. Att ρi = +1 i detta fall kan vi även förstå, eftersom en fasomkastning (180°) av såväl spänning som ström ej skulle ändrat den mot kortslutningen infallande vågens gångriktning. Total strömamplitud genom kortslutningen blir sålunda dubbelt så stor som den framgående vågens strömamplitud vid kortslutningen.
Övning: Tänk igenom fallet c på analogt sätt
I fall d slutligen blir ∣ρu∣ = ∣ρi∣ = 1, eftersom ingen effekt förbrukas i belastningen. Däremot introducerar reaktansen X2 en fasvridning mellan fram- och återgående våg.
link >