< link link link >

    I avsikt att få ytterligare insyn i reflextionsförhållandena på en ledning studerar vi en förlustfri ledning, som i fjärrändan är kortsluten. Vi väljer godtyckligt ledningens längd till .

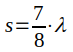Om vi antager, att I₂ = │I₂│⋅ e^jωt, fås i detta fall (γ = jβ,  Z₀ = R₀ och Z₂ = 0) ur J1.93, J1.94 och J1.100

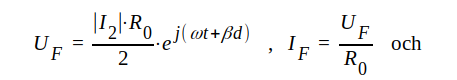	J1.103
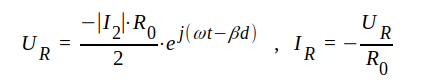	J1.104

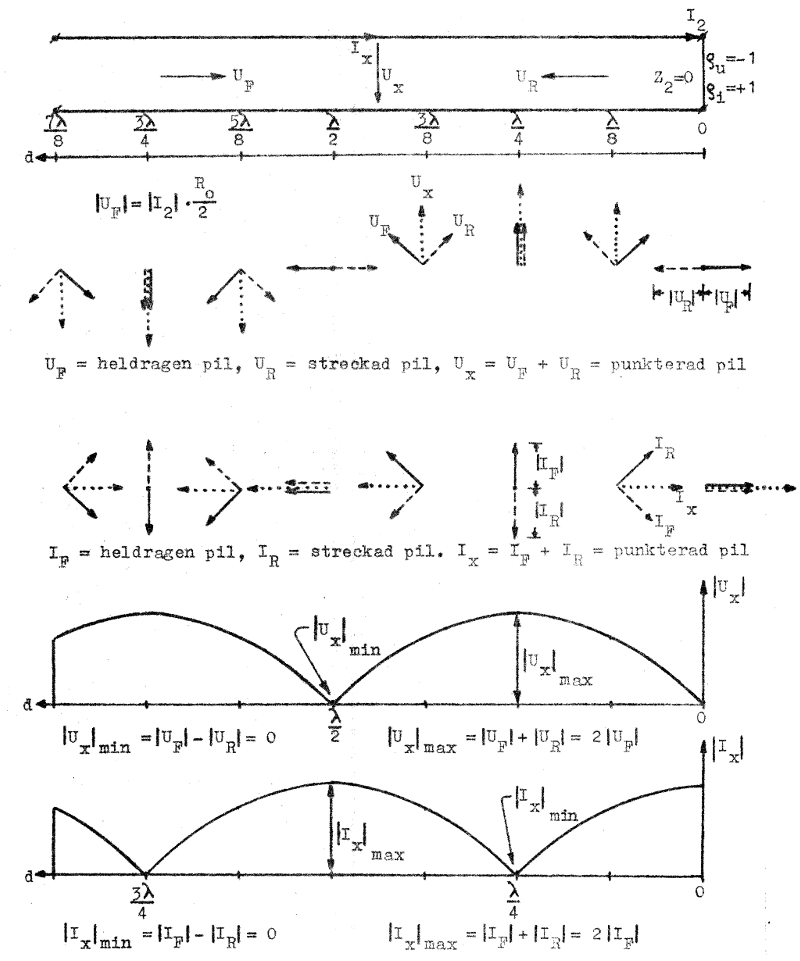
    Låt oss nu för en fix tid t (vi väljer för enkelhets skull t=0) rita U_F och U_R respektive I_F och I_R i komplexa talplanet för en seire olika d-värden (d = 0, λ/8, λ/4, 3λ/8......7λ/8). Vi ritar först U_F-visaren i ledningens närända, d.v.s. för d = 7λ/8, som ger


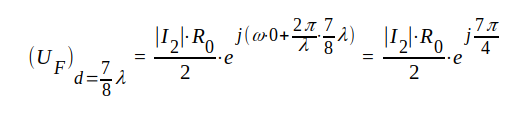     För varje åttondels våglängd, som vi går i riktning mot belastningen (kortslutningen), vrides spänningsvisaren 45° medsols, medan amplituden alltid är konstant (förlustfri ledning). Vi kan därför lätt rita samtliga U_F-visare. När vi kommer till kortslutningen kan vi rita U_R-visaren där, eftersom ρ_u = -1, d.v.s. U_R-visaren blir omkastad i förhållande till U_F-visaren. Övriga U_R-visare kan därefter ritas återigen genom vridning 45° för varje åttondels våglängd.

    Samma förfarande upprepas med I_F- och I_R-visarna. Vi får så de båda "visardiagrammen" i fig. J1.21 nedan.

    För varje d-värde kan nu U_x bestämmas som resultanten till U_R- och U_F-visaren, varefter slutligen U_x kan ritas som funktion av d. U_x är den spänning, som vi med växelspänningsinstrument kan mäta på ledningen. På liknande sätt kan I_x bestämmas och vi får på angivet sätt de båda nedersta diagrammen i fig. J1.21.

	Fig. J1.21

    Det matematiska uttrycket för U_x i detta fall (kortslutningsfallet, Z₂ = 0) härledes lätt ur J1.103 och J1.104. Vi får

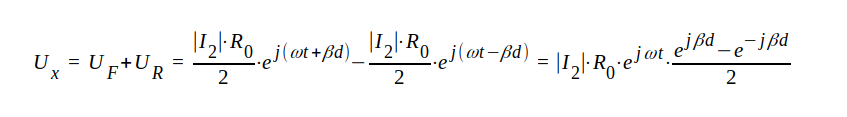J1.105

varur

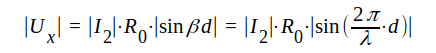J1.106

    J1.106 står helt i överensstämmelse med fig. J1.21. Sålunda framgår, att │U_x│ = 0 för sss (n = 0, 1, 2, 3, ......) och │U_x│-fördelningen längs ledningen är sinushalvor.

    Om i₂ = Im(I₂) = │I₂│ ⋅ sinωt, får ur J1.105 ögonblicksvärdet

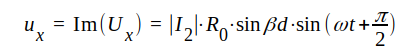J1.107

    I de tidsögonblick som har (n = 0, 1, 2, 3, ......) är momentanvärdet av spänningen överallt på ledningen lika med noll.

Övning: Rita u_x-fördelningen längs ledningen för

Övning: Härled i analogi med räkningarna ovan det matematiska uttrycket för I_x, │I_x│ och i_x i kortslutningsfallet.

Övning: Rita de mot fig. J1.21 svarande diagrammen, om ledningen är öppen i fjärrändan (Z₂ = ∞).

    Låt oss till sist studera ytterligare ett fall. Vi väljer åter en förlustfri ledning (sss som i föregående fall) resistivt belastad med Z₂ = 3R₀, d.v.s. vi har


    Om vi antar, att I₂ = │I₂│ ⋅ e^jωt fås i detta fall (γ = jβ; Z₀ = R₀; Z₂ = 3R₀) ur sambanden J1.93. J1.94 och J1.100

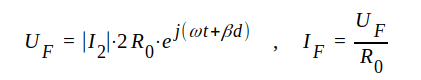	J1.108
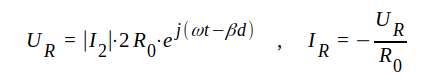	J1.109

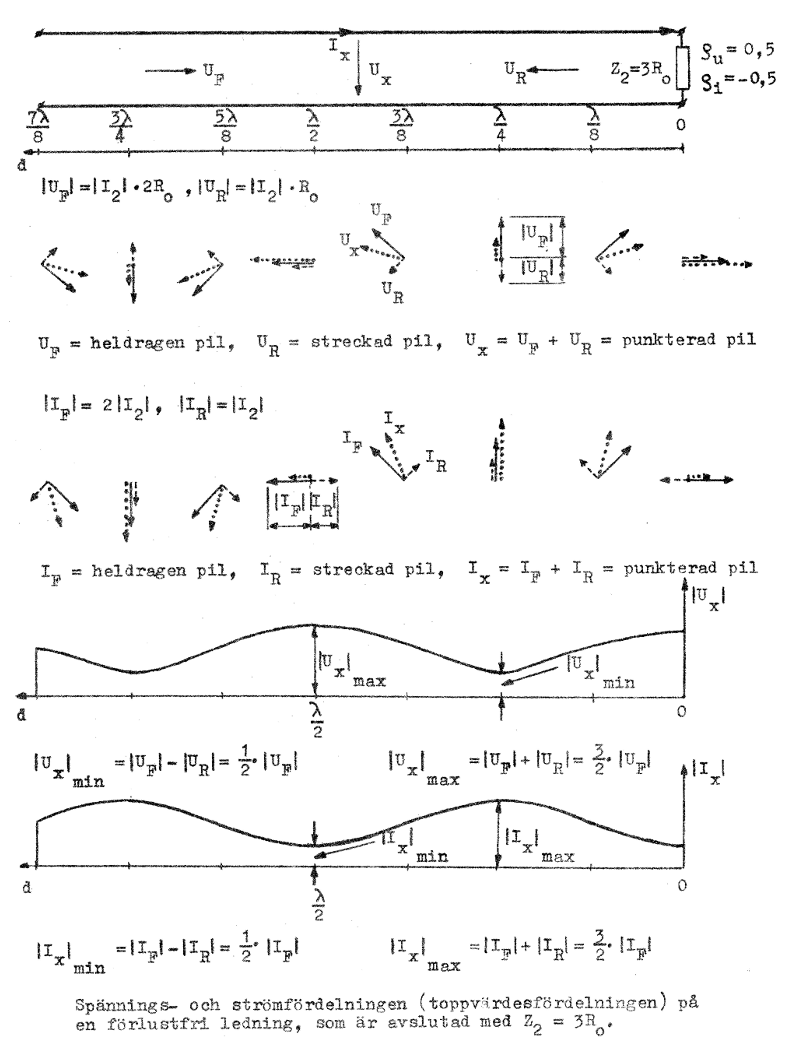
    Med ledning av dessa ekvationer kontrollerar läsaren på egen hand och i analogi med föregående fall (se texten efter ekvation J1.104) riktigheten hos följande figursystem (fig. J1.22).

	Fig. J1.22

Läsaren visar lämpligen på egen hand att det matematiska uttrycket för │U_x│-fördelningen på ledningen är

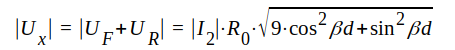J1.110

    Vi observerar sålunda, att fördelningskurvorna i fig. J1.22 icke är sinusformade.

    Av våra exempel framgår att till fixa d-värden bundna amplitudmaxima (spänningsbukar, strömbukar) och likaledes till fixa d-värden bundna amplitudminima (spänningsnoder, strömnoder) har uppstått på ledningen. Vi säger, att en stående vå utbildats på ledningen (jämför den svängande strägen, vars avvikelse från jämviktsläget motsvarar spänningens momentanvärde i det ovan behandlade kortslutningsfallet). Har vi på ledningen endast framgående våg (anpassad ledning) är U_x = U_F och I_x = I_F, d.v.s. amplituden är överallt konstant och vi har ingen stående våg. Har ledningen förluster, faller amplituden i detta fall i riktningen mot belastningen, men någon stående våg finns givetvis ej heller i detta fall

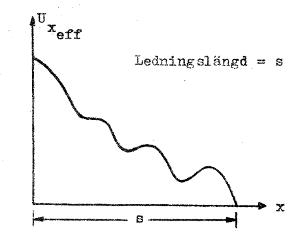
Övning: Man har uppmätt effektivvärdesfördelningen hos en spänningen på en viss ledning och därvid erhållit ett resultat i enlighet med vidstående figur. Besvara följande frågor: Hur lång var ledningen (i våglängder räknat)? Var ledningen förlustfri? Hur stor var belastningsimpedansen? Hur stor är approximativt ledningens ingångsimpedans?
		Fig. J1.23

    Vi sammanfattar nedan några stående-våg-egenskaper, som vi funnit vid studium av de två förlustfria fallen ovan.

1. Avståndet mellan två närliggande noder (bukar) är en halv våglängd
2. Spänningsnoder och strömbukar (respektive spänningsbukar och strömnoder) inträffar på samma ställe på ledningen.
3. I en spänningsbuk ligger framgående och reflekterad spänningsvåg i fas med varandra. Samma gäller strömvågorna i strömbuken.
4. I en spänningsnod ligger framgående och reflekterad spänningsvåg i motfas. Samma gäller strömvågorna i strömnoden.
5. I såväl bukar som i noder ligger total spänning (U_x) och total ström i fas med varandra, vilket innebär, att ledningens impedans är resistiv i bukar och noder.

Övning: Är impedansen störst i en spänningsbuk eller i en spänningsnod?

    I vårt senaste studerade exempel (fig. J1.22) observerar vi, att │U_x│_min ≠ 0 och vi introducerar nu begreppet stående-våg-förhållande, ofta förkortat med SVF, genom definitionen:

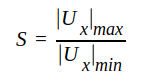J1.111

    SVF, som vi betecknar med S, är tydligen ett positivt tal, som kan anta alla värden mellan 1 (ingen reflexion, anpassning) och ∞ (total reflexion vid belastningen).

Övning: Hur stort är SVF i fig. J1.21 respektive i fig. J1.22?

link >