< link link link >

    Begreppet stående-våg-förhållande (SVF), som berörts i föregående avsnitt, är av väsentlig betydelse i fråga om förlustfria ledningar (närmelsevis förlustfria ledningar; radiofrekvensledningar). För ytterligare studium av nämnda begrepp utgår vi från ekvation J1.92, som i det förlustfria fallet (γ = jβ, Z₀ = R₀) lyder

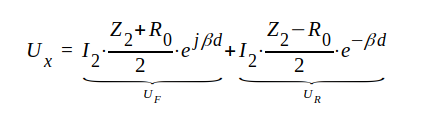J1.112

där U_F och U_R liksom tidigare betecknar komplex spänning i fram respektive återgående (reflekterad) våg.

    Eftersom I_F = U_F / R₀ och I_R = -U_R/R₀ får vi sammanfattningsvis och med ledning av sambanden J1.96, J1.97 och J1.98:

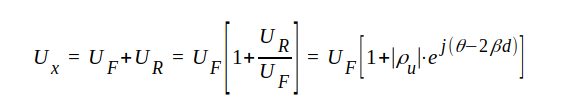	J1.113
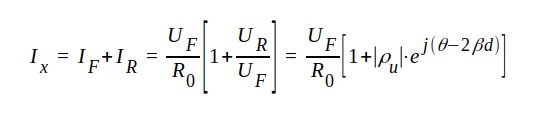	J1.114

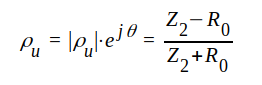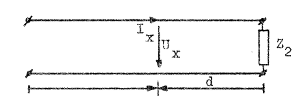
	Fig. J1.24	.

     Rör vi oss längs ledningen (d i fig. J1.24 varieras), så ändrar sig spännings- och strömamplitud enligt följande samband, som erhålles direkt ur sambanden J1.113 och J1.114.

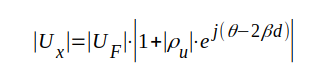	J1.115
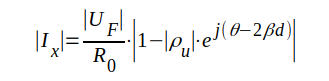	J1.116

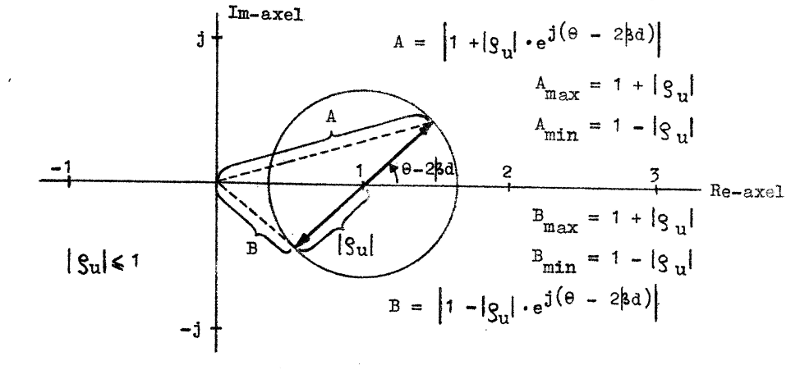
    Hur ∣U_x∣ och ∣I_x∣ varierar, då vi ändrar d vid i övrigt oförändrade förhållanden, framgår av nedanstående konstruktion i komplexa talplanet.
Figuren är ritad med ledning av sambanden J1.115 och J1.116.

	Fig. J1.25

    Spänningsamplituden ∣U_x∣ är tydligen proportionell mot sträckan A i fig. J1.25 medan strömamplituden ∣I_x∣ är proportionell mot sträckan B. Då sträckan A vid ett visst värde på d är maximal (A_max) är sträckan B samtidigt minimal (B_min) och vice versa, innebärande att spänningsmaximum (spänningsbuk) alltid inträffar på samma ställe på ledningen som strömminimum (strömnod). Samma gäller för spänningsminimum och strömmaximum.
Vi har alltså

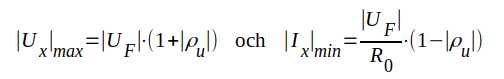J1.117a

då θ - 2βd = ± n·2π, n = 0, 1, 2 ... , d.v.s. spänningsmaximum då

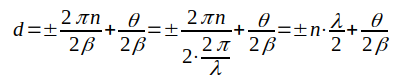J1.117b

    På analogt sätt får vi

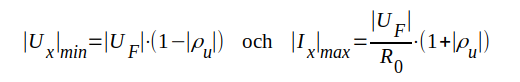J1.118a

då θ - 2βd = ± (2m +1)π, m = 0, 1, 2 ... , d.v.s. spänningsminimum då

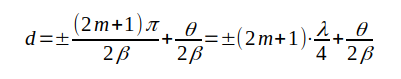J1.118b

Tecknet i sambandet J1.117b och i sambandet J1.118b måste givetvis väljas så, att storheten d blir positiv.

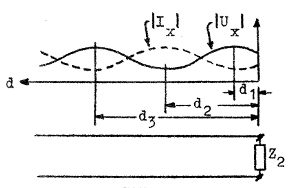
För ett tänkt fall med poitivt θ-värde enligt fig. J1.26 inträffar det första spänningsmaximet (det, som befinner sig närmast belastningen Z2) på avståndet d1 från belastningen.
		Fig. J1.26

    Vi har


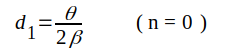    Närmaste minimum i spänning inträffar på avståndet d2 från belastningen och vi har


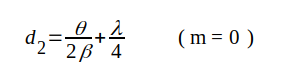    Det därpå följande spänningsmaximet inträffar vid d3, där


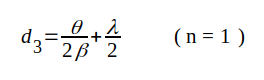    Av ovanstående följer att


    Vi konstaterar med andra ord åter några av de egenskaper, som vi redan tidigare funnit (se nederst sid. J1.30).

    Med ledning av sambanden J1.117a och J1.118a kan vi nu beräkna ett uttryck på stående-våg-förhållandet S. Vi får

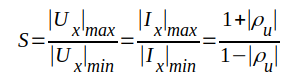	J1.119
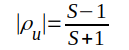	J1.120

    d.v.s mätning av S (vilket relativt lätt kan utföras på ledningar för hög frekvens) ger direkt komplexa reflextionsfaktorns absolutbelopp, något som pekar hän mot en mätmetodik för bestämning av belastningsimpedansen Z₂, nämligen på följande sätt.

Mätmetodik:

1. Mät SVF och beräkna ∣ρ_u∣ ur sambandet J1.120
2. Mät avståndet (λ/2) mellan två på varandra följande spänningsminima (maxima) och beräkna våglängden λ
3. Mät avståndet mellan belastningen och ett spänningsminimum eller spänningsmaximum (t.ex. d1 i fig J1.26). Beräkna ρ_u:s fasvinkel θ ( i exemplet ovan får vi θ = 2βd₁ = 4πd₁/λ).
4. Beräkna komplexa belastningsimpedansen Z₂ ur sambandet J1.96, som lyder

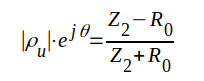J1.121

Beräkningen förutsätter, att vi känner eller har bestämt egenimpedansen (egenresistansen) R₀. I många fall är man endast intresserad av kvoten Z₂/R₀, som kan beräknas ur sambandet J1.121 utan kännedom om R₀.

    Den beskrivna mätmetodiken är av synnerlig vikt vid ledningar för extremt hög frekvens (vågledare). För bestämning av S och för bestämning av läget hos minima och maxima (våglängdsbestämning) användes därvid speciella s.k. stående-våg-mätare (se lab. nr 21).
Övning: Vid impedansbestämning med hjälp av stående-våg-meter uppmäter man S (SVF), d (avståndet mellan belastningen Z₂ och närmaste spänningsminimum) och λ (våglängden). Härled med utgångspunkt från sambandet J1.21 följande praktiska arbetsformel:

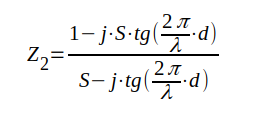J1.122

link >