Vi har tidigare definierat komplexa impedansen i planet x (planet d) för en ledning (se t.ex. fig J1.24) som
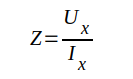 |
J1.123 |
Med hjälp av sambanden J1.113 och J1.114 får vi
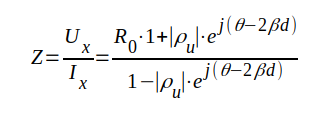 |
J1.124 |
I ett spänningsmaximum är θ - 2βd = ± n·2π (sid. J1.32), d.v.s. ej(θ - 2βd) = 1, varför
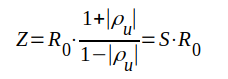 i
spänningsmaximum i
spänningsmaximum |
J1.125 |
På analogt sätt får vi i ett spänningsminimum
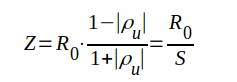 i
spänningsminimum i
spänningsminimum |
J1.126 |
Impedansen är sålunda resistiv i såväl spänningsmaximum som i spänningsminimum och den står i en mycket enkel relation till ledningens egenresistans R0.
Av sambanden J1.125 och J1.126 följer att spänningsmaximum inträffar vid belastningen, om denna är resistiv och större än egenresistansen R0. På samma sätt inträffar spänningsminimum vid belastningen, om denna är resistiv och mindre än egenresistansen R0 (jämför fig. J1.22, där Z2 = 3R0).
link >