< link link link >

    a) Kvartsvågstransformatorn

Vi har tidigare (se ekvation J1.81) beräknat den komplexa inimpedansen hos en förlustfri ledning med längden s och belastningen Z2:
		Fig. J1.31

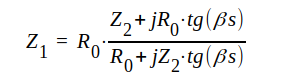J1.131

    Är  ledningslängden s = λ/4 (som i fig. J1.31) så blir


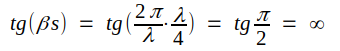och vi får

J1.132

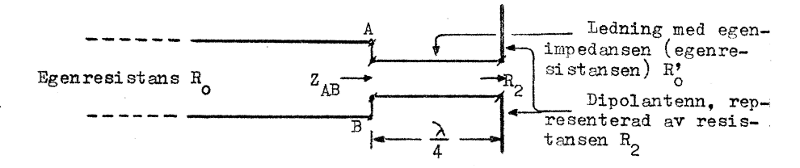
    Detta samband beskriver den s.k. kvartsvågstransformatorns princip, vars tillämpning vi demonstrerar på mycket vanligt fall: anpassning av en resistiv belastning (i fig. J1.32 en dipolantenn) R₂ till en transmissionsledning med den resistiva egenimpedansen R₀

	Fig. J1.32

    Skall huvudledningen vara anpassad måste den vara avslutad med R₀, d.v.s. Z_AB = R₀. Enligt sambandet J1.132 är emellertid


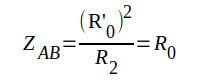    Kvartsvågsledningen måste alltså utföras så, att dess egenresistans blir

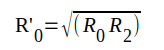J1.133

Övning: Skissera kvartsvågstransformatorns utförande dels i parledningsutförande och dels i koaxialutförande för de båda fallen R₂ > R₀ och R₂ < R₀.

    Om huvudledningen matas av en generator med inre resistansen R₀, torde det vara uppenbart

        dels att generatorn avger maximal effekt
        dels att all denna effekt förbrukas i belastningen R₂.

All från vänster mot klämmorna A-B infallande effekt passerar nämligen dessa klämmor, eftersom huvudledningen är reflexionsfritt avslutad (Z_AB = R₀). Till höger om klämmorna A-B kan effekten endast förbrukas i R₂, eftersom kvartsvågsledningen förutsatts förlustfri.

Övning: Har en förlustfri ledning med längden s = λ/8 några intressanta impedanstransformationsegenskaper? Ledning: Studera sambandet J1.131.

    b) Engrensanpassaren ("single-stub" anpassaren).

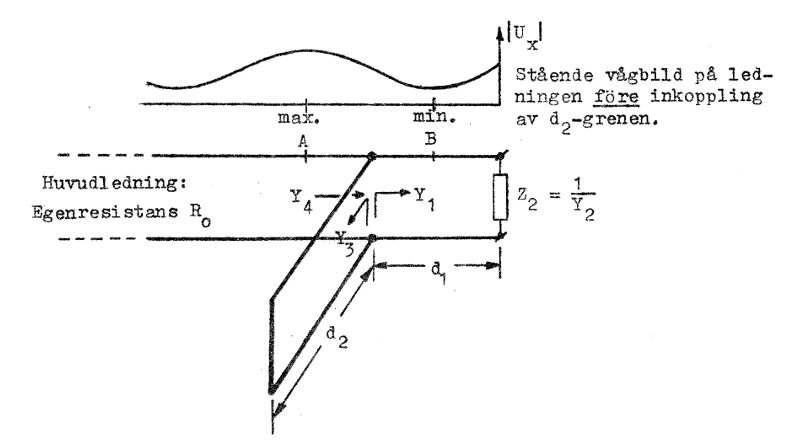
    En godtycklig belastning Z₂ kan anpassas till en ledning, om man på lämpligt avstånd d₁ (se fig. J1.33) från belastningen placerar en kortsluten (eller öppen) ledningsgren (reaktansgren) av lämplig längd d₂, något som vi kan inse på följande sätt:

	Engrensanpassarens princip. Fig. J1.33

    Antag att vi före inkopplingen av reaktansgrenen har en stående-våg-bild på ledningen i överensstämmelse med fig. J1.33 ovan (ett spänningsmaximum i A och ett spänningsminimum i B). Enligt sambanden J1.125 och J1.126 vet vi, att komplexa impedansen i ett spänningsmaximum respektive spänningsminimum är rent resistiv och lika med


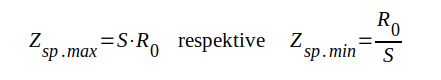    Vi arbetar här med parallellkopplade ledningsgrenar, vilket gör det fördelaktigt att räkna med admittanser i stället för impedanser. Vi inför därför


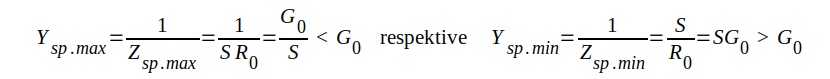där 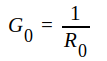 = ledningens egenkonduktans.

    Eftersom konduktansen varierar mellan S·G₀ ( >G₀) och G₀/S (<G₀), då vi förflyttar oss längs ledningen från ett spänningsminimum till ett spänningsmaximum, måste konduktansen någonstans mellan max. och min. punkterna anta värdet G₀. I denna punkt måste emellertid även finnas en viss suseptans B, eftersom max. och min. punkterna är de enda punkter, som har rent konduktiv admittans. På ett visst avstånd d1 från belastningen måste vi sålunda kunna finna en punkt, där komplexa admittansen antar värdet


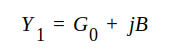    Placerar vi nu i punkten d₁ en kortsluten (eller öppen) ledningsgren (som ju är rent reaktiv) av sådan längd d₂ att dess inadmittans blir


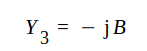så blir komplexa admittansen omedelbart till vänster om grenpunkten (se fig. J1.33)


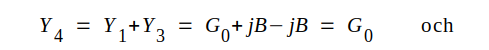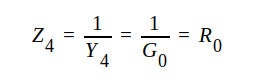    Huvudledningen är alltså anpassad och all effekt, som passerar grenpunkten, hamnar i belastningen Z₂, eftersom hela ledningssystemet till höger om grenpunkten förutsatts förlustfritt.

    Vi har därmed sett, att anpassning medelst engrensanpassare är möjlig. Beräkningen av längderna d1 och d2 genomförs lämpligen med grafiska metoder (Smith-diagram; se avsnitt J2) och förbigås därför här.

Övning: Visa att följande dimensioneringsformler gäller för en engrensanpassare med kortsluten reaktansgren.

	J1.134
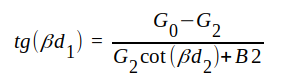	J1.135
där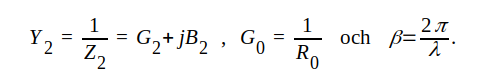

    c) Tvågrensanpassaren ("double-stub" anpassaren).

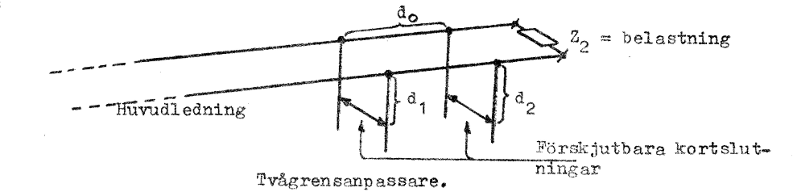
    Vid praktisk injustering av engrensanpassaren måste man justera längderna d₁ och d₂ (fig. J1.33), tills SVF på huvudledningen blir så nära ett som möjligt. Att variera reaktansgrens längd med hjälp av en förskjutbar kortslutning kan relativt lätt ordnas (även i koaxialledningensutförande). Att däremot variera längderna d₁ i koaxialledningsfallet ställer sig relativt besvärligt. Anpassning kan emellertid åstadkommas även med hjälp av två fasta reaktansgrenar på fast inbördes avstånd men med justerbara längder (d₁ och d₂ i fig. J1.34). Vi får då en s.k. tvågrensanpassare.

	Fig. J1.34

     Beräkning av längderna d₁ och d₂ (vid givet avstånd d₀) sker liksom i engrensfallet lättast med grafiska metoder och en på ledningsteorien baserad analytisk behandling förbigås därför här. Vi återkommer till tvågrensanpassaren i avsnitt J2. Det bör dock här nämnas, att en godtycklig impedans Z₂ ej med säkerhet kan anpassas med hjälp av en given tvågrensanpassare. Om anpassningsmöjlighet föreligger beror nämligen på avståndet d₀.

Övning: Är det lämpligt att göra avståndet d₀ lika med en halv våglängd?


link >