< link link link >

    En ledning med fix längd s₀ måste vid en viss frekvens f₀ vara en halv våglängd lång. Är ledningen förlustfri och dessutom kortsluten i fjärrändan, blir inimpedansen noll. Se härtill fig. J1.27 (sid. J1.36). Ökas frekvensen något från f₀-värdet, så minskas våglängden och ledningen blir därför elektriskt sett längre, varför inimpedansen blir induktiv (se åter fig. J1.27). Minskas frekvensen blir inimpedansen på analogt sätt kapacitiv. Sedd mellan sina ingångsklämmor beter sig ledningen som en förlustfri serieresonanskrets kring resonansfrekvensen f₀. Vi kan därför förmoda, att en kortsluten halvvåglängdssektion med förluster beter sig ungefär som en serieresonanskrets med förluster. Vi skall nedan undersöka denna fråga närmare.

Vi betraktar en i fjärrändan kortsluten icke förlustfri ledning med längden s0 (fig. J1.35). Vi antar, att ledningen är en halv våglängd lång vi frekvensen f0 (vinkelfrekvensen ω0), d.v.s.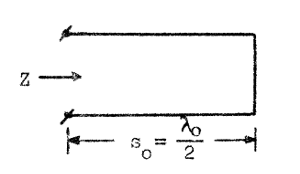
		Fig. J1.35

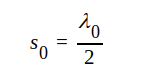där λ₀ är den mot frekvensen f₀ svarande våglängden. Den mot en godtycklig frekvens f (eller ω) svarande våglängden betecknar vi med λ.

    Komplexa kortslutningsimpedansen för en ledning med förluster är enligt sambandet J1.72:

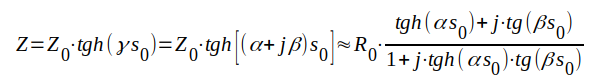J1.136

där vi utvecklat 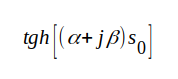 och där vi infört

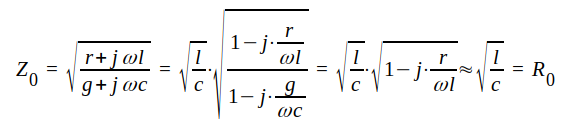J1.137

där vi satt g = 0 och antagit, att r << ωl, d.v.s. vi betraktar en ledning med mycket liten längdresistans r och helt försumbar tvärkonduktans g (luftledning, lecherledning, ledning med luft som isolator mellan de båda ledarna). Egenimpedansen hos en dylik närmelsevis förlustfri ledning kan vi alltså anse approximativt reell (resistiv).

    Om förlusterna är små, är det rimligt att förutsätta, att ∣Z∣ liksom i fråga om den förlustfria ledningen när sitt minimum, då βs₀ = π, d.v.s. då


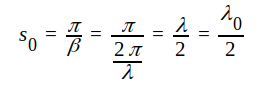d.v.s. då


    Vi kan skriva

J1.138

    För små avvikelser (Δω) från vinkelfrekvensen ω₀ är alltså

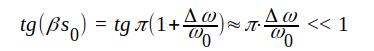J1.139

och på grund av små förluster (dämpningen αs₀ är liten) kan vi även sätta

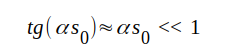J1.140

    I sambandet J1.136 kan vi i nämnaren vid små frekvensavvikelser Δω försumma termen tgh(αs₀)·tg(βs₀) i jämförelse med 1, speciellt med tanke på att termernas båda faktorer var och en för sig är avsevärt mindre än ett enligt våra diskussioner ovan. Vi kan alltså skriva sambandet J1.136 på följande sätt

J1.141

    Enligt sambanden J1.40 (sid. J1.12) gäller för en ledning med små förluster (och i detta fall g = 0) sambanden


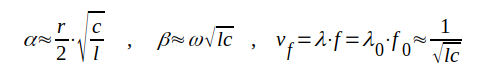    Insättning i sambandet J1.141 ger

J1.142

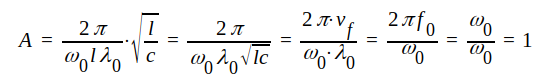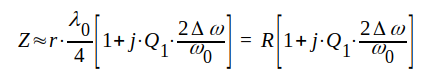J1.143

där vi infört  och 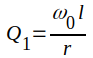 = halvvågssektionens egen-Q-värde.

    Sambandet J1.143 bör lämpligen jämföras med exempelvis sambandet B1.20 (del IB, sid. B1.8), något som visar, att sambandet J1.143 har samma form som impedansuttrycket för en serieresonanskrets i närheten av resonans.

    På analogt sätt kan man visa, att den ekvivalens, som framgår av nedanstående fig. J1.36 föreligger. Såväl slutna som öppna ledningssektioner kan alltså användas som resonanskretsar av både serie- och parallelltyp.

	Fig. J1.36

Övning: Visa att ovan definierade Q-värde kan skrivas

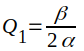
Övning: Härled ett uttryck för komplexa inimpedansen Z_CD i fig. J1.36 d.v.s. för fallet s₀ = λ₀/4. Det förutsätts, att r << ωl samt att g = 0. Gör lämpliga approximationer och bringa slutresultatet i sådan form, att jämförelse med parallellresonanskretsen kan göras.


link >