Detta kompendium behandlar det sinusformade stationära tillståndet på transmissionsledningar. Låt oss dock studera ett transient förlopp av tekniskt intresse, nämligen det, som skisserats i fig. J1.37.
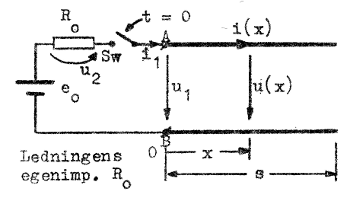 |
Ett batteri (emk: e0) i serie med resistansen R0 matar via brytaren Sw en förlustfri, i fjärrändan öppen ledning med egenimpedansen (egenresistansen) R0. Vi slår till brytaren Sw vid tidpunkten t = 0. Eftersom all utbredning på en ledning sker med ändlig hastighet, måste vi strax efter tillslag | |
| Fig. J1.37 |
endast ha en framgående våg på ledningen, d.v.s. u1/i1 = R0 eller med andra ord: inimpedansen mellan klämmorna A och B är R0 strax efter tillslag. Vi har alltså u1 = e0/2 efter tillslag och ända tills den i fjärrändan reflekterade vågen når inklämmorna A-B. Under samma tid är i1 = u1 / R0 = e0 / 2R0. Spänningsfronten e0/2 utbreder sig på ledningen och vi kan lätt rita spänningsfördelningen på ledningen vid olika tidpunkter t. Se härtill fig. J1.38, där T är vågformens löptid på ledningen.
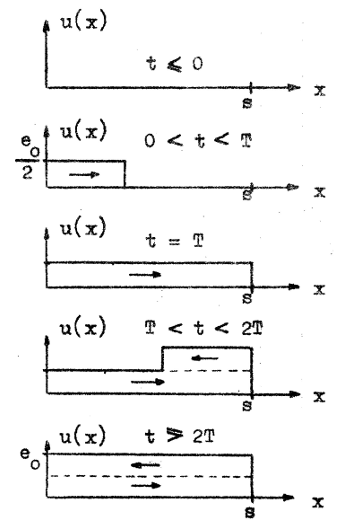 |
Tredje delfiguren ( T < t <
2T) förklaras av att reflektionsfaktorn ρu =
+1 (för strömmen har vi däremot ρu = -1). Av diagrammen framgår att 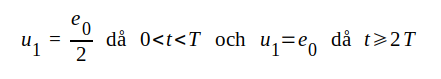 Läsaren konstaterar på egen hand att 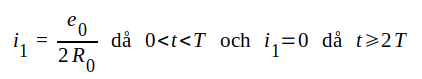 Spänningen över den yttre resistansen R0 blir tydligen en ideal rektangelpuls enligt fig. J1.39 nedan. 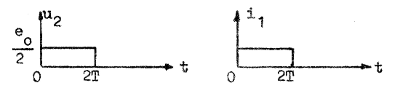 |
|
| Fig. J1.38 | Fig. J1.39 |
Övning: Rita den mot fig. J1.38 svarande strömdiagrammet.
Övning: Hur kommer fig. J1.39 att se ut, om den yttre resistansen är större respektive mindre än R0?
Övning: Hur lång ledning erfodras om man enligt metoden ovan önskar alstra en u2-puls med 1μs varaktighet?
Övning: Ledningen antages från början vara uppladdad till spänningen e0 och urladdas sedan via en yttre resistans R0. Hur ser strömpulsen genom yttre resistansen ut?
link >