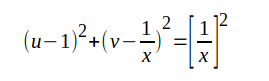För framtagning av det s.k. Smith-diagrammet utgår vi från sambandet J1.96 (sid. J1.25), d.v.s. uttrycket för komplexa reflexionsfaktorn ρu
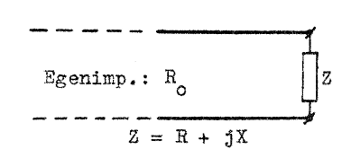 |
vid belastningen, vars
komplexa impedans här betecknas med Z (se fig. J2.2). Vi har |
|
| Fig. J2.2 |
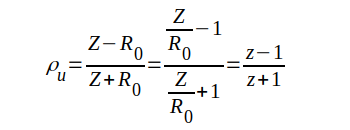 |
J2.2 |
där z = r + jx är det i föregående avsnitt introducerade komplexa impedanstalet. Vi löser ut z ur sambandet J2.2, inför ρu = u + jv och får
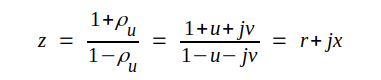 |
|
Separering av real- och imaginärdelar ger de båda sambanden
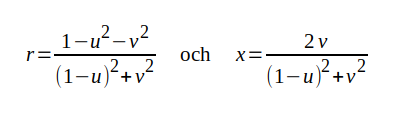 |
J2.3a J2.3b |
Ur sambandet J2.3a erhålles
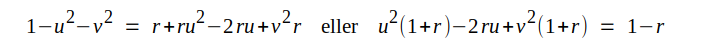 |
|
eller
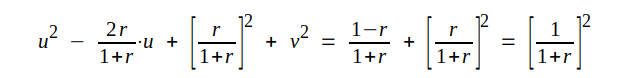 |
|
Uttrycket kan nu skrivas under den slutgiltiga formen
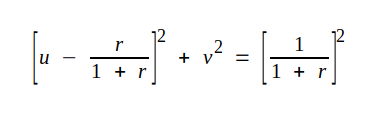 |
J2.4 |
Sambandet J2.4 representerar i ett u-v-koordinatsystem en cirkel med radien
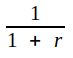 och medelpunkten i
och medelpunkten i 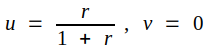 . Se härtill fig. J2.3, där cirklar
uppritas för r = 0, 0,5, 1, 2 och ∞ . Cirklar med r < 0 är ej
aktuella, om z skall vara ett fysikaliskt realiserbart
impedanstal.
. Se härtill fig. J2.3, där cirklar
uppritas för r = 0, 0,5, 1, 2 och ∞ . Cirklar med r < 0 är ej
aktuella, om z skall vara ett fysikaliskt realiserbart
impedanstal.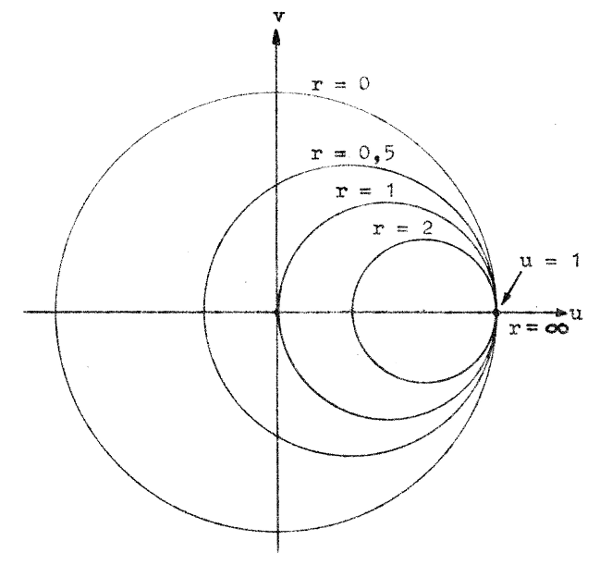 |
På analogt
sätt visar läsaren, att sambandet J2.3b kan skrivas
under formen
Sambandet J2.5 representerar i ett u-v-koordinatsystem en cirkel med radien 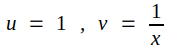 . I fig. J2.4
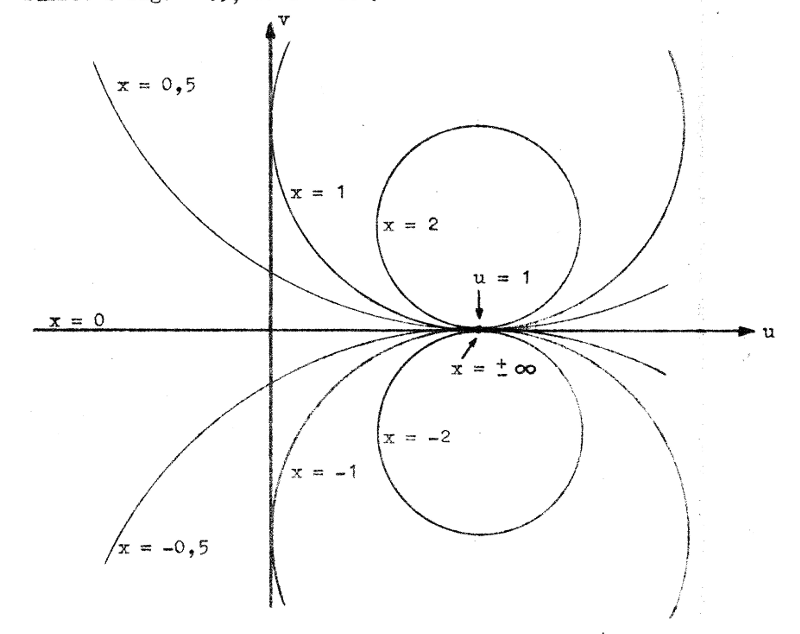
nedan har dylika cirklar ritats för x = 0, ±0,5, ±1, och
±2. . I fig. J2.4
nedan har dylika cirklar ritats för x = 0, ±0,5, ±1, och
±2. |
|||
| Fig. J2.3 |
För x = ±∞ övergår cirkeln i punkten u = 1, v = 0, något som även var fallet i fig. J2.3, då r = ∞.
| |
 |
|
| |
Fig. J2.4 | |
Lägger vi de båda cirkelskarorna (fig. J2.3 och J2.4) på varandra med sammanfallande axlar får vi ett diagram enligt fig. J2.5, där några cirklar
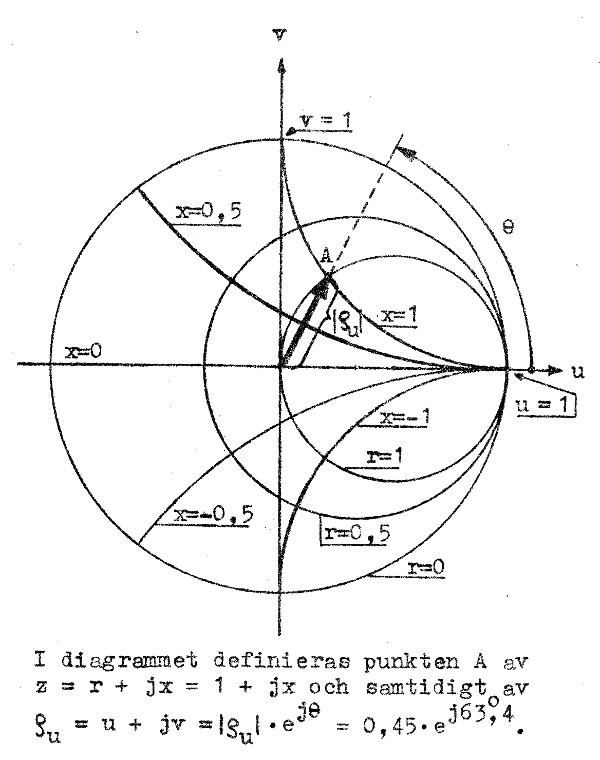 |
(r = 0, 0,5 och 1 samt x = 0,
±0,5 och ±1) utritats. Som förut påpekats måste alla
fysikaliskt realiserbara impedanstal ligga inom en
cirkel med radien 1 och medelpunkten i origo (cirkeln
för r = 0). Detta är orsaken till att diagrammet i fig.
J2.5 begränsas till att omfatta området innanför nämnda
cirkel. Är belastningens impedanstal känt (exempelvis z = 1 + j ; punkten A i diagrammet fig. J2.5), kan vi direkt i diagrammet avläsa den häremot svarande komplexa reflexionsfaktorn ρu, d.v.s. dess absolutbelopp │ρu│och fasvinkel θ. |
|
| Fig. J2.5 |
kan givetvis även gå den motsatta vägen och bestämma belastningens impedanstal z = r + jx, om │ρu│och θ är kända.
Vi kan, om vi så önskar, betrakta u-v-planet som ett komplext talplan med realaxel (u) och imaginäraxel (v), i vilket ρu-visaren åskådliggöres, varvid r- och x-cirklarna är ortkurvor för ρu-visarens spets, då r respektive x är konstant.
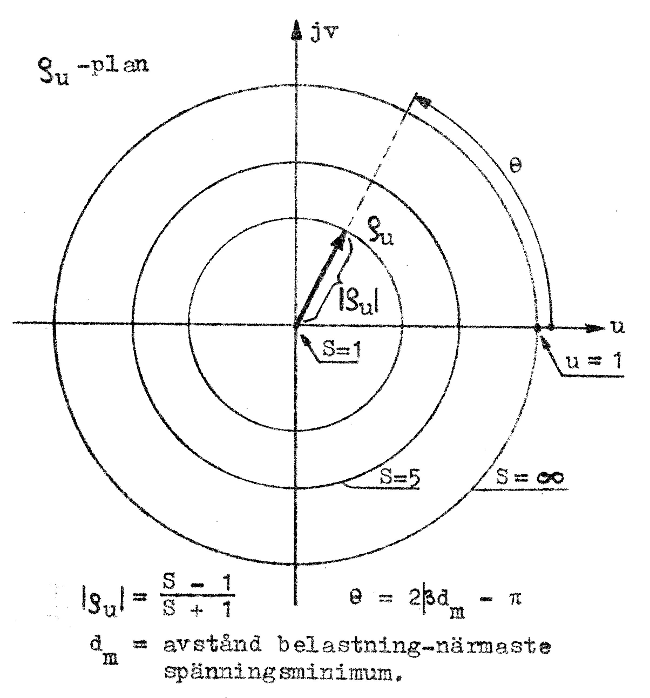
Enligt sambandet J1.120 är
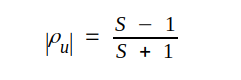 |
J2.6 |
och enligt sambandet J1.118b är
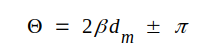 |
J2.7 |
om dm är avståndet mellan belastningen och närmaste spänningsminimum. I diagrammet fig. J2.6 har θ = 2βdm - π avsatts moturs från horisontalaxeln.
Varje diagrampunkt inom enhetscirkeln i fig. J2.5 motsvaras av ett värdepar (r, x) och varje värdepar inom enhetscirkeln i fig. J2.6 motsvaras av ett värdepar (S, βdm). Ritar vi det senare diagrammet på genomskinligt papper och lägger det ovanpå diagrammet enligt fig. J2.5 (sammanfallande koordinataxlar och samma radie på enhetscirklarna), så uppkommer ett dubbeldiagram, där varje diagrampunkt motsvarar två värdepar.
 |
Av uppmätta värden på S och βdm
(stående-våg-mätning) kan man alltså med hjälp av
dubbeldiagrammet utan räkning bestämma r och x hos
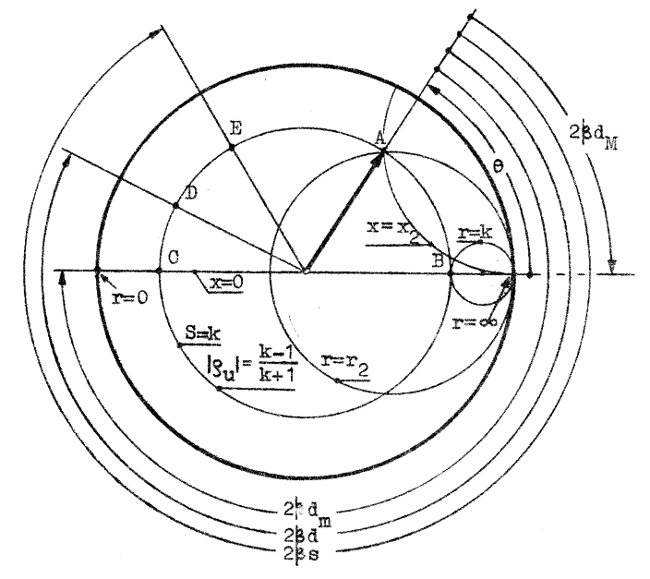
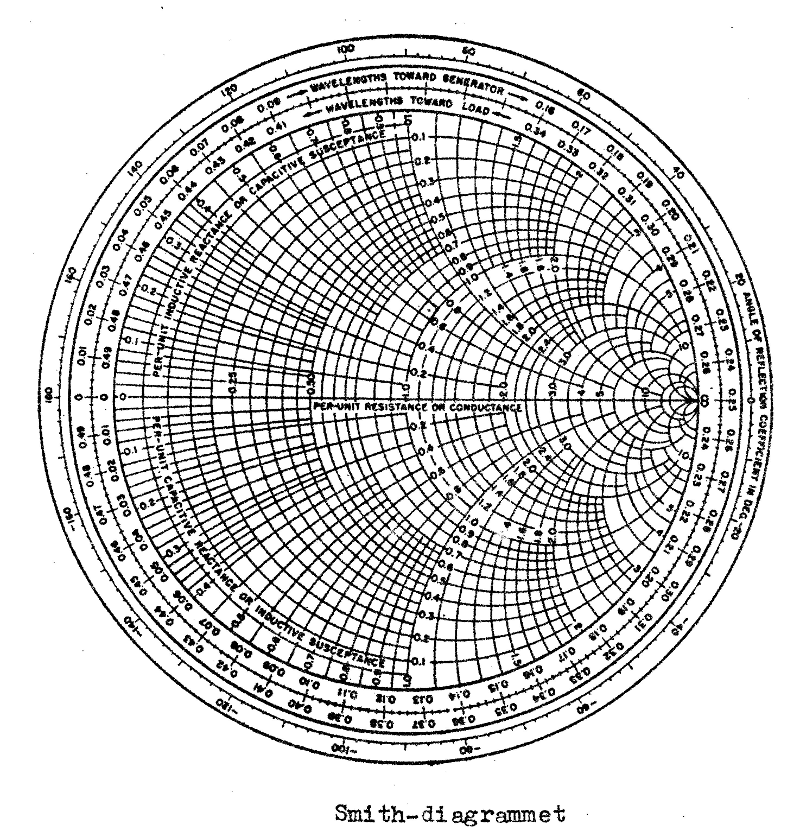
belastningen och vice versa. Övning: Visa att S-cirkeln för S = k (k = konstant) skär positiva u-axeln i samma punkt som r-cirkeln för r = k. Det ovan nämnda dubbeldiagrammet är det s.k. Smith-diagrammet. Cirklar för konstant S utritas dock ej, utan alla erforderliga S-cirklar (│ρu│- cirklar) |
|
| Fig. J2.6 |
ritar vi själva vid diagrammets användning. Ett praktiskt Smith-diagram brukar utformas i enlighet med fig. J2.9 (sid. J2.7).
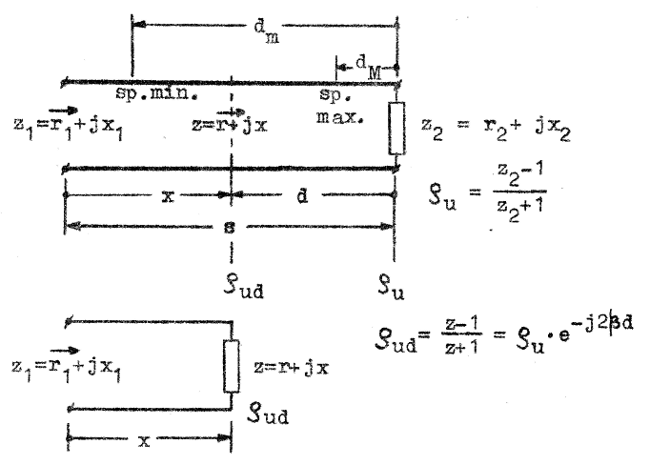 |
För att få
ytterligare insikt i Smith-diagrammets användning
studerar vi en med komplexa impedanstalet z2
= r2 + jx2 belastad förlustfri
ledning med längden s (s > 3/4⋅λ). Se härtill fig.
J2.7. Vi uppsöker först den mot z2 svarande punkten i Smith diagrammet (punkten |
|
| Fig. J2.7 |
A i fig. J2.8) Om diagrammets periferi är försedd med en vinkelskala (som i fig. J2.9) kan vi direkt avläsa reflexionsfaktorns fasvinkel θ.
 |
│ρu│ kan vi
bestämma genom att mäta ρu-visarens längd. I
fig. J2.8 är visarens längd 26,5 mm. Diagrammets radie
(r=0 cirkelsens radie) är 38,0 mm, varför vi får  Enligt sambandet J1.95 är komplexa reflexionsfaktorn på ett godtyckligt avstånd d från belastningen |
|
| Fig. J2.8 |
(γ = jβ i förlustfria fallet)
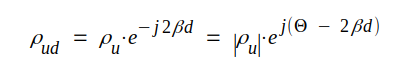 |
J2.8 |
ρud-visaren har samma längd som ρu-visaren, men den är vriden vinkeln 2βd medsols i förhållande till ρu-visaren (visarspetsen i punkten D i fig. J2.8). I punkten D får vi ett nytt värdepar (r, x), som ger det komplexa impedanstalet på ledningen på avståndet d från belastningen (se härtill även fig. J2.7). Fortsätter vi vridningen till punkten E (ledningsingången), kan vi i diagrammet direkt avläsa ledningens ingångsimpedanstal z1 = r1 + jx1.
Om vi från punkten A vrider visaren ett varv, har vi
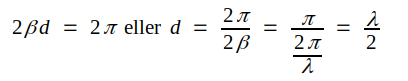 |
d.v.s. ett varvs vridning i diagrammet motsvarar en halv våglängds förflyttning på ledningen. Diagrammets periferi kan därför lämpligen förses med en våglängdsskala (jämför fig. J2.9, där vi har två våglängdsskalor, en graderad medsols och en motsols).
Vi har ovan konstaterat att medsols vridning i diagrammet motsvarar förflyttning på ledningen i riktning från belastningen mot generatorn. Detta har i diagrammet fig. J2.9 utmärkts med texten "wavelengths toward generator" (våglängder i riktning mot generatorn). Lägg även märke till texten "wavelength toward load" (våglängder i riktning mot belastningen).
 |
Under
medsols vridning från punkten A passerar visaren punkten
B i diagrammet. På ledningen har vi då förflyttat oss en
sträcka dM från belastningen. Sträckan
dM är avståndet mellan belastningen och
närmaste spänningsmaximum, ty i ett
spänningsmaximum är impedanstalet rent resistivt
och i diagrammet är x = 0 på horisontella axeln.
Att det är fråga om ett spänningsmaximum framgår av |
|
| Fig. J2.9 |
sambandet J1.125 (sid. J1.34), som utsäger, att impedansen i ett spänningsmaximum är S⋅R0, d.v.s. impedanstalet är resistivt och lika med S (S > 1). På högra delen av horisontella axeln (positiva u-axeln) är r > 1. Genom att i punkten B avläsa r-värdet (=k i fig. J2.8) får vi stående-våg-förhållandet ur sambandet r = S. (jämför övningsuppgiften på sid. J2.5).
När visaren passerar punkten C i diagrammet måste vi av liknande skäl befinna oss i en spänningsminimumpunkt på ledningen (avståndet dm från belastningen) och vi kan därför med ledning av sambandet J1.126 i punkten C avläsa r = 1/S. Enligt diagrammet är som väntat dm - dM = λ/4.
Har vi på ledningen (med stående-våg-mätare) bestämt storheterna S och dm, kan vi utgå från punkten C och vrida visaren vinkeln 2βdm (eller på diagrammets våglängsskala sträckan dm uttryckt i våglänger) "toward load". Vi hamnar då i punkten A och kan där avläsa belastningens impedanstal z2 = r2 + jx2 . Det torde vara uppenbart, att alla spänningsminima är likaberättigade referenspunkter (vid försummad dämpning). Vi behöver alltså ej välja det minimum, som ligger närmast belastningen, eftersom en halv våglängds (eller heltalmultipel därav) förflyttning längs ledningen återför oss till samma diagrampunkt. Även spänningsmaxima kan användas som referenspunkter, men av praktiska mättekniska skäl användes endast spänningsminima som referenspunkter.
Låt oss slutligen visa, att Smith-diagrammet i oförändrad form även gäller för admittanstal. Om en diagrampunkt definieras av komplexa impedanstalet z, så är motsvarande komplexa admittanstal
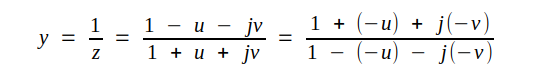 |
|
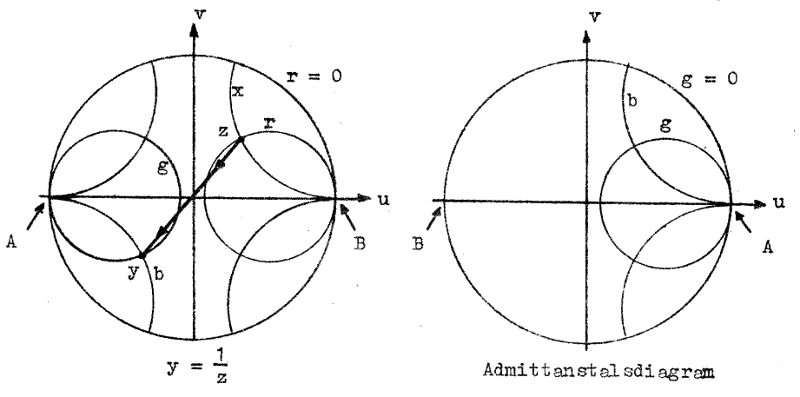
d.v.s. vi kan konstruera ett Smith-diagram för admittanstal genom att i det gamla diagrammet ändra tecken för såväl u som v. En dylik teckenändring sker, om alla diagrampunkter "speglas" i origo enligt fig. J2.10. Diagrammet blir så när som på parametrarna identiskt med det gamla.
| |
 |
|
| |
Konstruktion av Smith-diagrammet för admittanstal Fig. J2.10 |
|
I avsikt att utmärka Smith-diagrammets användning för såväl impedanstal som admittanstal har i fig. J2.9 r-skalan försetts med texten "per-unit resistance or conductance" (resistans- eller konduktanstal) och vidare har x-skalan försetts med texten "per-unit inductive reactance or capacitive susceptance" för positiva x-värden samt en motsvarande text för negativa axeln.
Övning: Beräkna med ledning av sambandet J1.81 (sid. J1.21) komplexa impedanstalet för en förlustfri ledning med längden λ/4. Ledningen är i fjärrändan belastad med komplexa impedanstalet z. Vilken anknytning har detta problem till fig. J2.10?
link >