< link link link >

    Riktig förståelse för (och även uppskattning av) Smith-diagrammet ernås bäst genom studium av ett antal konkreta exempel. I avsikt att härutinnan vara läsaren behjälplig ge nedan ett antal uppgifter med lösningar. Läsaren bör på egen hand med hjälp av diagramblad försöka lösa uppgifterna och först därefter studera  de givna lösningarna. Lösningarnas sifferdata har avlästs i ett normalt Smith-diagram (General Radio Company, Smith chart , form 756-N) med den avläsningsnoggranhet, som diagrammets skalor medger. De nedan ritade figurerna är principskisser, som ej gör anspråk på att var skalenliga.

Uppgift 1: I en koaxialledning med egenresistansen 50 ohm och längden 0,3 våglängder har man med stående-våg-meter bestämt SVF till 2,5 och ett spänningsminimum har lokaliserats till en punkt på avståndet 0,2 våglängder från belastningen. Sinus-emk.

1. Beräkna belastningens komplexa impedans.
2. Beräkna ledningens komplexa inimpedans.
3. Beräkna ledningens komplexa inadmittans.
4. Finns någon spänningsmaximumpunkt på ledningen?

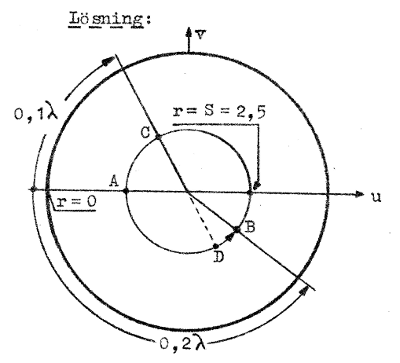		a) Vi ritar en cirkel med medelpunkten i origo och för S = 2,5, d.v.s. en cirkel, som går genom punkten r = S = 2,5 på horisontella axeln. Minimipunkten (r = 1/S) motsvarande punkten A. Vi går därifrån 0,2λ mot belastningen och hamnar i punkten B, där vi avläser impedanstalet z2 = 1,67 - j⋅1,02. Belastningsimpedansen blir alltså Z2 = R0⋅z2 = 50⋅(1,67 - j 1,02) = 83,5 - j51,0 ohm.
Fig. J2.11

b) Vi går från A 0,1λ (0,3λ - 0,2λ) mot generatorn och avläser i punkten C z₁ = 0,57 + j0.57, d.v.s. inimpedansen blir Z₁ = 50(0,57+j0.57) = 28,5 + j28,5 ohm.
c) Vi går till den till C diametralt motsatta punkten D och avläser y₁ = 1/z₁ = 0,88 - j0.88 och får Y₁ = G₀⋅y₁ = 1/R₀⋅y₁ = 1/50(0,88 - j0.88) = 17,6 - j17,6 mS.
d) Vid gång från A till B respektive från A till C passerar vi ej horisontella axelns högra del (r >0), varav vi drar slutsatsen att någon spänningsmaximipunkt (i gängse bemärkelse) ej finns på ledningen (däremot har spänningens effektivvärde ett maximum. Var?). Ledningen måste ha en utsträckning av minst 0,25λ åt endera hållet från minimipunkten räknat, om ett spänningsmaximum skall finnas. Varför?

Uppgift 2: Ett komplext tal Z = 20 + j30 är givet. Beräkna det komplexa talet Y = 1/Z.

    Lösning: Betrakta Z som en impedans och normera med avseende på t.ex. 10 ohm, så att  får för diagrambruk lämplig storleksordning. Gå i diagrammet in i punkten r = 2 och x = 3. Gå sedan till den diametralt motsatta punkten och avläs . Övergång till admittans ger

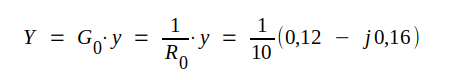d.v.s.

slutresultat


Uppgift 3: Komplexa inimpedansen på en ledning med egenresistansen 100 ohm är Z₁ = 300 + j400 ohm. Ledningen är 1 1/8 våglängd lång.

    a) Bestäm komplexa reflexionsfaktorn vid belastningen.
    b) Beräkna SVF på ledningen.
    c) Skissera spänningsfördelningen (effektivvärderfördelningen) på ledningen.

		a) Vi normerar Z1 och får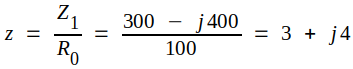 som i diagrammet representeras av punkten A (r = 3, x = 4). Från A går vi λ/8 = 0,125λ (= ett kvarts varv i diagrammet; egentligen 1 1/8, d.v.s. 2 hela varv + 1/4 varv) i riktning mot belastningen till punkten B, där belastningens impedanstal kan avläsas, om så önskas. Vi mäter sträckan 0B (=0A) och får 24,0 mm. Vi mäter också sträckan 0D och
Fig. J2.12

får 30,5 mm (diagrammet är i detta fall ritat i skala), vilket ger


    Reflextionskoefficienternas fasvinkel θ avläses på vinkelskalan i enlighet med fig. J2.12. Vi får θ = 108,4°, d.v.s.


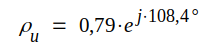b) SVF avläses i punkten C, där vi har r = S ≈ 8,5. Punkten C ger i detta fall dålig avläsningsnoggrannhet för S. Vi kan i stället gå till punkten E, där vi avläser R = 1/S = 0,116, d.v.s.

=============

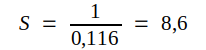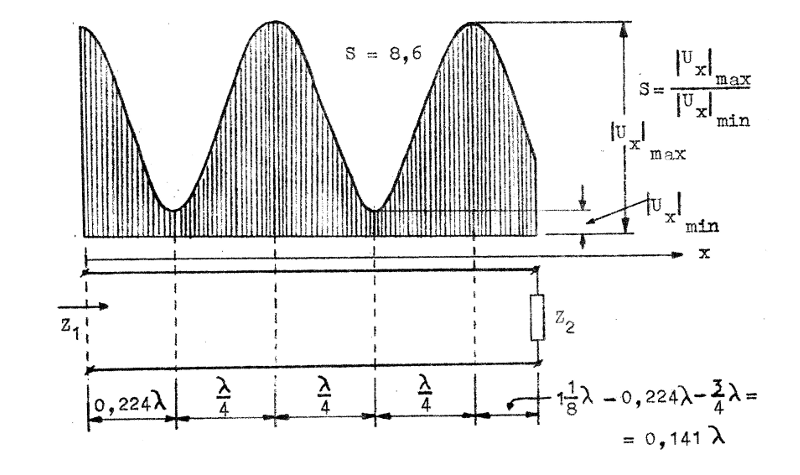
c) Från punkten A (ledningsingången) går vi mot belastningen (motsols) och når punkten E (spänningsminimum). På diagrammets våglängdsskala innebär detta en förflyttning av 0,224λ. Efter ytterligare ett halvt varv (λ/4) når vi punkten C (spänningsmaximum). Dessa informationer jämte SVF (S = 8,6 enligt uppgiftens b-del) är tillräckliga för skissen i fig. J2.13 nedan.

	Fig. J2.13

    Fig. J2.13 är en skiss i den bemärkelsen, att vi inte känner spänningsfördelningskurvans exakta form. Vi vet endast att maximivärdet förhåller sig till minivärdet som 8,6 : 1. Den lätthet med vilken en dylik skiss kan göras är i många fall av stort värde.

    Därmed är uppgift 3 slutbehandlad.

Uppgift 4: På en fölustfri transmissionsledning, som i fjärrändan är belastad med en viss impedans, har man uppmätt stående-våg-förhållandet S = 4,0. Vidare har man uppmätt avståndet mellan två närliggande spänningsminima till 25,0 cm. Ett spänningsminimum inträffade 28,0 cm från belastningen. Bestäm längd och läge (avstånd från belastningen) för en med ledningen parallellkopplad, kortsluten reaktansgren, som går ledningen anpassad. Reaktansgrenen göres så kort som möjligt och placeras så nära belastningen som möjligt. Se härtill sid. J1.39-41 (engrensanpassaren).

		Lösning: Vi noterar först, att λ = 50 cm, eftersom avståndet mellan två närliggande spänningsminima är 25 cm (λ/2), vilket vidare innebär, att ett spänningsminimum inträffar 28/50⋅λ = 0,56λ från belastningen. Ett spänningsminimum inträffar tydligen också på avståndet dm = 0,56λ - 0,5λ= 0,06λ.     Eftersom vi i denna uppgift arbetar med parallellkopplade ledningar, kan vi allmänt säga, att det är lämpligt att arbeta med admittanstal och ej med impedanstal
Fig. J2.14

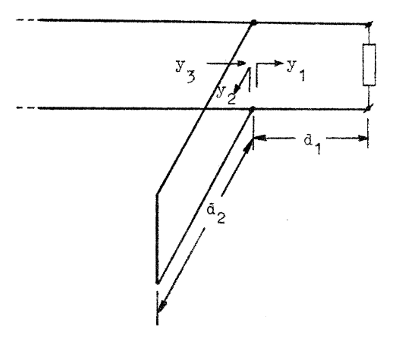
		I fig. J2.14 är y1 det komplexa admittanstal, vi ser i riktning mot belastningen omedelbart till höger om grenpunkten. y2 är det komplexa (imaginära) admittanstal, vi ser in på reaktansgrenen omedelbart hitom grenpunkten. y3 är på analogt sätt komplexa admittanstalet omedelbart till vänster om grenpunkten d.v.s. y3 = y1 + y2 För anpassning fordras att y3 = 1 + j⋅0. Eftersom y2 är rent susceptivt (helt förlustfri ledningssektion), måste vi ha
Fig. J2.15

y₁ = 1 + jb₁ där b₁ är ett vist susceptanstal.

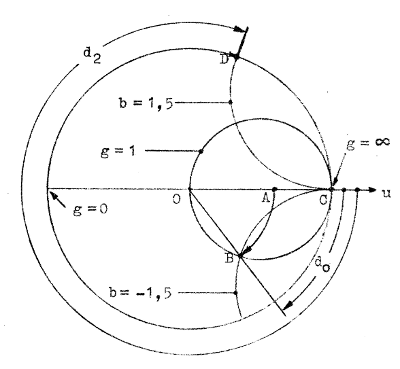
    I admittansdiagrammet fig. J2.15 utgår vi från punkten A (spänningsminimipunkten). I en dylik är r = 1/S, d.v.s. g = 1/r = S. Punkten A kännetecknas alltså av g = S och b = 0.

    Från A går vi i riktning mot generatorn till punkten B (som ligger på g = 1 cirkeln), där vi avläser y₁ = 1 + jb₁ = 1 - j1,5, d.v.s. b₁=-1,5. På diagrammets våglängdsskala avläser vi förflyttningen från minimipunkten d₀ = 0.074λ. Avståndet mellan belastningen och närmaste spänningsminimum har vi tidigare bestämt till d_m = 0,06λ, d.v.s.

    d₁ = d_m + d₀ = 0,074λ + 0,06λ = 0.134λ = 0,134⋅50 cm = 6,7 cm

    Därmed är längden d1 bestämd.  Det bör anmärkas, att vi från punkten A kunde nått g = 1 cirkeln genom att gå mot belastningen. För att nå cirkeln måste vi gå 0,074λ men redan efter att ha gått 0,06λ stöter vi på belastningen. Det ovannämda d₁-värdet är sålunda det enda som uppfyller uppgiftens krav (så litet d₁ som möjligt).

    Eftersom y₂ = y₃ - y₁ får vi y₂ = 1 - 1 + j1,5 = j1,5.

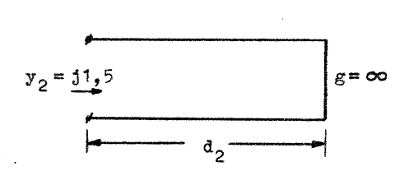
    Bestämning av längden d₂ behandlar vi som ett separat problem. Se härtill fig. J2.16. Vi utgår från g = ∞ (punkten C) och rör oss längs diagrammets periferi i riktning mot generatorn, tills vi i punkten D avläser b = 1,5 . På diagrammets längdskala avläser vi

                    d₂ = 0,406λ = 0,406⋅50 cm = 20,3 cm

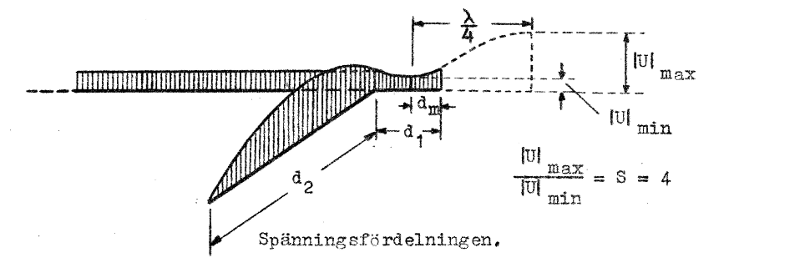
		Att d2 = 20,3 cm är den kortaste kortslutna reaktansgrenen torde vara uppenbart. Skulle en öppen reaktansgren kunnat göras kortare?     Med ledning av givna och beräknade data skisseras som avslutning spänningsfördelningen (amplitudfördelningen) på ledningssystemet (fig. J2.17)
Fig. J2.16

	Fig. J2.17

    Som avslutande uppgift ges följande relativt svåra uppgift, vars lösning läsaren bör söka utforma på egen hand.

Uppgift 5: En tvågrensanpassare enligt fig. J1.34 (sid. J1.41) har längden d₀ = λ/4. Avståndet mellan belastningen och den närmaste grenpunkten är λ/8. Belastningens komplexa impedanstal är z₂ = Z₂/R₀ = 2 + j3. Bestäm erforderliga längder d₁ och d₂.

Dessa längder väljes så korta som möjligt.

Svar: d₁ = 0,074λ , d₂ = 0,125λ .


link >