Smith-diagrammets användning har i föregående avsnitt demonstrerats på förlustfria ledningar. I praktiken använder vi samma metodik för ledningar med små förluster. I fråga om långa ledningar kan det dock vara nödvändigt att beakta dämpningens inverkan.
Enligt sambandet J1.95 (sid. J1.24) gäller
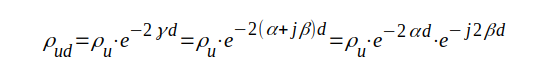 |
|
där ρud = komplexa reflexionsfaktorn på avståndet d från belastningen,
ρu = komplexa reflexionsfaktorn vid belastningen.
Vid förflyttning från belastningen i riktning mot generatorn (d ökar) rör sig reflexionsfaktorns visarspets medsols i Smith-diagrammet samtidigt som visarens längd │ρud│ avtar på grund av exponentialfaktorn e-2αd. Visarspetsen rör sig sålunda i spiral och efter tillräckligt många varvs vridning hamnar spetsen i Smith-diagrammets origo, vilket uttrycker, att inimpedanstalet på en oändligt lång ledning är 1 (Zin = R0).
Låt oss exemplifiera med följande uppgift.
Uppgift: En ledning med längden 20,2 våglängder är i fjärrändan belastad med komplexa impedanstalet z2 = 1,2 + j1,6. Ledningens
dämpning är α = 0,5 dB/m. Generatorfrekvensen är 3 GHz. Bestäm komplexa impedanstalet i generatorändan.
Lösning: Vi beräknar först våglängden på ledningen och får
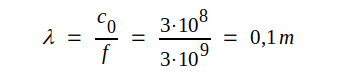 |
|
Med ledningslängden d = 20,2λ = 20,2⋅0,1 = 2,02 m blir ledningens totala dämpning
α⋅d = 0,5 ⋅ 2,02 = 1,01 dB = 1,01 ⋅ 0,115 = 0,116 N
Exponentialfaktorn får värdet
e-2αd = e-2⋅0,116 = e-0,232 = 0.793
I Smith-diagrammet startar vi i punkten A, som svarar mot belastningen (r=1,2 , x=1,6) och går därefter längs en S-cirkel 0,2λ (egentligen 20,2λ) i riktning mot generatorn. Vi hamnar då i punkten B,
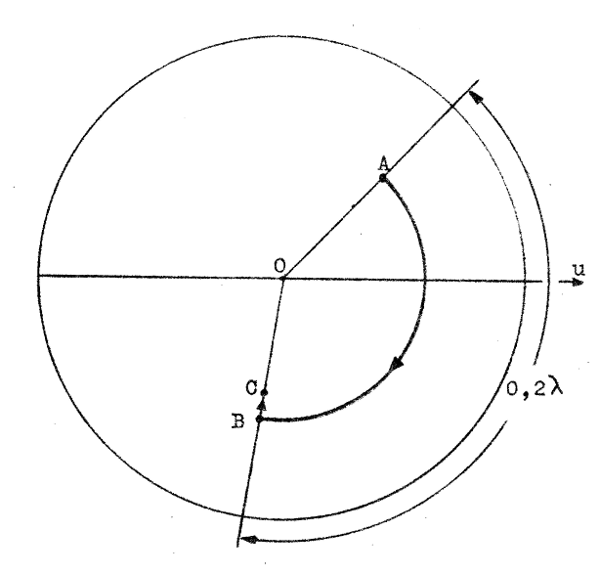 |
där vi avläser r = 0,44 och
x=-0,78, d.v.s. ledningens inimpedanstal är, om
dämpningen försummas, lika med z'in = 0,44 - j0,78 Vi uppmäter sträckan OA (som är proportionell mot │ρud│= │ρu│⋅ e-2αd = │ρu│⋅ 0.793 avsätter vi sträckan OC = 54⋅0.793 = 43 mm och får på så sätt punkten C (ledningens inklämmor), där vi |
|
| Fig. J2.18 |
avläser r = 0,58 och x = -0,69, d.v.s. inimpedanstalet med dämpning är
zin = 0,58 - j0,69
Från punkten A till punkten C rör vi oss egentligen längs en spiral, som uppkommer, då visaren OA med sakta avtagande längd vrides medsols 2⋅20,2 varv i diagrammet.
Övning: Komplexa inimpedansen på en viss ledning med längden 20 våglängder är zin = 25 ohm. Ledningens egenresistans är R0 = 50 ohm och dess dämpningskonstant är α = 0,5 dB/m. Frekvensen är 3 GHz. Bestäm belastningsimpedansens real- och imaginärdel.
När dämpningskonstanten är stor, när ledningsänden är stor eller när båda är stora, dämpas såväl den framgående som den reflekterade vågen i så hög grad, att SVF ändrar sig avsevärt längs ledningen. Talar vi i dessa fall om SVF eller reflexionsfaktorn, menar vi värdena i belastningens omedelbara närhet. Vi bör också ihågkomma, att stor dämpningskonstant medför, att egenimpedansen ej längre blir rent resistiv. Vid höga frekvenser dominerar dock egenimpedansens reella del.
link >